ความรู้เบื้องต้นเกี่ยวกับการแจกแจงแบบทวินาม

การแจกแจงแบบทวินาม เป็นหนึ่งในการแจกแจงที่ได้รับความนิยมมากที่สุดในสถิติ เพื่อให้เข้าใจถึงการแจกแจงแบบทวินาม ก่อนอื่นให้เข้าใจ การทดลองทวินาม ก่อน

การทดลองทวินาม

การทดลองทวินาม คือการทดลองที่มีคุณสมบัติดังต่อไปนี้:

• การทดลองประกอบด้วยการทดลองซ้ำ n ครั้ง
• การทดลองแต่ละครั้งมีเพียงสองผลลัพธ์ที่เป็นไปได้
• ความน่าจะเป็นที่จะสำเร็จ ซึ่งแสดงโดย p จะเท่ากันสำหรับการทดลองแต่ละครั้ง
• การทดสอบแต่ละครั้งมีความเป็นอิสระ

ตัวอย่างที่ชัดเจนที่สุดของการทดลองทวินามคือการโยนเหรียญ เช่น สมมติว่าเราพลิกเหรียญ 10 ครั้ง นี่เป็นการทดลองทวินามเนื่องจากมีคุณสมบัติสี่ประการดังต่อไปนี้:

• การทดลองประกอบด้วยการทดลองซ้ำ n ครั้ง มีการทดลองทั้งหมด 10 ครั้ง
• การทดลองแต่ละครั้งมีเพียงสองผลลัพธ์ที่เป็นไปได้: หัวหรือก้อย
• ความน่าจะเป็นที่จะสำเร็จ ซึ่งแสดงโดย p จะเท่ากันสำหรับการทดลองแต่ละครั้ง หากเรากำหนดให้ “ความสำเร็จ” เป็นจุดเริ่มต้น ความน่าจะเป็นที่จะประสบความสำเร็จคือ 0.5 อย่างแน่นอนสำหรับการทดลองแต่ละครั้ง
• การทดลองแต่ละครั้งมีความเป็นอิสระ – ผลของการโยนเหรียญหนึ่งครั้งจะไม่ส่งผลต่อผลลัพธ์ของการโยนเหรียญอื่นๆ

การแจกแจงแบบทวินาม

การแจกแจงแบบทวินาม อธิบายถึงความน่าจะเป็นที่จะประสบความสำเร็จ k ครั้งในการทดลองทวินาม n ครั้ง

หาก ตัวแปรสุ่ม X เป็นไปตามการแจกแจงแบบทวินาม ความน่าจะเป็นที่ X = k สำเร็จจะพบได้จากสูตรต่อไปนี้:

P(X=k) = _n C _k * p ^k * (1-p) ^nk

ทอง:

• n: จำนวนการทดลอง
• k: จำนวนความสำเร็จ
• p: ความน่าจะเป็นที่จะประสบความสำเร็จในการทดลองที่กำหนด
• _n C _k : จำนวนวิธีในการได้รับ k ความสำเร็จในการทดลอง n ครั้ง

เช่น สมมุติว่าเราโยนเหรียญ 3 ครั้ง เราสามารถใช้สูตรด้านบนเพื่อกำหนดความน่าจะเป็นที่จะได้หัว 0, 1, 2 และ 3 ในการทอยทั้ง 3 ครั้ง:

P(X=0) = ₃ C ₀ * 0.5 ⁰ * (1-0.5) ^3-0 = 1 * 1 * (0.5) ³ = 0.125

ป(X=1) = ₃ ค ₁ * 0.5 ¹ * (1-0.5) ^3-1 = 3 * 0.5 * (0.5) ² = 0.375

P(X=2) = ₃ C ₂ * 0.5 ² * (1-0.5) ^3-2 = 3 * 0.25 * (0.5) ¹ = 0.375

ป(X=3) = ₃ ค ₃ * 0.5 ³ * (1-0.5) ^3-3 = 1 * 0.125 * (0.5) ⁰ = 0.125

หมายเหตุ : เราใช้ เครื่องคิดเลขแบบรวม นี้เพื่อคำนวณ _{nCk สำหรับ} แต่ละตัวอย่าง

เราสามารถสร้างฮิสโตแกรมง่ายๆ เพื่อให้เห็นภาพการแจกแจงความน่าจะเป็นได้:

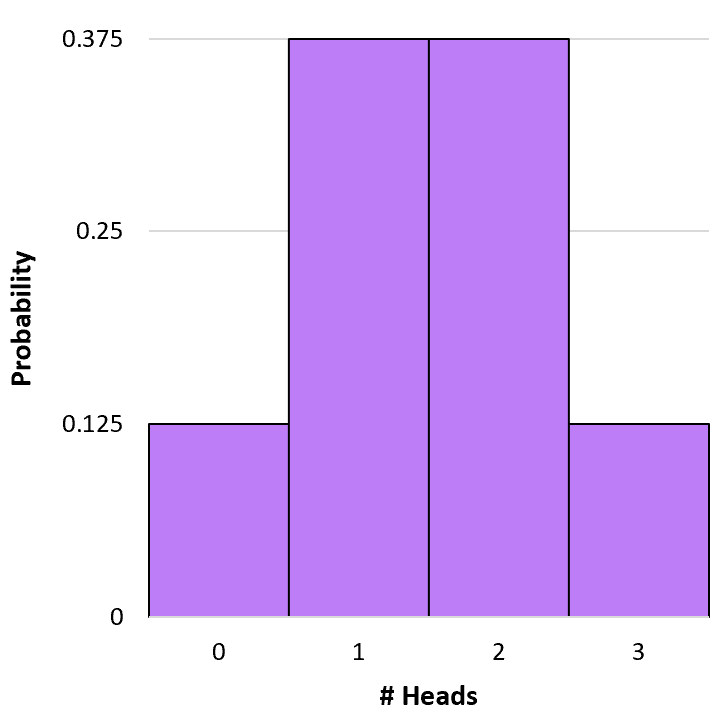
การคำนวณความน่าจะเป็นแบบทวินามสะสม

การคำนวณความน่าจะเป็นแบบทวินามเดี่ยวเป็นเรื่องง่าย (เช่น ความน่าจะเป็นที่เหรียญจะออกหัว 1 ครั้งจากการโยน 3 ครั้ง) โดยใช้สูตรข้างต้น แต่ในการคำนวณความน่าจะเป็นแบบทวินามสะสม เราจำเป็นต้องเพิ่มความน่าจะเป็นแต่ละรายการ

ตัวอย่างเช่น สมมติว่าเราต้องการทราบความน่าจะเป็นที่เหรียญจะขึ้นหัว 1 ครั้งหรือน้อยกว่าจากการเสี่ยง 3 ครั้ง เราจะใช้สูตรต่อไปนี้เพื่อคำนวณความน่าจะเป็นนี้:

P(X≤1) = P(X=0) + P(X=1) = 0.125 + 0.375 = 0.5 .

สิ่งนี้เรียก ว่าความน่าจะเป็นสะสม เนื่องจากเกี่ยวข้องกับการบวกความน่าจะเป็นหลายรายการ เราสามารถคำนวณความน่าจะเป็นสะสมที่จะได้ k หัวหรือน้อยกว่าสำหรับแต่ละผลลัพธ์โดยใช้สูตรที่คล้ายกัน:

ป(X≤0) = ป(X=0) = 0.125 .

P(X≤1) = P(X=0) + P(X=1) = 0.125 + 0.375 = 0.5 .

P(X≤2) = P(X=0) + P(X=1) + P(X=2) = 0.125 + 0.375 + 0.375 = 0.875 .

P(X≤3) = P(X=0) + P(X=1) + P(X=2) + P(X=3) = 0.125 + 0.375 + 0.375 + 0.125 = 1 .

เราสามารถสร้างฮิสโตแกรมเพื่อแสดงภาพการแจกแจงความน่าจะเป็นสะสมได้:

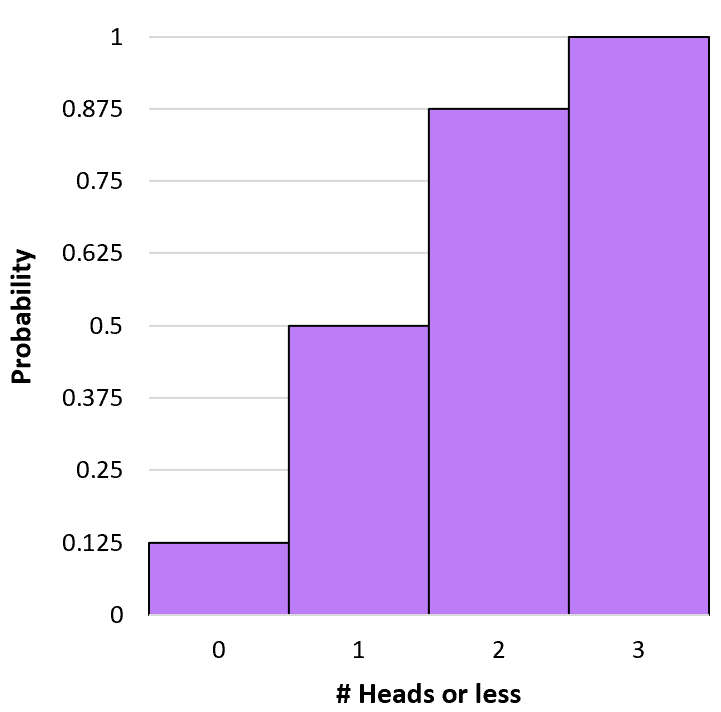
เครื่องคำนวณความน่าจะเป็นแบบทวินาม

เมื่อเราทำงานกับตัวเลขเล็กๆ (เช่น การโยนเหรียญ 3 เหรียญ) ก็สมเหตุสมผลที่จะคำนวณความน่าจะเป็นแบบทวินามด้วยมือ อย่างไรก็ตาม เมื่อเราทำงานกับตัวเลขที่มากขึ้น (เช่น 100 งวด) การคำนวณความน่าจะเป็นด้วยมืออาจเป็นเรื่องยาก ในกรณีเหล่านี้ การใช้ เครื่องคำนวณความน่าจะเป็นแบบทวินาม แบบที่แสดงด้านล่างอาจเป็นประโยชน์

ตัวอย่างเช่น สมมติว่าเราโยนเหรียญ n = 100 ครั้ง ความน่าจะเป็นที่เหรียญจะตกหัวในการทดลองที่กำหนดคือ p = 0.5 และเราต้องการทราบความน่าจะเป็นที่เหรียญจะตกหัว k = 43 ครั้งหรือน้อยกว่า:

ต่อไปนี้เป็นวิธีการตีความผลลัพธ์:

• ความน่าจะเป็นที่เหรียญจะขึ้นหัว 43 เท่าพอดีคือ 0.03007
• ความน่าจะเป็นที่เหรียญจะขึ้นหัวน้อยกว่า 43 เท่า คือ 0.06661
• ความน่าจะเป็นที่เหรียญจะขึ้นหัว 43 ครั้งหรือน้อยกว่าคือ 0.09667
• ความน่าจะเป็นที่เหรียญจะขึ้นหัวมากกว่า 43 ครั้ง คือ 0.90333
• ความน่าจะเป็นที่เหรียญจะขึ้นหัว 43 ครั้งขึ้นไป คือ 0.93339

คุณสมบัติของการแจกแจงแบบทวินาม

การแจกแจงทวินามมีคุณสมบัติดังต่อไปนี้:

ค่าเฉลี่ยของการแจกแจงคือ μ = np

ความแปรปรวนของการแจกแจงคือ σ ² = np(1-p)

ค่าเบี่ยงเบนมาตรฐานของการแจกแจงคือ σ = √ np(1-p)

เช่น สมมุติเราโยนเหรียญ 3 ครั้ง ให้ p = ความน่าจะเป็นที่เหรียญตกหัว

จำนวนหัวเฉลี่ยที่เราคาดหวังคือ μ = np = 3*.5 = 1.5

ความแปรปรวนจำนวนหัวที่เราคาดหวังคือ σ ² = np(1-p) = 3*.5*(1-.5) = 0.75

ปัญหาการปฏิบัติการแจกแจงแบบทวินาม

ใช้แบบฝึกหัดแก้ปัญหาต่อไปนี้เพื่อทดสอบความรู้เกี่ยวกับการแจกแจงแบบทวินาม

ปัญหาที่ 1

คำถาม: บ็อบพยายามโยนโทษ 60% ถ้าเขาโยนโทษ 12 ครั้ง ความน่าจะเป็นที่เขาโยนโทษได้ 10 ครั้งพอดีเป็นเท่าใด?

คำตอบ: เมื่อใช้เครื่องคำนวณการแจกแจงแบบทวินามข้างต้นโดยมีค่า p = 0.6, n = 12 และ k = 10 เราจะพบว่า P(X=10) = 0.06385

ปัญหาที่ 2

คำถาม: เจสสิก้าโยนเหรียญ 5 ครั้ง ความน่าจะเป็นที่เหรียญจะขึ้นหัว 2 เท่าหรือน้อยกว่านั้นเป็นเท่าใด?

คำตอบ: เมื่อใช้เครื่องคำนวณการแจกแจงแบบทวินามข้างต้นด้วย p = 0.5, n = 5 และ k = 2 เราจะพบว่า P(X≤2) = 0.5

ปัญหา 3

คำถาม: ความน่าจะเป็นที่นักเรียนคนใดคนหนึ่งจะได้รับการตอบรับเข้าศึกษาในวิทยาลัยแห่งใดแห่งหนึ่งคือ 0.2 ถ้าสมัคร 10 คน ความน่าจะเป็นที่มากกว่า 4 คนจะได้รับการยอมรับเป็นเท่าใด

คำตอบ: การใช้เครื่องคำนวณการแจกแจงแบบทวินามข้างต้นด้วย p = 0.2, n = 10 และ k = 4 เราพบว่า P(X>4) = 0.03279

ปัญหาที่ 4

คำถาม: คุณพลิกเหรียญ 12 ครั้ง จำนวนหัวเฉลี่ยที่คาดหวังที่จะปรากฏคือเท่าใด?

คำตอบ: จำไว้ว่าค่าเฉลี่ยของการแจกแจงแบบทวินามคำนวณเป็น μ = np ดังนั้น μ = 12*0.5 = 6 หัว

ปัญหาที่ 5

คำถาม: มาร์คตีโฮมรันได้ 10% ของความพยายามของเขา หากเขาตีได้ 5 ครั้งในเกมที่กำหนด ความแปรปรวนของจำนวนโฮมรันที่เขาตีได้เป็นเท่าใด

คำตอบ: จำไว้ว่าความแปรปรวนของการแจกแจงแบบทวินามคำนวณได้เป็น σ ² = np(1-p) ดังนั้น ^σ2 = 6*.1*(1-.1) = 0.54

แหล่งข้อมูลเพิ่มเติม

บทความต่อไปนี้ช่วยให้คุณเรียนรู้วิธีใช้การแจกแจงแบบทวินามในซอฟต์แวร์ทางสถิติต่างๆ:

• วิธีการคำนวณความน่าจะเป็นแบบทวินามใน Excel
• วิธีการคำนวณความน่าจะเป็นแบบทวินามบนเครื่องคิดเลข TI-84
• วิธีการคำนวณความน่าจะเป็นแบบทวินามใน R
• วิธีการพล็อตการแจกแจงแบบทวินามใน R