ความโด่งสามารถเป็นลบได้หรือไม่?

ในสถิติ ความโด่ง ใช้เพื่ออธิบายรูปร่างของการแจกแจงความน่าจะเป็น

โดยเฉพาะอย่างยิ่งมันบอกเราว่าค่าข้อมูลคลัสเตอร์ในส่วนท้ายหรือด้านบนสุดของการแจกแจงดีเพียงใด

ความโด่งของการแจกแจงอาจเป็นค่าลบ ศูนย์ หรือบวกก็ได้

ซีโร่เคอร์โทซิส

หากการแจกแจงมีความโด่งเป็น 0 มันจะเท่ากับการแจกแจงแบบปกติซึ่งมีรูปร่างระฆังดังต่อไปนี้:

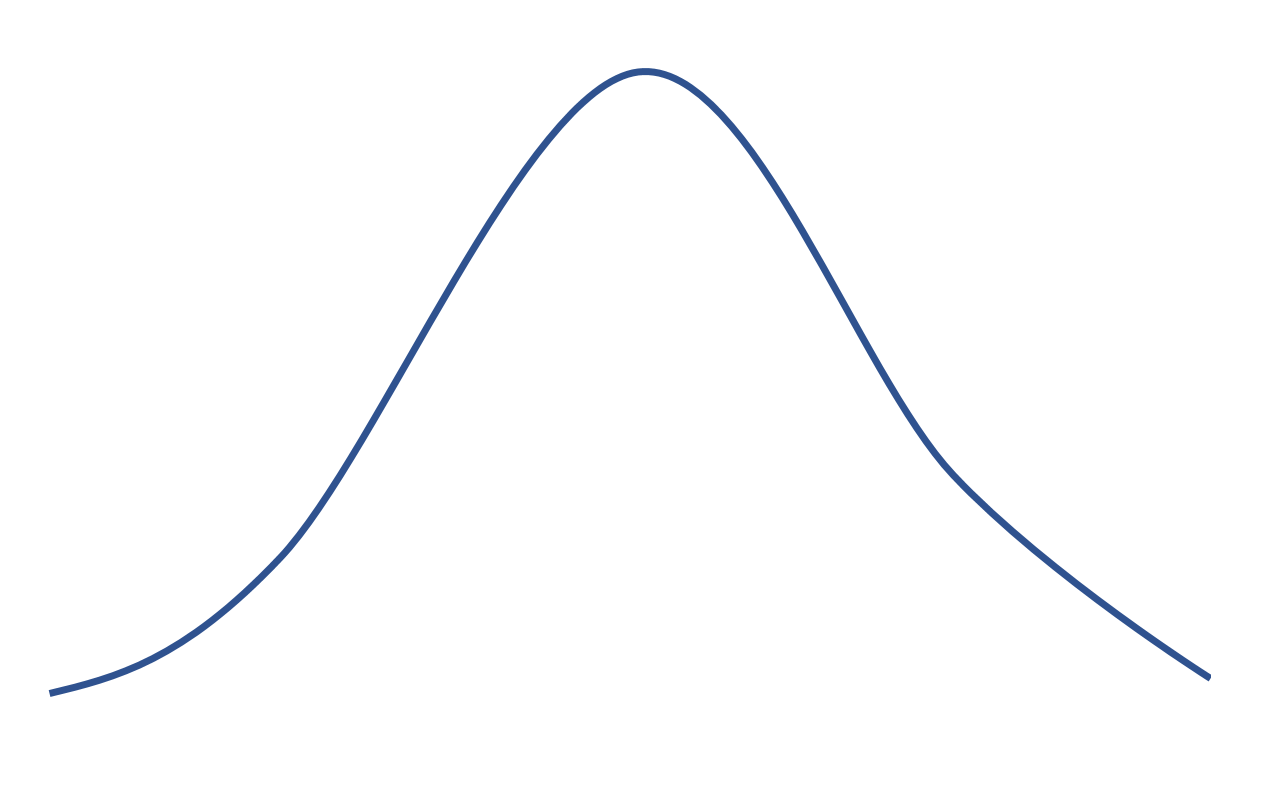
ความโด่งเชิงบวก

หากการกระจายตัวมีความโด่งเป็นบวก จะเรียกว่า Leptokurtic ซึ่งหมายความว่ามียอดที่แหลมกว่าและหางที่หนักกว่าเมื่อเทียบกับการกระจายแบบปกติ

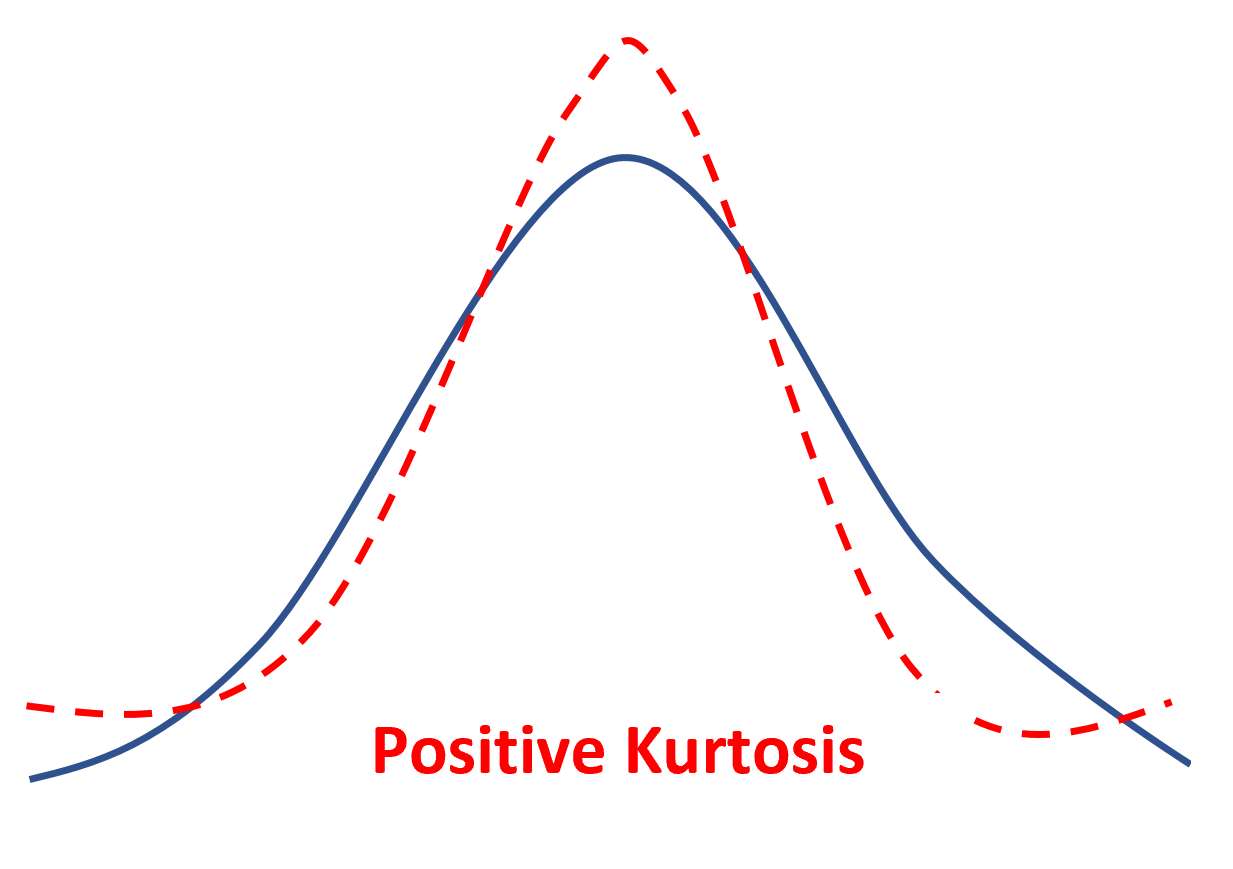
ซึ่งหมายความว่าค่าข้อมูลน้อยลงจะอยู่ใกล้กับค่าเฉลี่ยและค่าข้อมูลจะอยู่ที่ส่วนท้ายมากขึ้น

การกระจายตัวที่รู้จักกันดีที่สุดที่มีความโด่งเป็นบวกคือการกระจายแบบ t ซึ่งมียอดแหลมกว่าและหางที่หนักกว่าเมื่อเทียบกับการกระจายแบบปกติ

ความโด่งเชิงลบ

หากการกระจายตัวมีความโด่งเป็นลบ จะเรียกว่า platykurtic ซึ่งหมายความว่ามียอดแบนกว่าและหางบางกว่าเมื่อเทียบกับการกระจายแบบปกติ

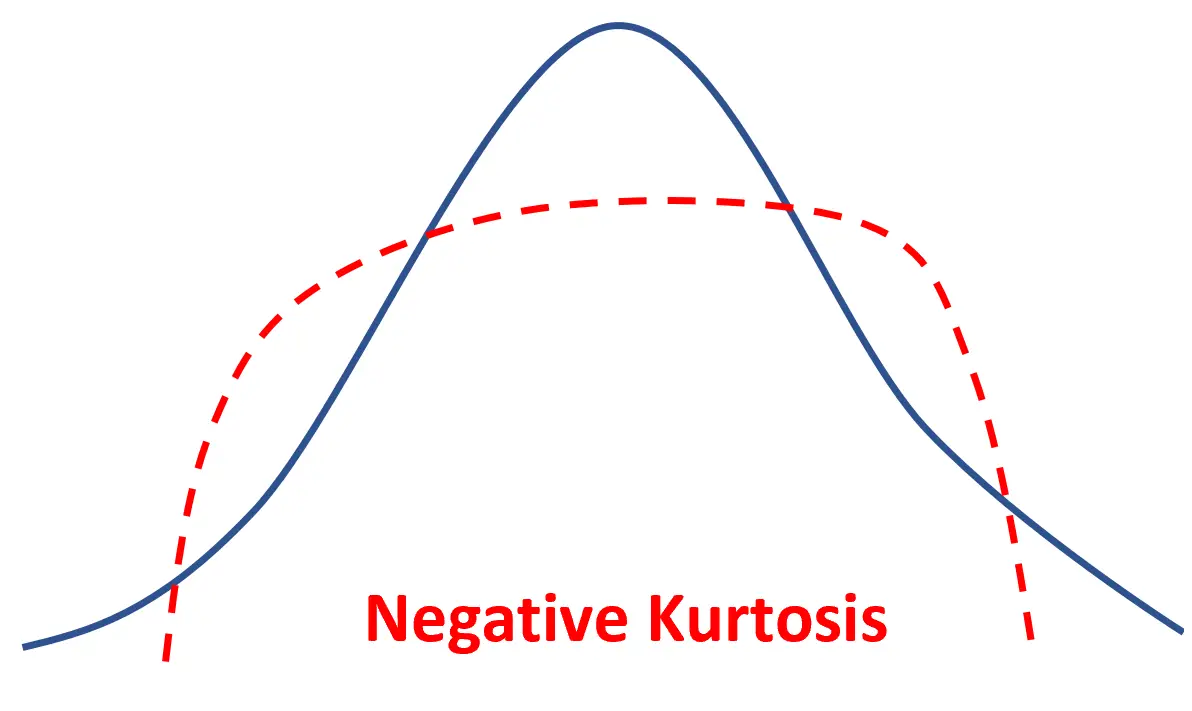
ซึ่งหมายความว่าค่าข้อมูลที่มากขึ้นจะอยู่ใกล้กับค่าเฉลี่ยและค่าข้อมูลที่น้อยลงจะอยู่ที่ส่วนท้าย

ตัวอย่างสุดโต่งของการกระจายตัวที่มีความโด่งเป็นลบคือ การกระจายตัวแบบสม่ำเสมอ ซึ่งไม่มียอดและเป็นการกระจายแบบแบนโดยสมบูรณ์

เมื่อใดจึงควรใช้การประจบสอพลอในทางปฏิบัติ

ในทางปฏิบัติ เรามักจะวัด ความโด่ง ของการกระจายตัวในขั้นตอนการวิเคราะห์เชิงสำรวจ เมื่อเราเพียงแต่พยายามทำความเข้าใจข้อมูลให้ดีขึ้น

ดังนั้นหากเราเห็นว่าความโด่งเป็นบวก เรารู้ว่าเรากำลังทำงานกับการกระจายที่มีค่าข้อมูลน้อยลงใกล้กับศูนย์กลางและค่าข้อมูลมากขึ้นกระจายไปตามส่วนท้าย

ในทางกลับกัน ถ้าเราเห็นว่าความโด่งเป็นลบ เรารู้ว่าเรากำลังทำงานกับการแจกแจงที่มีค่าข้อมูลมากกว่าอยู่ใกล้ศูนย์กลางและมีค่าข้อมูลน้อยกว่าในส่วนท้าย

แหล่งข้อมูลเพิ่มเติม

หากต้องการค้นหาความเบ้และความโด่งของการแจกแจงที่กำหนด คุณสามารถป้อนค่าข้อมูลดิบลงใน เครื่องคำนวณความเบ้และความโด่ง ซึ่งจะบอกคุณทั้งความเบ้และความโด่งของการแจกแจง

หนึ่งในการทดสอบทางสถิติที่ได้รับความนิยมมากที่สุดที่ใช้ในการพิจารณาว่าการแจกแจงแบบใดแบบหนึ่งมีความเบ้และความโด่งที่สอดคล้องกับการแจกแจงแบบปกติหรือไม่คือการ ทดสอบ Jarque Bera

Khan Academy ยังมี ชุดวิดีโอดีๆ มากมาย ที่อธิบายวิธีจำแนกรูปแบบการกระจาย