วิธีการแปลง box-cox ใน r (พร้อมตัวอย่าง)

การแปลงแบบ box-cox เป็นวิธีการที่ใช้กันทั่วไปในการแปลงชุดข้อมูลที่ไม่กระจายแบบปกติให้เป็นชุด แบบกระจายแบบปกติ มากขึ้น

แนวคิดพื้นฐานเบื้องหลังวิธีนี้คือการหาค่าของ γ เพื่อให้ข้อมูลที่แปลงแล้วใกล้เคียงกับการแจกแจงแบบปกติมากที่สุด โดยใช้สูตรต่อไปนี้

• y(แลมบ์ดา) = (y ^แลม – 1) / แลม ถ้า y ≠ 0
• y(แลมบ์ดา) = log(y) ถ้า y = 0

เราสามารถทำการแปลง box-cox ใน R ได้โดยใช้ฟังก์ชัน boxcox() จากไลบรารี MASS() ตัวอย่างต่อไปนี้แสดงวิธีใช้ฟังก์ชันนี้ในทางปฏิบัติ

อ้างอิง บทความนี้ จากมหาวิทยาลัยคอนเนตทิคัตเพื่อดูบทสรุปที่ดีเกี่ยวกับการพัฒนาการเปลี่ยนแปลง Box-Cox

ตัวอย่าง: การแปลง Box-Cox ใน R

โค้ดต่อไปนี้แสดงวิธีปรับโมเดลการถดถอยเชิงเส้นให้พอดีกับชุดข้อมูล จากนั้นใช้ฟังก์ชัน boxcox() เพื่อค้นหาแลมบ์ดาที่เหมาะสมที่สุดเพื่อแปลง ตัวแปรตอบสนอง และปรับโมเดลใหม่ให้เหมาะสม

 library (MASS)

#create data
y=c(1, 1, 1, 2, 2, 2, 2, 2, 2, 3, 3, 3, 6, 7, 8)
x=c(7, 7, 8, 3, 2, 4, 4, 6, 6, 7, 5, 3, 3, 5, 8)

#fit linear regression model
model <- lm(y~x)

#find optimal lambda for Box-Cox transformation 
bc <- boxcox(y ~ x)
(lambda <- bc$x[which.max(bc$y)])

[1] -0.4242424

#fit new linear regression model using the Box-Cox transformation
new_model <- lm(((y^lambda-1)/lambda) ~ x)

แลมบ์ดาที่เหมาะสมที่สุดกลายเป็น -0.4242424 . ดังนั้น โมเดลการถดถอยใหม่จึงแทนที่ตัวแปรตอบสนองเดิม y ด้วยตัวแปร y = (y ^-0.4242424 – 1) / -0.4242424

รหัสต่อไปนี้แสดงวิธีสร้างแปลง QQ สองแปลง ใน R เพื่อให้เห็นภาพความแตกต่างในส่วนที่เหลือระหว่างแบบจำลองการถดถอยทั้งสอง:

 #define plotting area
op <- par(pty = "s", mfrow = c(1, 2))

#QQ plot for original model
qqnorm(model$residuals)
qqline(model$residuals)

#QQ plot for Box-Cox transformed model
qqnorm(new_model$residuals)
qqline(new_model$residuals)

#display both QQ plots
by(op)

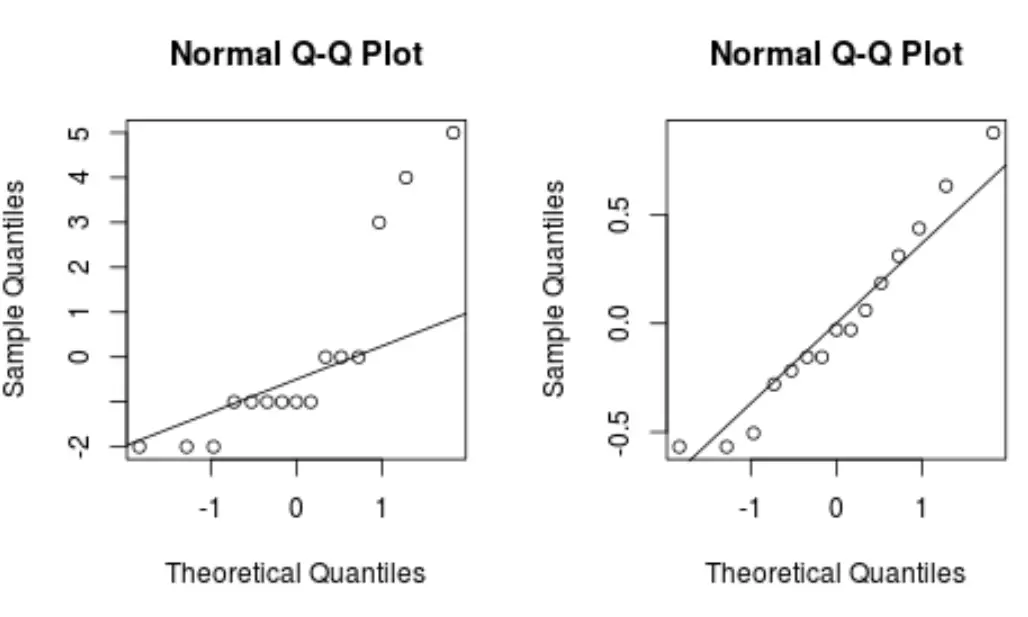
โดยทั่วไป หากจุดข้อมูลอยู่ตามแนวเส้นทแยงมุมตรงในพล็อต QQ ชุดข้อมูลน่าจะเป็นไปตามการแจกแจงแบบปกติ

สังเกตว่าแบบจำลองการแปลง box-cox สร้างพล็อต QQ ที่มีเส้นตรงกว่าแบบจำลองการถดถอยดั้งเดิมอย่างไร

สิ่งนี้บ่งชี้ว่าส่วนที่เหลือของแบบจำลองการแปลงกล่อง-ค็อกซ์นั้นมีการกระจายแบบปกติมากกว่ามาก ซึ่งเป็นไปตาม สมมติฐานข้อใดข้อหนึ่งของการถดถอยเชิงเส้น

แหล่งข้อมูลเพิ่มเติม

วิธีแปลงข้อมูลใน R (Log, Square Root, Cube Root)
วิธีสร้างและตีความพล็อต QQ ใน R
วิธีทำการทดสอบ Shapiro-Wilk เพื่อความปกติใน R