กำลังสองน้อยที่สุดบางส่วนใน python (ทีละขั้นตอน)

ปัญหาที่พบบ่อยที่สุดประการหนึ่งที่คุณจะพบในการเรียนรู้ของเครื่องคือ ความเป็นหลายส่วน สิ่งนี้เกิดขึ้นเมื่อตัวแปรทำนายตั้งแต่สองตัวขึ้นไปในชุดข้อมูลมีความสัมพันธ์กันสูง

เมื่อสิ่งนี้เกิดขึ้น แบบจำลองอาจพอดีกับชุดข้อมูลการฝึกได้ดี แต่อาจทำงานได้ไม่ดีกับชุดข้อมูลใหม่ที่ไม่เคยเห็นมาก่อน เนื่องจาก เกิน ชุดข้อมูลการฝึก ชุดฝึกซ้อม

วิธีหนึ่งในการแก้ไขปัญหานี้คือการใช้วิธีที่เรียกว่า กำลังสองน้อยที่สุดบางส่วน ซึ่งได้ผลดังนี้:

• สร้างมาตรฐานให้กับตัวแปรทำนายและการตอบสนอง
• คำนวณชุดค่าผสมเชิงเส้น M (เรียกว่า “ส่วนประกอบ PLS”) ของ ตัวแปรทำนายดั้งเดิม p ที่อธิบายการเปลี่ยนแปลงจำนวนมากในตัวแปรตอบสนองและตัวแปรทำนาย
• ใช้วิธีกำลังสองน้อยที่สุดเพื่อให้พอดีกับแบบจำลองการถดถอยเชิงเส้นโดยใช้ส่วนประกอบ PLS เป็นตัวทำนาย
• ใช้ การตรวจสอบข้าม k-fold เพื่อค้นหาจำนวนส่วนประกอบ PLS ที่เหมาะสมที่สุดเพื่อเก็บไว้ในโมเดล

บทช่วยสอนนี้ให้ตัวอย่างทีละขั้นตอนของวิธีดำเนินการกำลังสองน้อยที่สุดบางส่วนใน Python

ขั้นตอนที่ 1: นำเข้าแพ็คเกจที่จำเป็น

ขั้นแรก เราจะนำเข้าแพ็คเกจที่จำเป็นในการดำเนินการกำลังสองน้อยที่สุดบางส่วนใน Python:

 import numpy as np
import pandas as pd
import matplotlib. pyplot as plt
from sklearn. preprocessing import scale 
from sklearn import model_selection
from sklearn. model_selection import RepeatedKFold
from sklearn. model_selection import train_test_split
from sklearn. cross_decomposition import PLSRegression
from sklearn . metrics import mean_squared_error

ขั้นตอนที่ 2: โหลดข้อมูล

สำหรับตัวอย่างนี้ เราจะใช้ชุดข้อมูลชื่อ mtcars ซึ่งมีข้อมูลเกี่ยวกับรถยนต์ 33 คันที่แตกต่างกัน เราจะใช้ hp เป็นตัวแปรตอบสนอง และตัวแปรต่อไปนี้เป็นตัวทำนาย:

• mpg
• แสดง
• อึ
• น้ำหนัก
• คิววินาที

รหัสต่อไปนี้แสดงวิธีการโหลดและแสดงชุดข้อมูลนี้:

 #define URL where data is located
url = "https://raw.githubusercontent.com/Statorials/Python-Guides/main/mtcars.csv"

#read in data
data_full = pd. read_csv (url)

#select subset of data
data = data_full[["mpg", "disp", "drat", "wt", "qsec", "hp"]]

#view first six rows of data
data[0:6]


        mpg disp drat wt qsec hp
0 21.0 160.0 3.90 2.620 16.46 110
1 21.0 160.0 3.90 2.875 17.02 110
2 22.8 108.0 3.85 2.320 18.61 93
3 21.4 258.0 3.08 3.215 19.44 110
4 18.7 360.0 3.15 3.440 17.02 175
5 18.1 225.0 2.76 3.460 20.22 105

ขั้นตอนที่ 3: ปรับโมเดลกำลังสองน้อยที่สุดบางส่วนให้พอดี

รหัสต่อไปนี้แสดงวิธีปรับโมเดล PLS ให้พอดีกับข้อมูลนี้

โปรดทราบว่า cv = RepeatedKFold() บอกให้ Python ใช้ การตรวจสอบข้าม k-fold เพื่อประเมินประสิทธิภาพของโมเดล สำหรับตัวอย่างนี้ เราเลือก k = 10 เท่า ทำซ้ำ 3 ครั้ง

 #define predictor and response variables
X = data[["mpg", "disp", "drat", "wt", "qsec"]]
y = data[["hp"]]

#define cross-validation method
cv = RepeatedKFold(n_splits= 10 , n_repeats= 3 , random_state= 1 )

mse = []
n = len (X)

# Calculate MSE with only the intercept
score = -1*model_selection. cross_val_score (PLSRegression(n_components=1),
n.p. ones ((n,1)), y, cv=cv, scoring=' neg_mean_squared_error '). mean ()    
mse. append (score)

# Calculate MSE using cross-validation, adding one component at a time
for i in np. arange (1, 6):
    pls = PLSRegression(n_components=i)
    score = -1*model_selection. cross_val_score (pls, scale(X), y, cv=cv,
               scoring=' neg_mean_squared_error '). mean ()
    mse. append (score)

#plot test MSE vs. number of components
plt. plot (mse)
plt. xlabel (' Number of PLS Components ')
plt. ylabel (' MSE ')
plt. title (' hp ')

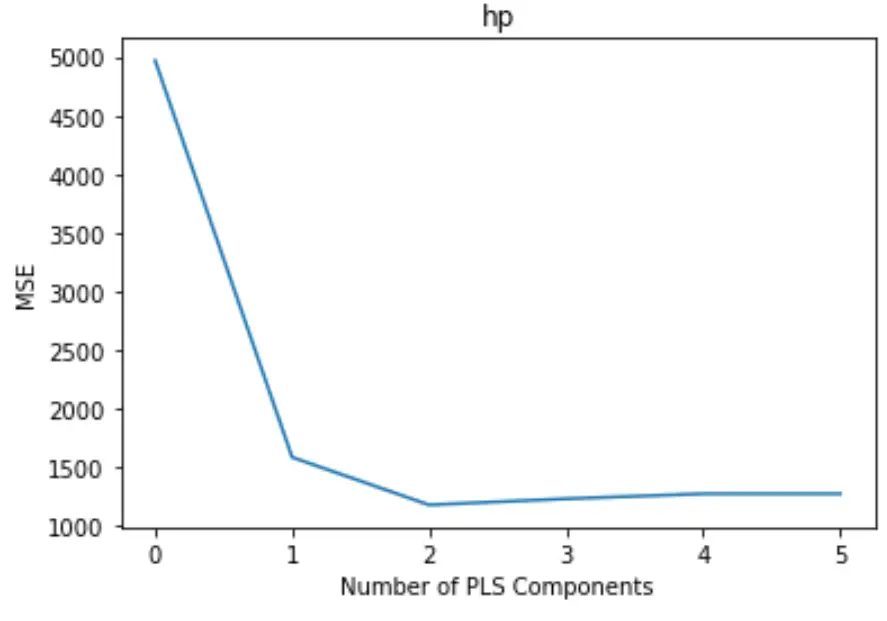
โครงเรื่องจะแสดงจำนวนส่วนประกอบ PLS ตามแกน x และการทดสอบ MSE (ค่าคลาดเคลื่อนกำลังสองเฉลี่ย) ตามแกน y

จากกราฟ เราจะเห็นว่า MSE ของการทดสอบลดลงโดยการเพิ่มองค์ประกอบ PLS สองรายการ แต่จะเริ่มเพิ่มขึ้นเมื่อเราเพิ่มองค์ประกอบ PLS มากกว่าสองรายการ

ดังนั้น โมเดลที่เหมาะสมที่สุดจึงมีเพียงส่วนประกอบ PLS สองตัวแรกเท่านั้น

ขั้นตอนที่ 4: ใช้แบบจำลองสุดท้ายเพื่อคาดการณ์

เราสามารถใช้แบบจำลอง PLS สุดท้ายกับองค์ประกอบ PLS สองส่วนเพื่อคาดการณ์เกี่ยวกับการสังเกตใหม่ๆ

รหัสต่อไปนี้แสดงวิธีแยกชุดข้อมูลต้นฉบับออกเป็นชุดการฝึกอบรมและชุดทดสอบ และใช้แบบจำลอง PLS กับส่วนประกอบ PLS สองรายการเพื่อคาดการณ์ชุดทดสอบ

 #split the dataset into training (70%) and testing (30%) sets
X_train , _

#calculate RMSE
pls = PLSRegression(n_components=2)
pls. fit (scale(X_train), y_train)

n.p. sqrt (mean_squared_error(y_test, pls. predict (scale(X_test))))

29.9094

เราจะเห็นว่า RMSE ของการทดสอบกลายเป็น 29.9094 นี่คือค่าเบี่ยงเบนเฉลี่ยระหว่างค่า HP ที่คาดการณ์ไว้กับค่า HP ที่สังเกตได้สำหรับการสังเกตชุดทดสอบ

สามารถดูโค้ด Python แบบเต็มที่ใช้ในตัวอย่างนี้ ได้ ที่นี่