ขีดจำกัดการควบคุม

โดย ดร.เบนจามิน แอนเดอร์สัน สิงหาคม 2, 2023 การจัดการคุณภาพ 0 ความคิดเห็น

บทความนี้จะอธิบายว่าขีดจำกัดการควบคุมคืออะไร และขีดจำกัดการควบคุมที่แตกต่างกันของแผนภูมิควบคุมคืออะไร นอกจากนี้ คุณยังจะได้เห็นวิธีคำนวณขีดจำกัดการควบคุม ตลอดจนตัวอย่างการทำงานซึ่งมีการกำหนดขีดจำกัดการควบคุมของกระบวนการด้วย

ขีดจำกัดการควบคุมคืออะไร?

ขีดจำกัดการควบคุม คือเส้นแนวนอนบนแผนภูมิควบคุมที่ใช้ในการพิจารณาว่ากระบวนการได้รับการควบคุมหรือไม่

แผนภูมิควบคุมมีขีดจำกัดการควบคุมสองแบบ: ขีดจำกัดการควบคุมด้านบนและด้านล่าง ซึ่งแบ่งเขตพื้นที่ควบคุมด้านบนและด้านล่างตามลำดับ

ดังนั้น ขีดจำกัดการควบคุมคือค่าที่ใช้ระบุพื้นที่ควบคุมของกระบวนการ หากการวัดที่ได้จากกระบวนการอยู่ภายในขีดจำกัดการควบคุม แสดงว่ากระบวนการได้รับการควบคุม มิฉะนั้นจะต้องตรวจสอบเครื่องจักรหรือกระบวนการเนื่องจากมีแนวโน้มว่าจะเบี่ยงเบนไป

ประเภทของขีดจำกัดการควบคุม

ขีดจำกัดการควบคุมคือ:

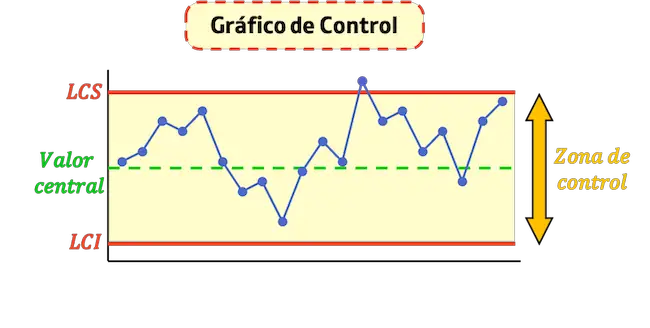
Upper Control Limit (LCS) : นี่คือบรรทัดที่ระบุค่าสูงสุดที่ยอมรับในกระบวนการ
ขีดจำกัดการควบคุมล่าง (LCI) : นี่คือเส้นที่ระบุค่าต่ำสุดที่ยอมรับในกระบวนการ
เส้นควบคุมกลาง : นี่คือเส้นที่แสดงค่าเฉลี่ยของกราฟ ยิ่งจุดอยู่ใกล้เส้นนี้มากเท่าไร กระบวนการก็จะยิ่งมีเสถียรภาพมากขึ้นเท่านั้น

วิธีการคำนวณขีดจำกัดการควบคุม

ในปัจจุบัน ขีดจำกัดการควบคุมของกระบวนการโดยทั่วไปจะคำนวณโดยซอฟต์แวร์คอมพิวเตอร์ที่ช่วยให้สามารถควบคุมกระบวนการได้ อย่างไรก็ตาม สิ่งสำคัญคือคุณต้องทราบวิธีการคำนวณ เนื่องจากคุณอาจต้องค้นหาด้วยตนเอง

การคำนวณขีดจำกัดการควบคุมของแผนภูมิควบคุมจะขึ้นอยู่กับประเภทของแผนภูมิที่คุณต้องการสร้าง เนื่องจากค่าจะเปลี่ยนไปขึ้นอยู่กับว่าเป็นแผนภูมิควบคุมสำหรับค่าเฉลี่ยหรือช่วง

แผนภูมิควบคุมค่าเฉลี่ย คือกราฟที่ใช้ประเมินวิวัฒนาการของค่าเฉลี่ยของกระบวนการ ดังนั้นค่าเฉลี่ยของชุดค่าจึงคำนวณโดยใช้สูตรต่อไปนี้:

$\overline{X}=\cfrac{\displaystyle \sum_{i=1}^n x_i}{n}$

ทอง:

$x_i$

คือเลขวัด i
$n$

คือจำนวนการวัดที่ทำ

เราจะกำหนดค่ากลางของแผนภูมิควบคุมสำหรับค่าเฉลี่ยเป็น

$\overline{\overline{X}}$

ซึ่งเป็นค่าเฉลี่ยของกลุ่มตัวอย่างและคำนวณด้วยนิพจน์ต่อไปนี้

$\overline{\overline{X}}=\cfrac{\displaystyle \sum_{j=1}^m {\overline{X}_j}}{m}$

ทอง:

$\overline{X}_j$

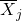
คือค่าเฉลี่ยของกลุ่มตัวอย่าง j
$m$

คือจำนวนตัวอย่างที่ถ่าย

➤ ดู: การคำนวณค่าเฉลี่ยเลขคณิต

ในทางตรงกันข้าม ค่ากลางของ แผนภูมิควบคุมขอบเขต คือค่าเฉลี่ยของขอบเขตของกลุ่มตัวอย่างทั้งหมดที่นำมา:

$\overline{R}=\cfrac{\displaystyle \sum_{j=1}^m R_j}{m}$

ทอง:

$R_j$

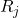
คือพิสัยของกลุ่มตัวอย่าง j
$m$

คือจำนวนตัวอย่างที่ถ่าย

➤ ดู: การคำนวณช่วงทางสถิติ

ดังนั้น สูตรในการคำนวณขีดจำกัดการควบคุม ของแผนภูมิควบคุมจึงเป็นดังนี้:

การ์ดควบคุม

$\begin{array}{c}LCS=\overline{\overline{X}}+A_2\cdot \overline{R}\\[3ex]LCI=\overline{\overline{X}}-A_2\cdot \overline{R}\end{array}$

การ์ดควบคุม R

$\begin{array}{c}LCS=D_4\cdot \overline{R}\\[3ex]LCI=D_3\cdot\overline{R}\end{array}$

โดยที่ค่าของพารามิเตอร์ A ₂ , D ₃ และ D ₄ พบในตารางต่อไปนี้:

ขนาด (หมายเลข)	เวลา ₂	วันที่ ₃	_เจ4
2	1,880	0.000	3,267
3	1,023	0.000	2,575
4	0.729	0.000	2,282
5	0.577	0.000	2,115
6	0.483	0.000	2547
7	0.419	0.076	1,924
8	0.373	0.136	1,864
9	0.337	0.184	1,816
สิบ	0.308	0.223	1,777

ตัวอย่างการคำนวณขีดจำกัดการควบคุม

บริษัทอุตสาหกรรมแห่งหนึ่งต้องการควบคุมการวัดเส้นผ่านศูนย์กลางของกระบอกสูบเพื่อดูว่ากระบวนการผลิตอยู่ภายใต้การควบคุมหรือไม่ ในการดำเนินการนี้ ให้นำตัวอย่าง 5 กระบอกสูบทุกๆ 15 นาทีแล้ววัดเส้นผ่านศูนย์กลาง ตารางต่อไปนี้แสดงการบันทึกการวัด

ในการค้นหาขีดจำกัดการควบคุม เราต้องใช้ค่าเฉลี่ยเลขคณิตและช่วงของการวัดแต่ละชุดก่อน:

ทีนี้มาคำนวณค่าเฉลี่ยของค่าเฉลี่ยและช่วงซึ่งจะเป็นค่ากลางของแผนภูมิควบคุมสำหรับค่าเฉลี่ยและช่วงตามลำดับ:

$\overline{\overline{X}}=\cfrac{\displaystyle \sum_{j=1}^m {\overline{X}_j}}{m}=4,8589$

$\overline{R}=\cfrac{\displaystyle \sum_{j=1}^m R_j}{m}=0,0227$

ในกรณีนี้ แต่ละตัวอย่างจะประกอบด้วยการวัด 5 ครั้ง ค่าสัมประสิทธิ์ของสูตรขีดจำกัดการควบคุมจึงเป็นดังนี้:

$A_2=0,577$

$D_3=0$

$D_4=2,115$

เราคำนวณขีดจำกัดการควบคุมบนและล่างของแผนภูมิควบคุมเฉลี่ยและแผนภูมิควบคุมแบบขยาย:

ขีดจำกัดการควบคุมแผนภูมิควบคุม

$\begin{array}{c}LCS=\overline{\overline{X}}+A_2\cdot \overline{R}=4,8589+0,577\cdot 0,0227=4,8720\\[3ex]LCI=\overline{\overline{X}}-A_2\cdot \overline{R}=4,8589-0,577\cdot 0,0227=4,8458\end{array}$

ขีดจำกัดการควบคุมของ การ์ดควบคุม R

$\begin{array}{c}LCS=D_4\cdot \overline{R}=2,115\cdot 0,0227=0,0481\\[3ex]LCI=D_3\cdot\overline{R}=0\cdot 0,0227=0\end{array}$

การ์ดควบคุมการฝึกจึงมีดังต่อไปนี้:

ในแผนภูมิควบคุมแรก เราจะเห็นว่าค่าสองค่านั้นน้อยกว่าขีดจำกัดการควบคุมด้านล่าง นอกจากนี้ ในแผนภูมิควบคุมที่สอง ยังมีค่าที่อยู่เหนือขีดจำกัดการควบคุมด้านบนด้วย กระบวนการนี้จึงไม่ได้รับการควบคุม

เกี่ยวกับผู้แต่ง

ดร.เบนจามิน แอนเดอร์สัน

สวัสดี ฉันชื่อเบนจามิน ศาสตราจารย์สถิติเกษียณอายุแล้ว และผันตัวมาเป็นครูสอนสถิติโดยเฉพาะ ด้วยประสบการณ์และความเชี่ยวชาญที่กว้างขวางในสาขาสถิติ ฉันกระตือรือร้นที่จะแบ่งปันความรู้ของฉันเพื่อเสริมศักยภาพนักเรียนผ่าน Statorials. รู้เพิ่มเติม

ขีดจำกัดการควบคุมคืออะไร?

ประเภทของขีดจำกัดการควบคุม

วิธีการคำนวณขีดจำกัดการควบคุม

ตัวอย่างการคำนวณขีดจำกัดการควบคุม

เกี่ยวกับผู้แต่ง

ดร.เบนจามิน แอนเดอร์สัน

เพิ่มความคิดเห็น