วิธีการคำนวณข้อผิดพลาด root mean square (rmse) ใน excel

ในสถิติ การ วิเคราะห์การถดถอย เป็นเทคนิคที่เราใช้เพื่อทำความเข้าใจความสัมพันธ์ระหว่างตัวแปรทำนาย x และตัวแปรตอบสนอง y

เมื่อเราทำการวิเคราะห์การถดถอย เราจะได้แบบจำลองที่บอกเราถึงค่าที่ทำนายของตัวแปรตอบสนองตามค่าของตัวแปรทำนาย

วิธีหนึ่งในการประเมินว่าแบบจำลองของเราเหมาะกับชุดข้อมูลที่กำหนดได้ดีเพียงใด การคำนวณค่า เฉลี่ยกำลังสองของข้อผิดพลาด ซึ่งเป็นตัวชี้วัดที่บอกเราว่าค่าที่คาดการณ์ของเรานั้นอยู่ห่างจากค่าที่สังเกตได้โดยเฉลี่ยเท่าใด

สูตรในการค้นหาค่าคลาดเคลื่อนกำลังสองเฉลี่ยหรือที่เรียกกันทั่วไปว่า RMSE คือ:

RMSE = √[ Σ(P _ผม – O _ผม ) ² / n ]

ทอง:

• Σ เป็นสัญลักษณ์แฟนซีที่หมายถึง “ผลรวม”
• P _i คือค่าที่ทำนายไว้สำหรับการสังเกต ^{ครั้งที่ 3} ในชุดข้อมูล
• O _i คือค่าที่สังเกตได้สำหรับการสังเกต ^{ครั้งที่ 3} ในชุดข้อมูล
• n คือขนาดตัวอย่าง

หมายเหตุ ทางเทคนิค :

• ค่าคลาดเคลื่อนกำลังสองเฉลี่ยสามารถคำนวณได้สำหรับแบบจำลองประเภทใดก็ได้ที่สร้างค่าที่ทำนายไว้ ซึ่งสามารถนำไปเปรียบเทียบกับค่าที่สังเกตได้ของชุดข้อมูล
• ค่าคลาดเคลื่อนกำลังสองเฉลี่ยบางครั้งเรียกว่าค่าเบี่ยงเบนกำลังสองเฉลี่ย ซึ่งมักเรียกสั้นว่า RMSD

ต่อไปเรามาดูตัวอย่างวิธีคำนวณค่าคลาดเคลื่อนกำลังสองเฉลี่ยใน Excel

วิธีการคำนวณข้อผิดพลาด Mean Square ใน Excel

ไม่มีฟังก์ชันในตัวสำหรับคำนวณ RMSE ใน Excel แต่เราสามารถคำนวณได้อย่างง่ายดายด้วยสูตรเดียว เราจะแสดงวิธีคำนวณ RMSE สำหรับสองสถานการณ์ที่แตกต่างกัน

สถานการณ์ที่ 1

ในสถานการณ์ คุณสามารถมีคอลัมน์หนึ่งที่มีค่าที่คาดการณ์จากแบบจำลองของคุณ และอีกคอลัมน์หนึ่งที่มีค่าที่สังเกตได้ รูปภาพด้านล่างแสดงตัวอย่างของสถานการณ์นี้:

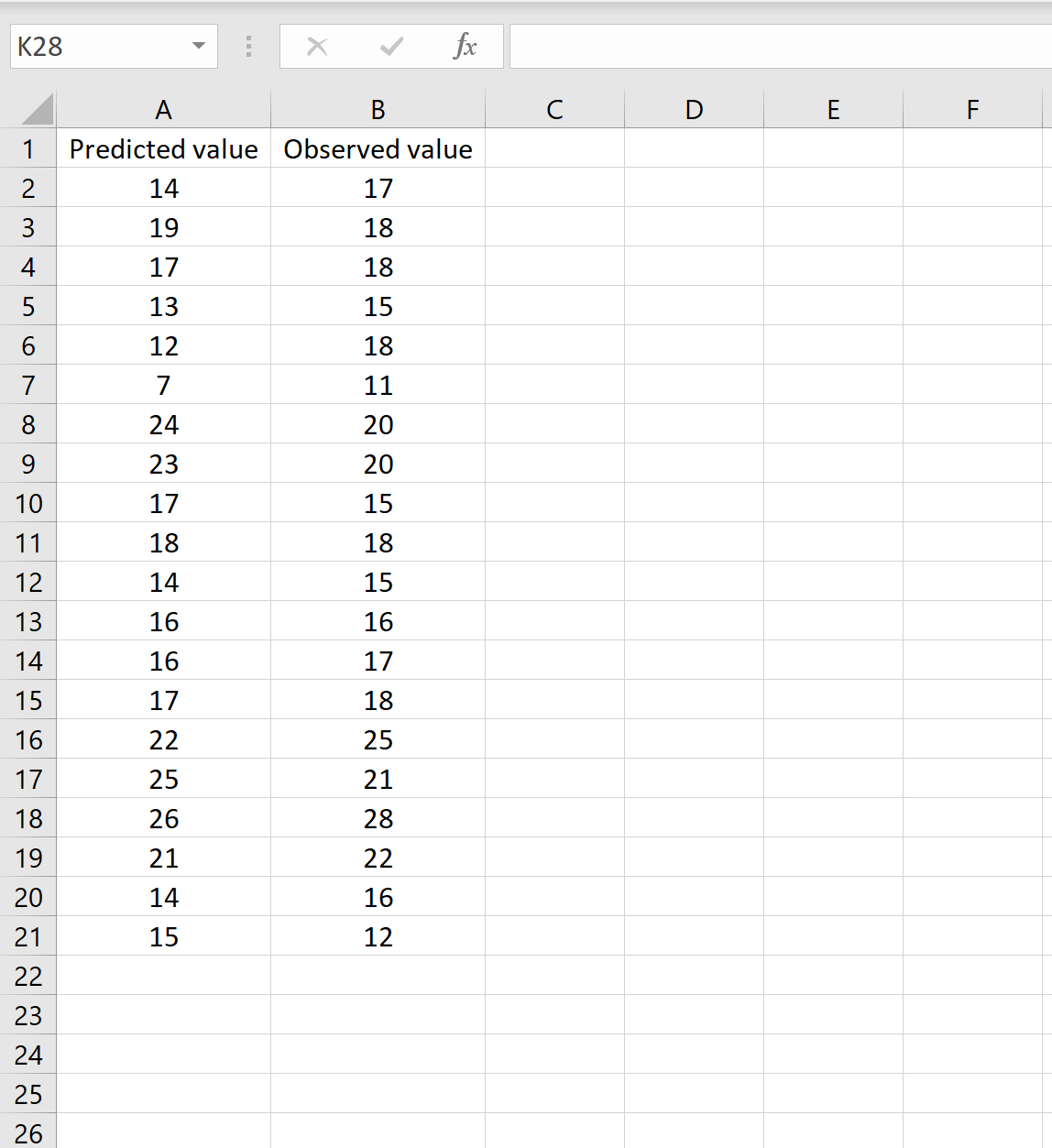
ถ้าเป็นเช่นนั้น คุณสามารถคำนวณ RMSE ได้โดยการพิมพ์สูตรต่อไปนี้ในเซลล์ใดๆ แล้วคลิก CTRL+SHIFT+ENTER:

=SQRT(SUMSQ(A2:A21-B2:B21) / COUNT(A2:A21))

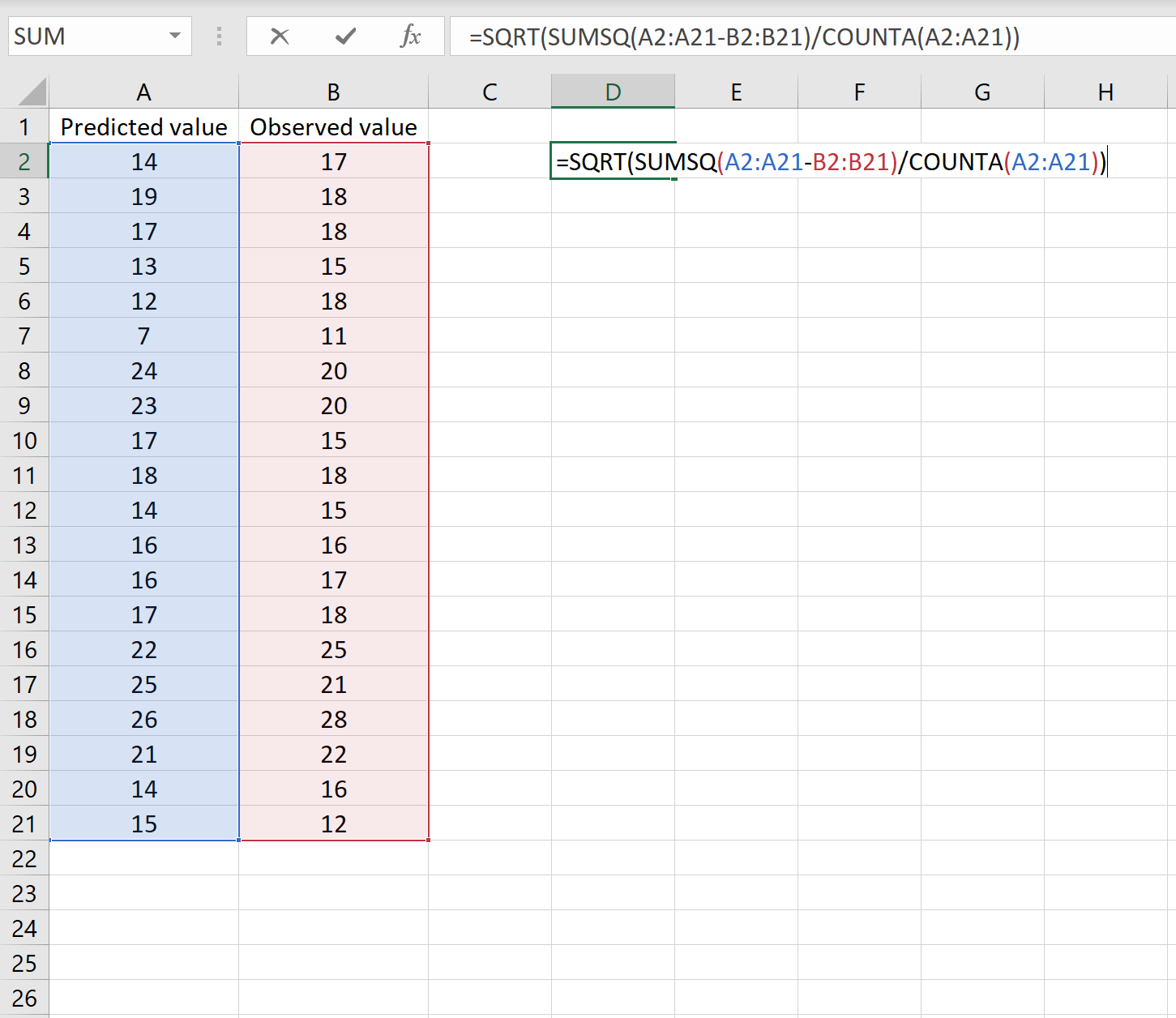
นี่บอกเราว่าค่าคลาดเคลื่อนกำลังสองเฉลี่ยคือ 2.6646

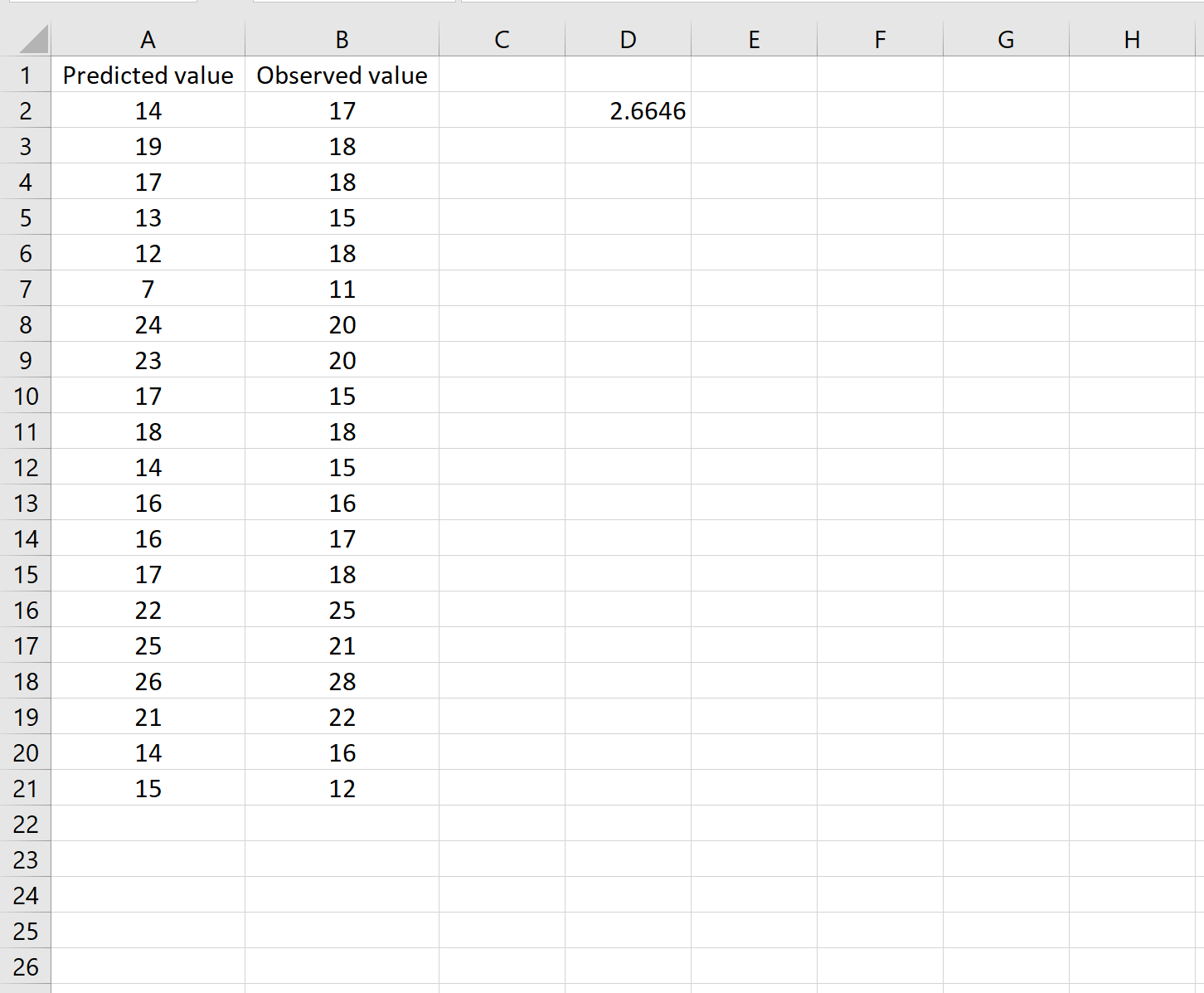
สูตรอาจดูยุ่งยากเล็กน้อย แต่ก็สมเหตุสมผลเมื่อคุณแยกย่อย:

= SQRT( SUMSQ(A2:A21-B2:B21) / COUNT(A2:A21) )

• ขั้นแรก เราคำนวณผลรวมของกำลังสองของความแตกต่างระหว่างค่าที่คาดการณ์และค่าที่สังเกตได้โดยใช้ฟังก์ชัน SUMSQ()
• ต่อไป เราจะหารด้วยขนาดตัวอย่างของชุดข้อมูลโดยใช้ COUNTA() ซึ่งจะนับจำนวนเซลล์ในช่วงที่ไม่ว่างเปล่า
• สุดท้าย เราจะหารากที่สองของการคำนวณทั้งหมดโดยใช้ฟังก์ชัน SQRT()

สถานการณ์ที่ 2

ในสถานการณ์อื่น คุณอาจคำนวณความแตกต่างระหว่างค่าที่คาดการณ์และค่าที่สังเกตได้แล้ว ในกรณีนี้ คุณจะมีเพียงคอลัมน์เดียวที่แสดงความแตกต่าง

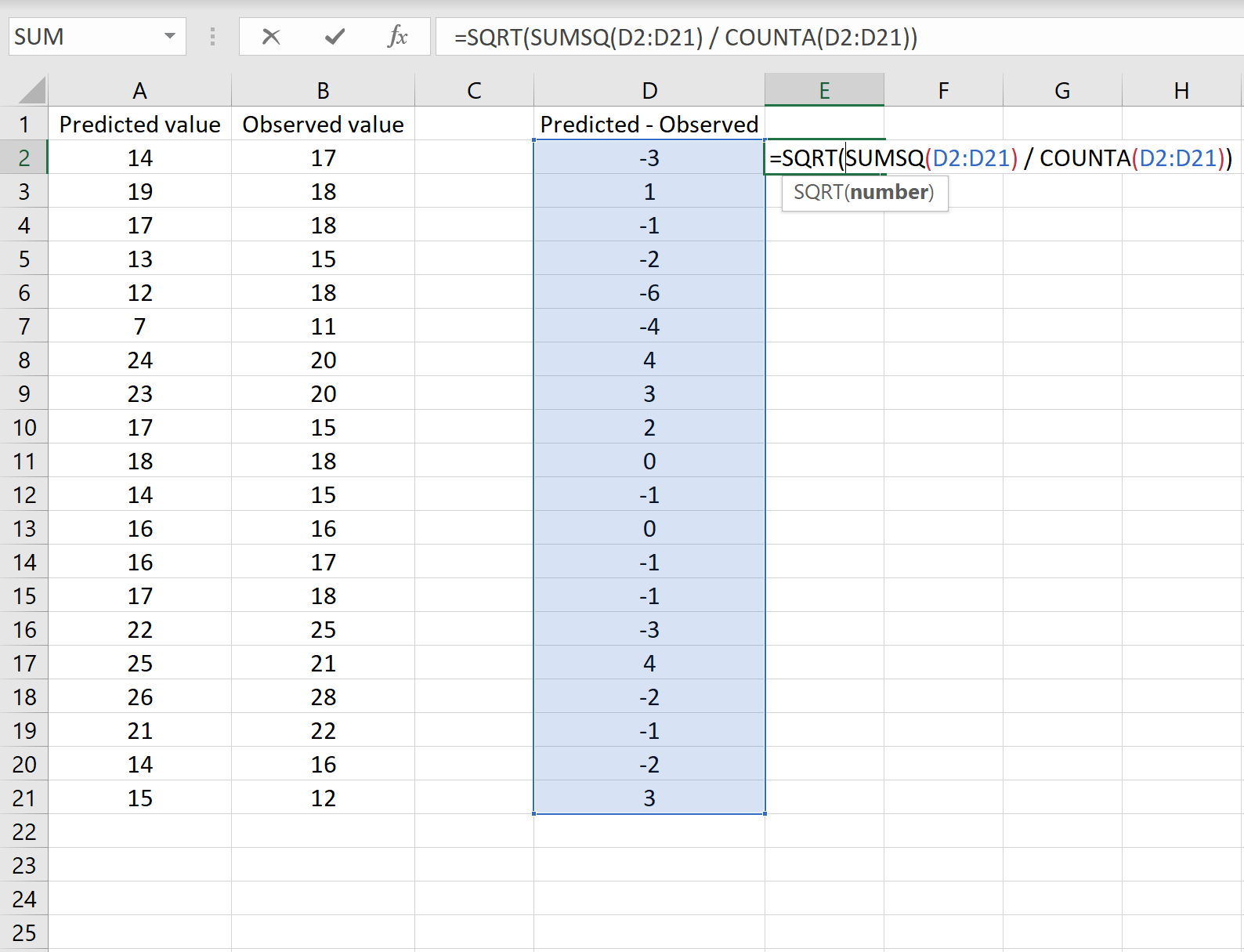
รูปภาพด้านล่างแสดงตัวอย่างของสถานการณ์นี้ ค่าที่คาดการณ์จะแสดงในคอลัมน์ A ค่าที่สังเกตได้ในคอลัมน์ B และความแตกต่างระหว่างค่าที่ทำนายและค่าที่สังเกตได้ในคอลัมน์ D:

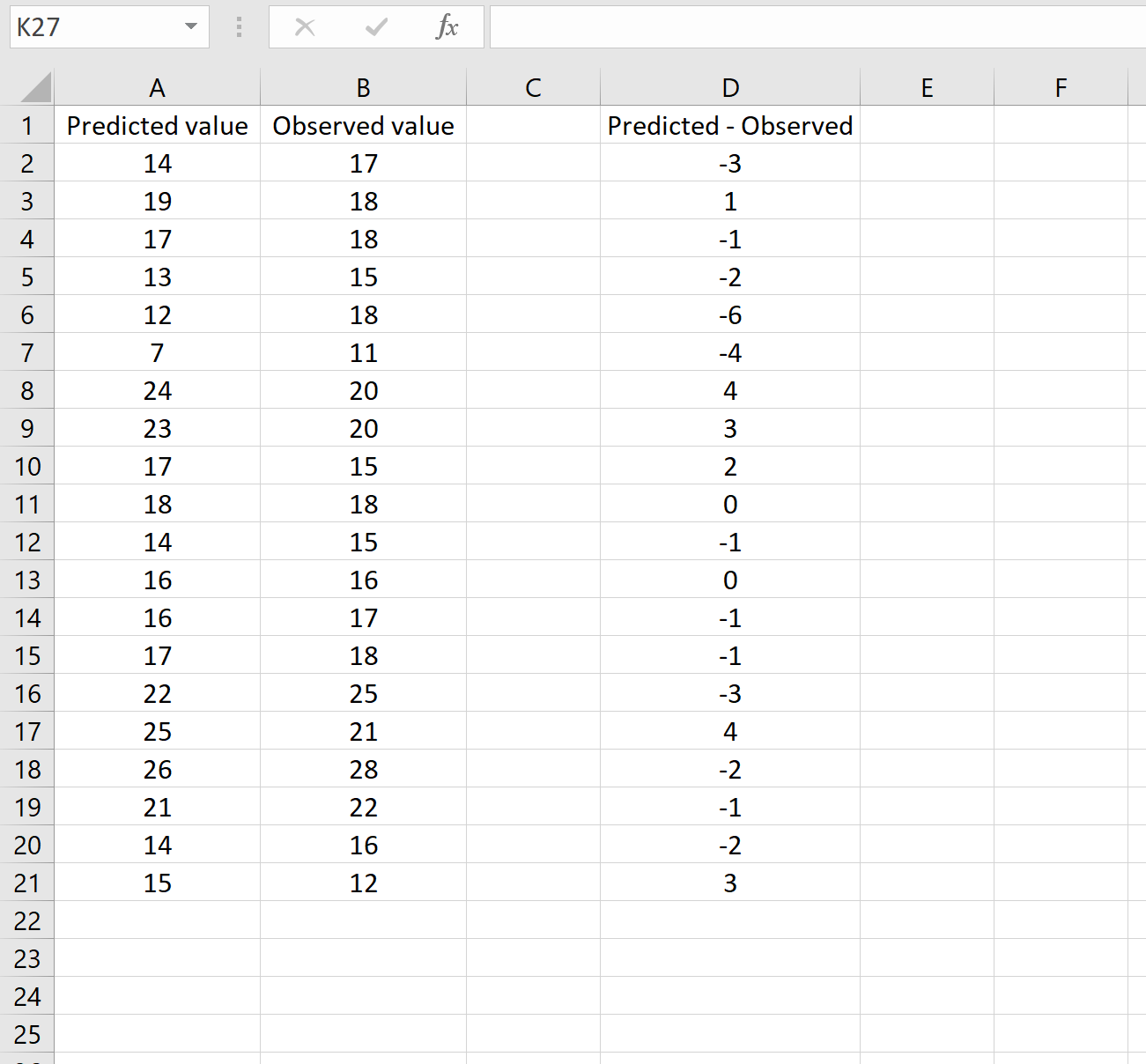
ถ้าเป็นเช่นนั้น คุณสามารถคำนวณ RMSE ได้โดยการพิมพ์สูตรต่อไปนี้ในเซลล์ใดๆ แล้วคลิก CTRL+SHIFT+ENTER:

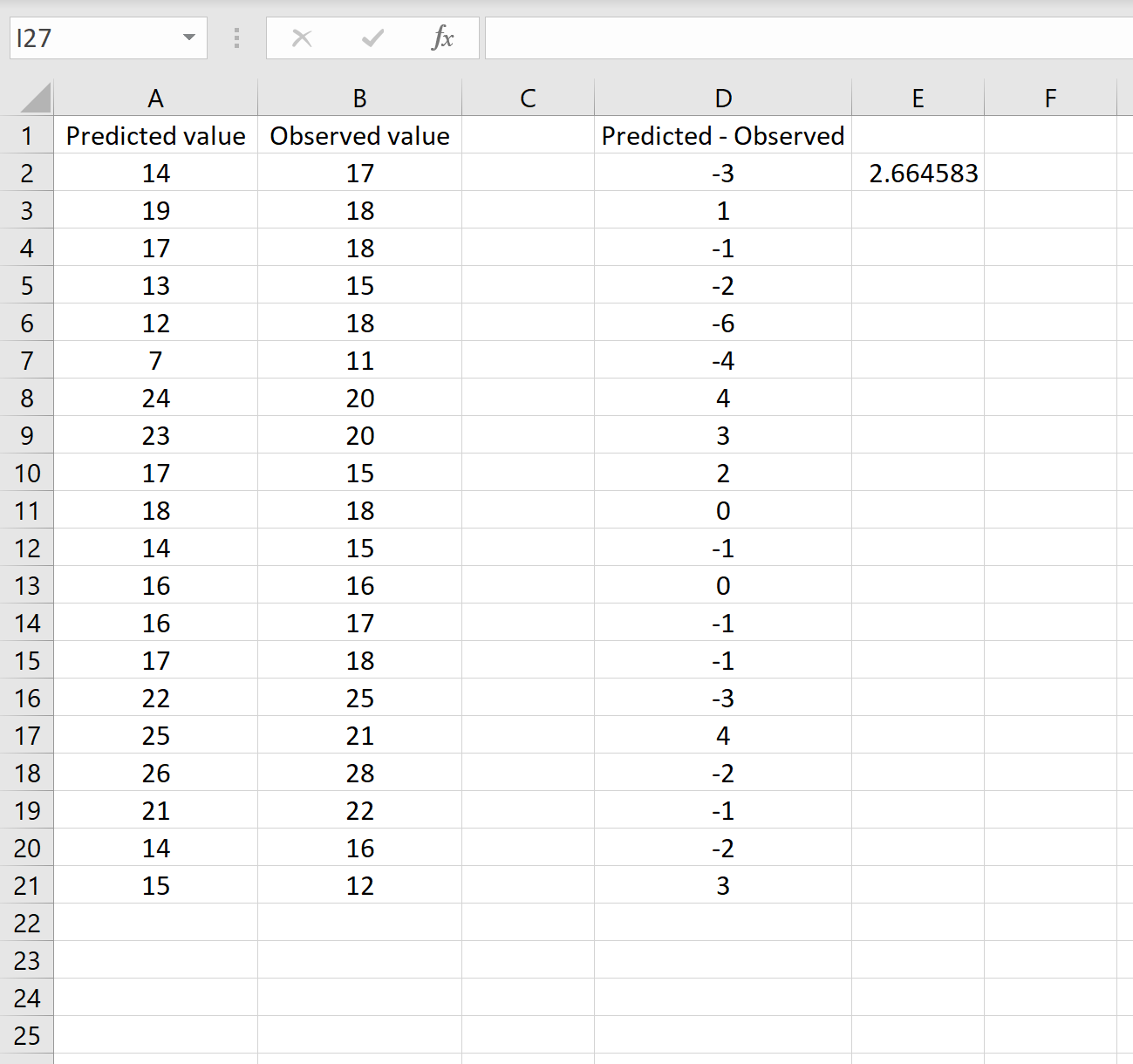
=SQRT(SUMSQ(D2:D21) / COUNT(D2:D21))

สิ่งนี้บอกเราว่าค่าคลาดเคลื่อนกำลังสองเฉลี่ยคือ 2.6646 ซึ่งสอดคล้องกับผลลัพธ์ที่ได้รับในสถานการณ์แรก นี่เป็นการยืนยันว่าทั้งสองวิธีในการคำนวณ RMSE นั้นเทียบเท่ากัน

สูตรที่เราใช้ในสถานการณ์นี้แตกต่างจากที่เราใช้ในสถานการณ์ก่อนหน้านี้เพียงเล็กน้อยเท่านั้น:

= SQRT( SUMSQ(D2:D21) / COUNT(D2:D21) )

• เนื่องจากเราได้คำนวณความแตกต่างระหว่างค่าที่คาดการณ์และค่าที่สังเกตได้ในคอลัมน์ D แล้ว เราจึงสามารถคำนวณผลรวมของความแตกต่างกำลังสองได้โดยใช้ฟังก์ชัน SUMSQ()   ฟังก์ชั่นที่มีเฉพาะค่าจากคอลัมน์ D
• ต่อไป เราจะหารด้วยขนาดตัวอย่างของชุดข้อมูลโดยใช้ COUNTA() ซึ่งจะนับจำนวนเซลล์ในช่วงที่ไม่ว่างเปล่า
• สุดท้าย เราจะหารากที่สองของการคำนวณทั้งหมดโดยใช้ ฟังก์ชัน SQRT()

วิธีการตีความ RMSE

ตามที่กล่าวไว้ข้างต้น RMSE เป็นวิธีที่มีประโยชน์ในการดูว่าแบบจำลองการถดถอย (หรือแบบจำลองใดๆ ที่สร้างค่าที่คาดการณ์) สามารถ “พอดี” ชุดข้อมูลได้ดีเพียงใด

ยิ่ง RMSE มีขนาดใหญ่เท่าใด ความแตกต่างระหว่างค่าที่คาดการณ์กับค่าที่สังเกตได้ก็จะยิ่งมากขึ้น ซึ่งหมายความว่าโมเดลการถดถอยจะเข้ากับข้อมูลได้แย่ลง ในทางกลับกัน ยิ่ง RMSE มีขนาดเล็ก โมเดลก็ยิ่งสามารถใส่ข้อมูลได้ดีขึ้นเท่านั้น

อาจมีประโยชน์อย่างยิ่งในการเปรียบเทียบ RMSE ของโมเดลสองโมเดลที่แตกต่างกันเพื่อดูว่าโมเดลใดเหมาะสมกับข้อมูลมากที่สุด

สำหรับบทช่วยสอนเพิ่มเติมใน Excel โปรดตรวจดู หน้าคำแนะนำ Excel ของเรา ซึ่งแสดงรายการบทช่วยสอน Excel ทั้งหมดเกี่ยวกับสถิติ