ความถี่สะสม

บทความนี้จะอธิบายว่าสถิติมีความถี่สะสมเท่าใด ดังนั้น คุณจะได้เรียนรู้ความหมายของความถี่สะสม วิธีคำนวณความถี่สะสมด้วยตัวอย่าง และสุดท้ายคือความถี่สะสมประเภทต่างๆ ที่มีอยู่

ความถี่สะสมคืออะไร?

ในสถิติ ความถี่สะสม คือผลรวมของความถี่สะสม นั่นคือความถี่สะสมของค่าจะเท่ากับความถี่ของค่านั้นบวกกับความถี่ของค่าที่ต่ำกว่าทั้งหมด

ความถี่สะสมมีสองประเภท: ความถี่สัมบูรณ์สะสม และความถี่สัมพัทธ์สะสม ด้านล่างนี้เราจะดูว่าความถี่สะสมแต่ละประเภทคำนวณอย่างไร

โปรดทราบว่าเพื่อที่จะเข้าใจว่าความถี่สะสมหมายถึงอะไรในสถิติ คุณต้องเข้าใจแนวคิดเรื่องความถี่ให้ชัดเจนก่อน ด้วยเหตุนี้จึงแนะนำให้ไปที่โพสต์ต่อไปนี้ก่อนที่จะดำเนินการอธิบายต่อ:

วิธีการคำนวณความถี่สะสม

ขั้นตอนใน การคำนวณความถี่สะสม ของกลุ่มตัวอย่างทางสถิติมีดังนี้:

1. สร้างตารางที่มีค่าต่างๆ ทั้งหมดที่ปรากฏในชุดข้อมูล เรียงลำดับจากน้อยไปหามาก
2. ค้นหาความถี่สัมบูรณ์ของแต่ละค่า
3. ค้นหาความถี่สะสมของแต่ละค่า ซึ่งคำนวณโดยการบวกความถี่ของค่านั้นบวกกับความถี่ของค่าที่น้อยกว่าทั้งหมด

ดังนั้นสูตรคำนวณความถี่สะสมคือ:

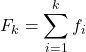
ทอง:

• 

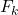
  คือความถี่สะสมของค่า

  

  .

• 

  คือความถี่สัมบูรณ์ของค่า

  

  .

โปรดทราบว่าขั้นตอนเหล่านี้ใช้สำหรับการคำนวณความถี่สัมพัทธ์สะสม แต่ก็มีความถี่สัมพัทธ์สะสมเช่นกัน ด้านล่างนี้เราจะเห็นความแตกต่างระหว่างความถี่สะสมทั้งสองประเภทนี้และวิธีการค้นพบแต่ละประเภท

ประเภทของความถี่สะสม

ในทางสถิติ ความถี่สะสมมี 2 ประเภท :

• ความถี่สัมบูรณ์สะสม : นี่คือผลรวมสะสมของ ความถี่สัมบูรณ์
• ความถี่สัมพัทธ์สะสม : นี่คือผลรวมสะสมของ ความถี่สัมพัทธ์

เมื่อพิจารณาถึงคำจำกัดความของความถี่สะสมแต่ละประเภท คุณสามารถดูตัวอย่างวิธีการได้รับความถี่แต่ละประเภทได้ด้านล่าง

ความถี่สัมบูรณ์สะสม

ความถี่สัมบูรณ์สะสม แสดงด้วยสัญลักษณ์ F _i และคำนวณโดยการเพิ่มความถี่สัมบูรณ์ของค่าเท่ากับหรือน้อยกว่าค่าที่เป็นปัญหา ต่อไป คุณมีตัวอย่างที่ชัดเจนในการคำนวณความถี่สัมบูรณ์สะสมของชุดข้อมูลทางสถิติ

• คะแนนที่ได้รับในวิชาสถิติในชั้นเรียนจำนวน 30 คน มีดังนี้ ความถี่สัมบูรณ์สะสมของแต่ละโน้ตคือเท่าใด

เนื่องจากตัวเลขทั้งหมดสามารถเป็นจำนวนเต็มได้เท่านั้น จึงเป็นตัวแปรที่ไม่ต่อเนื่อง จึงไม่จำเป็นที่จะต้องจัดกลุ่มข้อมูลเป็นระยะๆ

ดังนั้น ในการหาความถี่สัมบูรณ์สะสม อันดับแรกเราต้องค้นหาความถี่สัมบูรณ์ของแต่ละค่า ซึ่งเป็นจำนวนครั้งที่แต่ละค่าปรากฏในตัวอย่างทางสถิติ

ตอนนี้เราทราบความถี่สัมบูรณ์ของแต่ละค่าแล้ว เราก็สามารถคำนวณความถี่สัมบูรณ์สะสมของค่าเหล่านั้นได้ ในการทำเช่นนี้ เรามีสองทางเลือก: เราจะเพิ่มความถี่สัมบูรณ์ของค่าบวกกับความถี่สัมบูรณ์ทั้งหมดของค่าที่เล็กที่สุด หรือในทางกลับกัน เราจะเพิ่มความถี่สัมบูรณ์ของค่าบวกด้วยความถี่สัมบูรณ์สะสมของค่าก่อนหน้า . ค่า.

สรุปตารางความถี่สะสมสัมบูรณ์ของการออกกำลังกายมีดังนี้:

โปรดทราบว่าความถี่สัมบูรณ์สะสมของค่าสุดท้ายจะตรงกับจำนวนข้อมูลทั้งหมดเสมอ มิฉะนั้นก็หมายความว่าคุณทำผิดพลาดในการคำนวณ

ความถี่สัมพัทธ์สะสม

ความถี่สัมพัทธ์สะสม แสดงด้วยสัญลักษณ์ H _i และคำนวณโดยการบวกความถี่สัมพัทธ์ของค่าเท่ากับหรือน้อยกว่าค่าที่เป็นปัญหา ด้านล่างนี้ คุณจะเห็นแบบฝึกหัดที่แก้ไขด้วยข้อมูลเดียวกันกับปัญหาก่อนหน้าซึ่งมีการกำหนดความถี่สัมพัทธ์สะสม

• คะแนนที่ได้รับทางสถิติในชั้นเรียนจำนวน 30 คน มีดังนี้ ความถี่สัมพัทธ์สะสมของแต่ละโน้ตคือเท่าใด

ในกรณีนี้ ตัวแปรจะไม่ต่อเนื่อง เนื่องจากไม่สามารถรับค่าทศนิยมได้ ดังนั้นจึงไม่จำเป็นต้องจัดกลุ่มข้อมูลตามช่วงเวลา แต่เราคำนวณได้โดยตรง

ดังนั้นเราจึงจัดทำตารางความถี่และกำหนดความถี่สัมบูรณ์ของแต่ละค่าที่แตกต่างกัน:

ต่อไป เราจะคำนวณความถี่สัมพัทธ์ของแต่ละค่า ซึ่งกำหนดโดยการหารความถี่สัมบูรณ์ด้วยจำนวนการสังเกตทั้งหมด (30)

และเมื่อเราคำนวณความถี่สัมบูรณ์และความถี่สัมพัทธ์ของชุดข้อมูลแล้ว เราก็จะได้ความถี่สัมพัทธ์สะสม ในการทำเช่นนี้ คุณต้องเพิ่มความถี่สัมพัทธ์ของค่าที่ต้องการบวกกับความถี่สัมพัทธ์ก่อนหน้าทั้งหมด หรือความถี่สัมพัทธ์สะสมก่อนหน้าซึ่งมีจำนวนเท่ากัน:

กล่าวโดยสรุป ตารางความถี่ที่มีความถี่สัมบูรณ์ ความถี่สัมพัทธ์ และความถี่สัมพัทธ์สะสมมีดังนี้

โปรดทราบว่าค่าสุดท้ายของความถี่สัมพัทธ์สะสมควรเป็น 1 เสมอ หากคุณได้ตัวเลขอื่น แสดงว่าคำนวณผิดพลาด