ความถี่สัมบูรณ์
บทความนี้จะอธิบายความหมายของความถี่สัมบูรณ์ในสถิติ ดังนั้น คุณจะค้นพบวิธีการรับความถี่สัมบูรณ์ของชุดข้อมูล แบบฝึกหัดที่แก้ไขแล้ว 2 แบบ และความแตกต่างจากความถี่ทางสถิติประเภทอื่น
ความถี่สัมบูรณ์คืออะไร?
ในสถิติ ความถี่สัมบูรณ์ คือจำนวนครั้งที่ค่าปรากฏในชุดข้อมูล พูดง่ายๆ ก็คือ ความถี่สัมบูรณ์คือจำนวนครั้งที่ผลลัพธ์ถูกทำซ้ำ
ตัวอย่างเช่น หากคนเจ็ดคนในแบบสำรวจตอบว่าสีโปรดของพวกเขาคือสีแดง ความถี่สัมบูรณ์ของสีแดงคือ 7
ดังนั้นผลรวมของความถี่สัมบูรณ์ของค่าทั้งหมดจึงเท่ากับจำนวนข้อมูลทั้งหมดในตัวอย่างทางสถิติ
โดยทั่วไป ตัวอักษร f ที่มีตัวห้อย i ใช้แทนความถี่สัมบูรณ์ของค่า i ดังนั้นสัญลักษณ์สำหรับความถี่สัมบูรณ์คือ fi
วิธีการคำนวณความถี่สัมบูรณ์
หากต้องการรับความถี่สัมบูรณ์ของชุดข้อมูล คุณต้องทำตามขั้นตอนต่อไปนี้:
- หากตัวแปรไม่ต่อเนื่อง ให้สร้างอาร์เรย์ของค่าต่างๆ ทั้งหมดที่ปรากฏในชุดข้อมูล กล่าวคือ วางค่าที่แตกต่างกันแต่ละค่าไว้ในแถวของตาราง
- หากตัวแปรมีความต่อเนื่อง ให้จัดกลุ่มข้อมูลเป็นช่วงๆ และสร้างตารางที่มีช่วงทั้งหมด
- นับจำนวนครั้งที่ค่าปรากฏในชุดข้อมูลและบันทึกผลลัพธ์ลงในตารางความถี่
- ทำซ้ำขั้นตอนก่อนหน้าสำหรับแต่ละค่าที่แตกต่างกันในข้อมูลตัวอย่าง
ตัวอย่างความถี่สัมบูรณ์
เมื่อเราได้เห็นคำจำกัดความของความถี่สัมบูรณ์และทฤษฎีวิธีการคำนวณแล้ว เราจะมาดูตัวอย่างสองตัวอย่างเพื่อให้คุณเข้าใจว่าความถี่ดังกล่าวทำอย่างไร ในตัวอย่างแรก เราจะกำหนดความถี่สัมบูรณ์ของตัวแปรแยกและในตัวอย่างที่สองของตัวแปรต่อเนื่อง เนื่องจากขั้นตอนจะแตกต่างกันเล็กน้อยขึ้นอยู่กับกรณี
ตัวอย่างที่ 1: ตัวแปรไม่ต่อเนื่อง
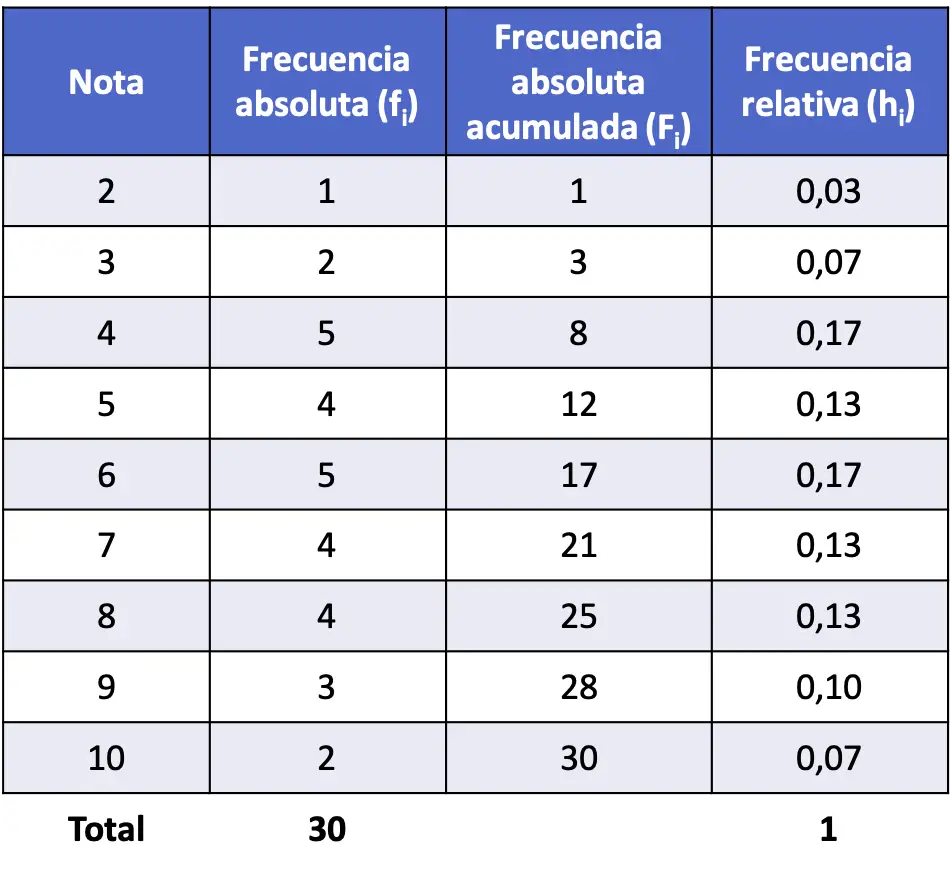
- คะแนนที่ได้รับทางสถิติในชั้นเรียนจำนวน 30 คน มีดังนี้ ความถี่สัมบูรณ์ของแต่ละโน้ตคือเท่าไร?
![]()
![]()
![]()
ในกรณีนี้ มันเป็นตัวแปรที่ไม่ต่อเนื่อง เนื่องจากมีเพียงจำนวนเต็มเท่านั้น ดังนั้นจึงไม่จำเป็นต้องจัดกลุ่มให้เป็นช่วง
ดังนั้นให้นับจำนวนครั้งที่แต่ละค่าปรากฏแล้วเขียนลงในตารางความถี่:

โปรดทราบว่าผลรวมของความถี่สัมบูรณ์ทั้งหมดเท่ากับจำนวนจุดข้อมูลทั้งหมด หากไม่ปฏิบัติตามกฎนี้ หมายความว่าคุณลืมนับข้อมูลบางอย่าง
ตัวอย่างที่ 2: ตัวแปรต่อเนื่อง
- วัดส่วนสูงจำนวน 20 คน และได้ผลลัพธ์ตามที่ระบุไว้ด้านล่างนี้ แยกข้อมูลออกเป็นระยะๆ และค้นหาความถี่สัมบูรณ์ของแต่ละช่วงเวลา
![]()
![]()
ข้อมูลในตัวอย่างนี้เป็นไปตามการแจกแจงอย่างต่อเนื่อง เนื่องจากตัวเลขอาจเป็นทศนิยมได้ ดังนั้นเราจึงจำเป็นต้องจัดกลุ่มข้อมูลเป็นช่วง ๆ ในกรณีนี้เราจะสร้างช่วงที่มีความกว้าง 10/10
ดังนั้นเราจึงนับจำนวนข้อมูลในแต่ละช่วงเวลาและแสดงความถี่สัมบูรณ์ในตาราง:

ความถี่สัมบูรณ์และความถี่สัมบูรณ์สะสม
ตามชื่อที่แสดง ความถี่สัมบูรณ์สะสมเป็นความถี่อีกประเภทหนึ่งที่ใช้ในสถิติและเกี่ยวข้องกับความถี่สัมบูรณ์
ความถี่สัมบูรณ์สะสม ของค่าจะเท่ากับผลรวมของความถี่สัมบูรณ์ของค่านั้นบวกกับความถี่สัมบูรณ์ของค่าก่อนหน้าทั้งหมด
ตามตัวอย่าง คุณสามารถดูการคำนวณความถี่สัมบูรณ์สะสมของแบบฝึกหัดแรกที่แก้ไขข้างต้นได้ที่ด้านล่าง:

ความถี่สัมบูรณ์และความถี่สัมพัทธ์
ในสถิติ ความถี่สัมพัทธ์เป็นความถี่ประเภทที่แตกต่างจากความถี่ทั้งสองที่เห็นด้านบน เนื่องจากความถี่ดังกล่าวแสดงถึงเปอร์เซ็นต์ของแต่ละค่าเมื่อเปรียบเทียบกับผลรวม นี่คือสาเหตุที่ในส่วนนี้เราจะเห็นความแตกต่างระหว่างแนวคิดทั้งสองนี้
ความแตกต่างระหว่างความถี่สัมบูรณ์และความถี่สัมพัทธ์ คือ ความถี่สัมบูรณ์คือจำนวนค่าสัมบูรณ์ในตัวอย่าง ในขณะที่ความถี่สัมพัทธ์คือสัดส่วนของแต่ละค่าต่อผลรวม
ดังนั้นความถี่สัมพัทธ์จึงคำนวณโดยการหารความถี่สัมบูรณ์ด้วยจำนวนข้อมูลทั้งหมด