วิธีการคำนวณความน่าจะเป็นปกติบนเครื่องคิดเลข ti-84

การแจกแจงแบบปกติ เป็นการแจกแจงที่ใช้บ่อยที่สุดในสถิติทั้งหมด บทช่วยสอนนี้จะอธิบายวิธีใช้ฟังก์ชันต่อไปนี้บนเครื่องคิดเลข TI-84 เพื่อค้นหาความน่าจะเป็นของการแจกแจงแบบปกติ:

Normalpdf(x, μ, σ) ส่งคืนความน่าจะเป็นที่เกี่ยวข้องกับ pdf ปกติโดยที่:

• x = ค่าส่วนบุคคล
• μ = ค่าเฉลี่ยประชากร
• σ = ส่วนเบี่ยงเบนมาตรฐานประชากร

Normalcdf(lower_x, upper_x, μ, σ) ส่งคืนความน่าจะเป็นสะสมที่เกี่ยวข้องกับ cdf ปกติระหว่างสองค่า

ทอง:

• lower_x = ค่าส่วนบุคคลที่ต่ำกว่า
• upper_x = ค่าตัวบน
• μ = ค่าเฉลี่ยประชากร
• σ = ส่วนเบี่ยงเบนมาตรฐานประชากร

ฟังก์ชันทั้งสองนี้สามารถเข้าถึงได้บนเครื่องคิดเลข TI-84 โดยกด 2 แล้วกด vars สิ่งนี้จะนำคุณไปยังหน้าจอ DISTR ซึ่งคุณสามารถใช้ Normalpdf() และ Normalcdf() :

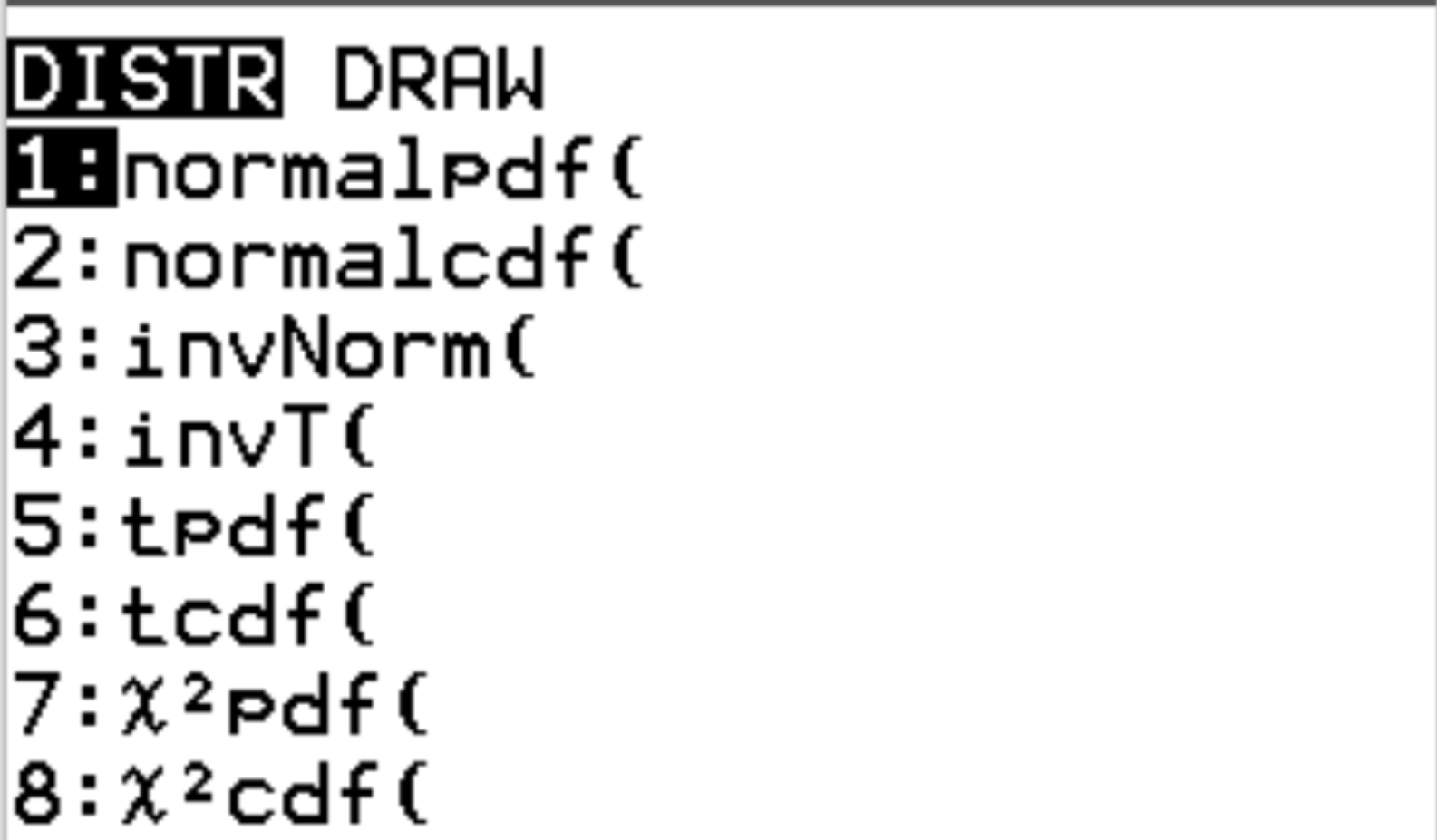
ตัวอย่างต่อไปนี้แสดงวิธีใช้ฟังก์ชันเหล่านี้เพื่อตอบคำถามต่างๆ

ตัวอย่างที่ 1: ความน่าจะเป็นปกติมากกว่า x

คำถาม: สำหรับการแจกแจงแบบปกติที่มีค่าเฉลี่ย = 40 และส่วนเบี่ยงเบนมาตรฐาน = 6 ให้ค้นหาความน่าจะเป็นที่ค่ามากกว่า 45

คำตอบ: ใช้ฟังก์ชัน Normalcdf(x, 10000, μ, σ):

ปกติcdf(45, 10,000, 40, 6) = 0.2023

หมายเหตุ: เนื่องจากฟังก์ชันต้องการค่า upper_x เราจึงใช้เพียง 10,000

ตัวอย่างที่ 2: ความน่าจะเป็นปกติน้อยกว่า x

คำถาม: สำหรับการแจกแจงแบบปกติที่มีค่าเฉลี่ย = 100 และส่วนเบี่ยงเบนมาตรฐาน = 11.3 ให้ค้นหาความน่าจะเป็นที่ค่าหนึ่งจะน้อยกว่า 98

คำตอบ: ใช้ฟังก์ชัน Normalcdf(-10000, x, μ, σ):

ปกติcdf(-10000, 98, 100, 11.3) = 0.4298

หมายเหตุ: เนื่องจากฟังก์ชันต้องการค่า lower_x เราจึงใช้เพียง -10000

ตัวอย่างที่ 3: ความน่าจะเป็นปกติระหว่างสองค่า

คำถาม: สำหรับการแจกแจงแบบปกติที่มีค่าเฉลี่ย = 50 และส่วนเบี่ยงเบนมาตรฐาน = 4 ให้ค้นหาความน่าจะเป็นที่ค่าจะอยู่ระหว่าง 48 ถึง 52

คำตอบ: ใช้ฟังก์ชัน Normalcdf(smaller_x, Larger_x, μ, σ)

ปกติcdf(48, 52, 50, 4) = 0.3829

ตัวอย่างที่ 4: ความน่าจะเป็นปกตินอกเหนือจากสองค่า

คำถาม: สำหรับการแจกแจงแบบปกติที่มีค่าเฉลี่ย = 22 และส่วนเบี่ยงเบนมาตรฐาน = 4 ให้ค้นหาความน่าจะเป็นที่ค่าน้อยกว่า 20 หรือมากกว่า 24

คำตอบ: ใช้ฟังก์ชัน Normalcdf(-10000, Small_x, μ, σ) + Normalcdf(larger_x, 10000, μ, σ)

ซีดีปกติ(-10,000, 20, 22, 4) + ซีดีปกติ(24, 10,000, 22, 4) = 0.6171