ความน่าจะเป็นเชิงทดลอง

ที่นี่คุณจะพบความหมายของความน่าจะเป็นเชิงทดลองและวิธีการคำนวณความน่าจะเป็นเชิงทดลอง นอกจากนี้ คุณจะสามารถดูตัวอย่างการคำนวณความน่าจะเป็นเชิงทดลองที่ได้รับการแก้ไขทีละขั้นตอน

ความน่าจะเป็นเชิงทดลองคืออะไร?

ความน่าจะเป็นในการทดลอง คือการวัดทางสถิติโดยอิงจากผลลัพธ์ของการทดลองหรือข้อเท็จจริงเชิงประจักษ์ และบ่งชี้ความน่าจะเป็นที่เหตุการณ์จะเกิดขึ้น

นอกจากนี้ ยิ่งทำการทดลองซ้ำมากเท่าใด ความน่าจะเป็นของการทดลองที่ได้รับก็จะยิ่งแม่นยำมากขึ้นเท่านั้น ด้วยเหตุนี้ โดยทั่วไปโปรแกรมคอมพิวเตอร์ที่สามารถจำลองการทดลองหลายพันรายการได้อย่างรวดเร็วจึงถูกนำมาใช้เพื่อกำหนดความน่าจะเป็นในการทดลอง ดังนั้นจึงได้ความแม่นยำที่ดีขึ้น

ความน่าจะเป็นเชิงทดลองเรียกอีกอย่างว่า ความน่าจะเป็นเชิงประจักษ์ หรือ ความน่าจะเป็นด้านความถี่

ความน่าจะเป็นเชิงทดลองคือตัวเลขระหว่าง 0 ถึง 1 ตามหลักตรรกะ ยิ่งค่าความน่าจะเป็นเชิงทดลองของเหตุการณ์มีมากขึ้น โอกาสที่จะเกิดขึ้นก็จะยิ่งมากขึ้น และในทางกลับกัน ยิ่งค่าน้อยลง โอกาสที่จะเกิดขึ้นก็จะน้อยลง มีแนวโน้มที่จะเกิดขึ้น หรือเหตุการณ์เกิดขึ้น แต่ค่าความน่าจะเป็นเชิงทดลองจะอยู่ระหว่างศูนย์ถึงหนึ่งเสมอ

สูตรความน่าจะเป็นเชิงทดลอง

สูตรความน่าจะเป็นในการทดลอง คือจำนวนครั้งที่เหตุการณ์เกิดขึ้นระหว่างการทดสอบหารด้วยจำนวนครั้งทั้งหมดที่ทำการทดสอบ

ตัวอย่างเช่น หากบุคคลหนึ่งขว้างลูกดอก 10 ดอกไปที่เป้าหมายและยิงได้ 6 ดอกที่ตรงกลาง ความน่าจะเป็นที่บุคคลนั้นจะยิงลูกดอกตรงกลางจะถูกคำนวณดังนี้:

ตัวอย่างความน่าจะเป็นเชิงทดลอง

เมื่อเราเห็นคำจำกัดความทางคณิตศาสตร์ของความน่าจะเป็นเชิงทดลองแล้ว เราจะแก้แบบฝึกหัดทีละขั้นตอนเกี่ยวกับความน่าจะเป็นประเภทนี้ เป้าหมายคือให้คุณเรียนรู้วิธีคำนวณความน่าจะเป็นเชิงทดลองของเหตุการณ์ ดังนั้นหากคุณมีคำถามใดๆ คุณสามารถเขียนคำถามเหล่านั้นไว้ในความคิดเห็นได้

• คำนวณความน่าจะเป็นเชิงทดลองของเหตุการณ์เบื้องต้นที่ประกอบเป็นการทดลองสุ่มในการทอยลูกเต๋า

ก่อนที่จะหาความน่าจะเป็นของการทดลอง เราจะคำนวณความน่าจะเป็นทางทฤษฎีเพื่อเปรียบเทียบผลการทดลองที่ได้กับผลทางทฤษฎี ดังที่คุณทราบดี มีผลลัพธ์ที่เป็นไปได้หกประการเมื่อทอยลูกเต๋า (1, 2, 3, 4, 5 และ 6) ดังนั้นความน่าจะเป็นทางทฤษฎีของแต่ละเหตุการณ์เบื้องต้นคือ:

เพื่อแก้ปัญหาแบบฝึกหัดนี้ เราต้องจำลองการทอยลูกเต๋าหลายครั้งและบันทึกผลลัพธ์ลงในตารางฉุกเฉิน ในกรณีนี้ เราจะทำการจำลองด้วยโปรแกรม Excel แต่คุณสามารถใช้โปรแกรมที่คุณเลือกได้อย่างชัดเจน

ก่อนอื่นเราจะจำลองการโยนสิบครั้ง จากนั้นจึงโยนหนึ่งร้อยครั้ง และสุดท้ายโยนหนึ่งพันครั้ง ด้วยวิธีนี้ เราจะสามารถวิเคราะห์ผลลัพธ์และดูว่าผลลัพธ์เปลี่ยนแปลงไปอย่างไร ขึ้นอยู่กับขนาดตัวอย่างของการทดสอบ ผลลัพธ์ที่ได้หลังจากการสุ่มจำลองการทอยลูกเต๋า 10 ครั้งมีดังนี้:

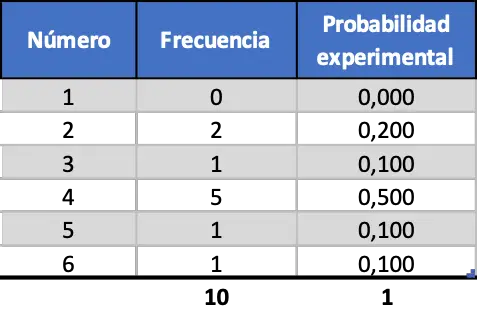
อย่างที่คุณเห็น ความน่าจะเป็นเชิงทดลองที่ได้รับในปัจจุบันค่อนข้างแตกต่างจากความน่าจะเป็นทางทฤษฎีที่คำนวณไว้ก่อนหน้านี้ (0.167)

แต่เมื่อเราเพิ่มจำนวนการทดสอบ ตัวชี้วัดทั้งสองนี้ก็มีความคล้ายคลึงกันมากขึ้น ลองดูการจำลองการเปิดตัว 100 ครั้ง:

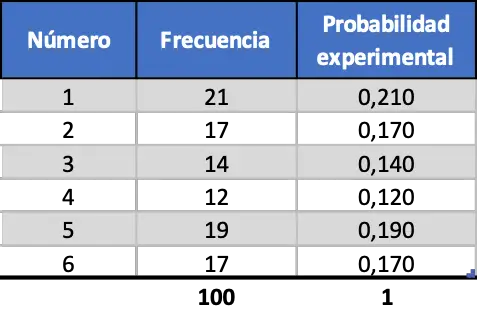
ตอนนี้ความน่าจะเป็นเชิงทดลองดูเหมือนค่าความน่าจะเป็นทางทฤษฎีมากกว่า แต่เรายังคงได้ค่าที่ห่างไกล

สุดท้าย เราทำขั้นตอนเดียวกันแต่จำลองการเปิดตัว 1,000 ครั้ง:

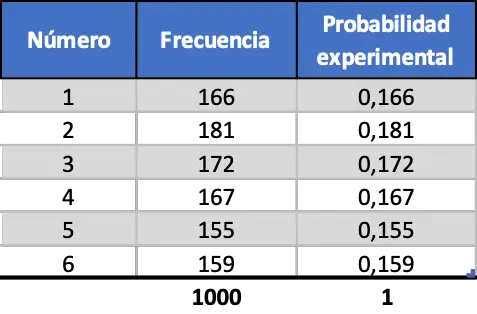
ดังที่คุณเห็นในตารางฉุกเฉินล่าสุด ตอนนี้ค่าของความน่าจะเป็นเชิงทดลองมีความคล้ายคลึงกับความน่าจะเป็นทางทฤษฎีมาก

โดยสรุป ยิ่งจำนวนการทดลองดำเนินการมากเท่าใด ค่าของความน่าจะเป็นในการทดลองของเหตุการณ์ก็จะยิ่งใกล้เคียงกับความน่าจะเป็นทางทฤษฎีมากขึ้นเท่านั้น กฎนี้ถูกกำหนดให้เป็น กฎของจำนวนมาก ซึ่งระบุว่ายิ่งมีข้อมูลมากเท่าใดค่าการทดลองก็จะยิ่งใกล้เคียงกับค่าทางทฤษฎีมากขึ้นเท่านั้น

ในทำนองเดียวกัน หากคุณเปรียบเทียบตารางความถี่ทั้งสามตาราง คุณจะเห็นว่าความน่าจะเป็นของการทดลองนั้นยังไม่เป็นที่สิ้นสุด แต่จะพัฒนาไปขึ้นอยู่กับจำนวนการทดลองที่ดำเนินการ ซึ่งหมายความว่าคุณต้องรู้วิธีตีความค่าที่ได้รับ

ความน่าจะเป็นเชิงทดลองและความน่าจะเป็นทางทฤษฎี

ความแตกต่างระหว่างความน่าจะเป็นเชิงทดลองและความน่าจะเป็นทางทฤษฎี (หรือความน่าจะเป็นแบบดั้งเดิม) ก็คือความน่าจะเป็นเชิงทดลองคำนวณจากข้อมูลที่รวบรวมจากการทดลองจริง ในขณะที่ความน่าจะเป็นทางทฤษฎีนั้นคำนวณโดยไม่จำเป็นต้องทำการทดลองใดๆ

ดังที่เราได้เห็นแล้ว เราต้องจำลองการทดลองจำนวนมากเพื่ออนุมานความน่าจะเป็นในการทดลองของเหตุการณ์หนึ่งๆ อย่างไรก็ตาม การคำนวณความน่าจะเป็นทางทฤษฎีเกี่ยวข้องกับทฤษฎีและตรรกะ คุณสามารถดูวิธีการได้ที่นี่: