ความน่าจะเป็นเชิงประจักษ์

ในบทความนี้ เราจะอธิบายวิธีคำนวณความน่าจะเป็นเชิงประจักษ์ คุณจะค้นพบว่าความน่าจะเป็นเชิงประจักษ์คืออะไร สูตรของมันคืออะไร ตัวอย่าง และอะไรคือความแตกต่างระหว่างความน่าจะเป็นเชิงประจักษ์และความน่าจะเป็นทางทฤษฎี

ความน่าจะเป็นเชิงประจักษ์คืออะไร?

ความน่าจะเป็นเชิงประจักษ์ คือการวัดทางสถิติที่อิงจากการทดลองเชิงประจักษ์หรือข้อเท็จจริงที่บ่งชี้ความน่าจะเป็นของเหตุการณ์ที่เกิดขึ้น

กล่าวอีกนัยหนึ่ง ความน่าจะเป็นเชิงประจักษ์คำนวณจากผลลัพธ์ของการทดลอง และบอกเราว่าเหตุการณ์มีแนวโน้มที่จะเกิดขึ้นมากน้อยเพียงใด

ยิ่งทำการทดลองซ้ำมากเท่าใด ความน่าจะเป็นเชิงประจักษ์ที่ได้รับก็จะยิ่งแม่นยำมากขึ้นเท่านั้น นี่คือสาเหตุที่ความน่าจะเป็นประเภทนี้มักจะถูกกำหนดโดยใช้โปรแกรมคอมพิวเตอร์ที่จำลองการวนซ้ำหลายพันรายการและสามารถวิเคราะห์ได้ในเวลาอันสั้น

ความน่าจะเป็นเชิงประจักษ์คือตัวเลขระหว่าง 0 ถึง 1 ยิ่งมีแนวโน้มว่าเหตุการณ์จะเกิดขึ้น ความน่าจะเป็นเชิงประจักษ์ก็จะยิ่งสูงขึ้น และในทางกลับกัน ยิ่งมีโอกาสที่เหตุการณ์จะเกิดขึ้นน้อยลง ความน่าจะเป็นเชิงประจักษ์ก็จะยิ่งลดลง

สูตรความน่าจะเป็นเชิงประจักษ์

สูตรสำหรับความน่าจะเป็นเชิงประจักษ์ คือจำนวนครั้งที่เหตุการณ์เกิดขึ้นระหว่างการทดลอง หารด้วยจำนวนครั้งทั้งหมดที่ทำการทดลอง

ตัวอย่างเช่น ถ้าเราดูต้นไม้สิบครั้งที่แตกต่างกันและเราได้เห็นนกบนต้นไม้เจ็ดครั้ง ความน่าจะเป็นเชิงประจักษ์ที่จะเห็นนกในขณะที่ดูต้นไม้จะเป็น:

ตัวอย่างความน่าจะเป็นเชิงประจักษ์

เมื่อพิจารณาถึงคำจำกัดความของความน่าจะเป็นเชิงประจักษ์ เราจะแก้แบบฝึกหัดความน่าจะเป็นประเภทนี้ทีละขั้นตอน วิธีนี้จะทำให้คุณสามารถดูวิธีคำนวณความน่าจะเป็นเชิงประจักษ์ได้

• คำนวณความน่าจะเป็นเชิงประจักษ์ของเหตุการณ์เบื้องต้นที่ประกอบขึ้นเป็นการทดลองสุ่มของการทอยลูกเต๋า

ขั้นแรก เราจะคำนวณความน่าจะเป็นทางทฤษฎีในการเปรียบเทียบผลการทดลองที่ได้รับกับผลทางทฤษฎี มีผลลัพธ์ที่เป็นไปได้หกประการเมื่อทอยลูกเต๋า (1, 2, 3, 4, 5 และ 6) ดังนั้นความน่าจะเป็นทางทฤษฎีของแต่ละเหตุการณ์เบื้องต้นคือ:

เพื่อแก้ปัญหาแบบฝึกหัดนี้ เราต้องจำลองการทอยลูกเต๋าหลายครั้งและบันทึกผลลัพธ์ลงในตารางฉุกเฉิน สำหรับสิ่งนี้ เราสามารถใช้ เช่น โปรแกรม Excel

เพื่อให้คุณเห็นความสำคัญของจำนวนการทดลองที่ดำเนินการ ขั้นแรกเราจะจำลองการเปิดตัวสิบครั้ง จากนั้นจึงจำลองเป็นร้อยและสุดท้ายก็พันครั้ง ดังนั้นผลลัพธ์ที่ได้จากการจำลองการสุ่มโยนลูกเต๋า 10 ครั้งแรกมีดังนี้

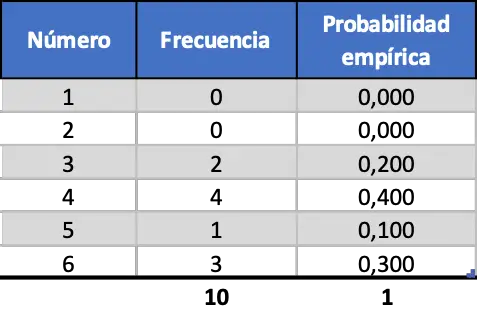
อย่างที่คุณเห็น ความน่าจะเป็นเชิงประจักษ์ที่ได้จากการจำลองการพ่นเพียง 10 ครั้งไม่ใกล้เคียงกับความน่าจะเป็นทางทฤษฎี (0.167)

แต่เมื่อเราเพิ่มจำนวนการทดสอบ เมตริกทั้งสองนี้จะคล้ายกันมากขึ้น ดูที่การจำลองการเปิดตัว 100 ครั้ง:

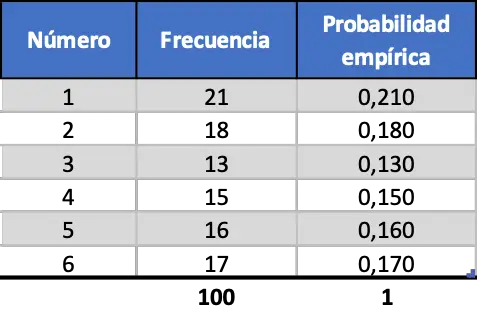
ตอนนี้ความน่าจะเป็นเชิงประจักษ์ที่คำนวณสำหรับแต่ละตัวเลขบนแม่พิมพ์นั้นมีความคล้ายคลึงกับความน่าจะเป็นทางทฤษฎีมากกว่า อย่างไรก็ตาม เรายังคงได้ค่าที่แตกต่างกันมาก

สุดท้าย เราทำขั้นตอนเดียวกันแต่จำลองการเปิดตัว 1,000 ครั้ง:

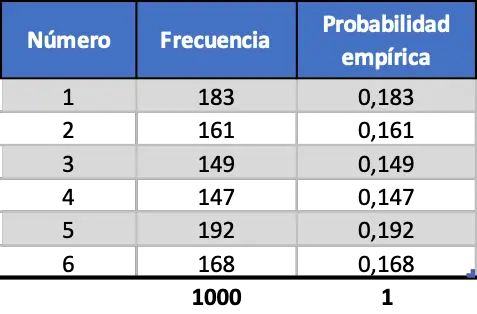
ดังที่เราเห็นในตารางฉุกเฉินล่าสุด ค่าของความน่าจะเป็นเชิงประจักษ์นั้นใกล้เคียงกับความน่าจะเป็นทางทฤษฎีมาก

โดยสรุป ยิ่งเราเพิ่มจำนวนการทดลองที่ดำเนินการมากเท่าใด ค่าของความน่าจะเป็นเชิงประจักษ์ของเหตุการณ์ก็จะยิ่งใกล้เคียงกับความน่าจะเป็นทางทฤษฎีที่จะเกิดขึ้น กฎนี้ถูกกำหนดให้เป็น กฎของจำนวนมาก ซึ่งระบุว่ายิ่งมีข้อมูลมากเท่าใดค่าการทดลองก็จะยิ่งใกล้เคียงกับค่าทางทฤษฎีมากขึ้นเท่านั้น

นอกจากนี้ หากเราเปรียบเทียบตารางความถี่ทั้งสามตาราง เราจะเห็นว่าความน่าจะเป็นเชิงประจักษ์นั้นยังไม่เป็นที่สิ้นสุด แต่จะเปลี่ยนแปลงไปขึ้นอยู่กับจำนวนการทดลองที่ดำเนินการ ซึ่งหมายความว่าคุณต้องรู้วิธีตีความค่าที่ได้รับ

ความน่าจะเป็นเชิงประจักษ์และความน่าจะเป็นทางทฤษฎี

ในที่สุด เราจะวิเคราะห์แนวคิดของความน่าจะเป็นเชิงประจักษ์และความน่าจะเป็นทางทฤษฎี เพราะถึงแม้จะเป็นความน่าจะเป็นสองประเภท แต่ก็มีความหมายที่แตกต่างไปจากเดิมอย่างสิ้นเชิง

ความแตกต่างระหว่างความน่าจะเป็นเชิงประจักษ์และความน่าจะเป็นทางทฤษฎี (หรือความน่าจะเป็นแบบคลาสสิก) คือความน่าจะเป็นเชิงประจักษ์คำนวณจากข้อมูลที่รวบรวมจากประสบการณ์จริง ในขณะที่ความน่าจะเป็นทางทฤษฎีจะคำนวณโดยคำนึงถึงสถานการณ์ในอุดมคติโดยไม่ต้องทำการทดลองใดๆ

กล่าวคือ เพื่อหาความน่าจะเป็นเชิงประจักษ์ ต้องมีการจำลองการทดลองและคำนวณตามผลลัพธ์ที่ได้รับ แต่หากต้องการทราบความน่าจะเป็นทางทฤษฎี ไม่ต้องทำการทดลองใด ๆ แต่เป็นการคำนวณทางทฤษฎี

นอกจากนี้ ระดับของอคติ ยังถูกกำหนดให้เป็นความแตกต่างระหว่างความน่าจะเป็นเชิงประจักษ์และความน่าจะเป็นทางทฤษฎี อคติอาจเป็นเชิงบวกหรือเชิงลบ แต่เป็นเรื่องยากมากที่จะให้เป็นศูนย์ เพราะนั่นหมายความว่าการทดลองแบบสุ่มจะกระทบต่อความน่าจะเป็นทางทฤษฎี ซึ่งไม่น่าเป็นไปได้อย่างยิ่ง