ความน่าจะเป็นแบบมีเงื่อนไข (หรือความน่าจะเป็นแบบมีเงื่อนไข)
ที่นี่คุณจะพบว่าความน่าจะเป็นแบบมีเงื่อนไข (หรือความน่าจะเป็นแบบมีเงื่อนไข) คืออะไร เราอธิบายวิธีการคำนวณความน่าจะเป็นแบบมีเงื่อนไขด้วยตัวอย่างและคุณสมบัติของความน่าจะเป็นประเภทนี้ นอกจากนี้ คุณจะสามารถฝึกฝนด้วยแบบฝึกหัดความน่าจะเป็นแบบมีเงื่อนไขที่มีการแก้ไขทีละขั้นตอน
ความน่าจะเป็นแบบมีเงื่อนไขคืออะไร?
ความน่าจะเป็นแบบมี เงื่อนไข หรือที่เรียกว่าความน่าจะ เป็นแบบมีเงื่อนไข คือการวัดทางสถิติที่บ่งชี้ความน่าจะเป็นที่เหตุการณ์ A จะเกิดขึ้นหากมีเหตุการณ์ B เกิดขึ้นอีก นั่นคือ ความน่าจะเป็นแบบมีเงื่อนไข P(A|B) หมายถึงความน่าจะเป็นของเหตุการณ์ A ที่เกิดขึ้นหลังจากเหตุการณ์ B เกิดขึ้นแล้ว
ความน่าจะเป็นแบบมีเงื่อนไขเขียนด้วยแถบแนวตั้งระหว่างสองเหตุการณ์: P(A|B) และอ่านได้ว่า “ความน่าจะเป็นแบบมีเงื่อนไขของเหตุการณ์ A ที่กำหนดเหตุการณ์ B”
โปรดทราบว่าค่าความน่าจะเป็นแบบมีเงื่อนไขคือตัวเลขระหว่าง 0 ถึง 1 ยิ่งความน่าจะเป็นแบบมีเงื่อนไขสูงเท่าใด โอกาสที่เหตุการณ์ A จะจะเกิดขึ้นเมื่อมีเหตุการณ์ B เกิดขึ้นก็จะยิ่งมากขึ้นเท่านั้น แต่ยิ่งความน่าจะเป็นแบบมีเงื่อนไขยิ่งต่ำ โอกาสที่เหตุการณ์ A ก็จะยิ่งน้อยลงเท่านั้น จะเกิดขึ้นเมื่อเหตุการณ์ B เกิดขึ้น
สูตรความน่าจะเป็นแบบมีเงื่อนไข
ความน่าจะเป็นแบบมีเงื่อนไขของเหตุการณ์ A ที่กำหนดโดยเหตุการณ์ B เท่ากับความน่าจะเป็นของจุดตัดระหว่างเหตุการณ์ A และเหตุการณ์ B หารด้วยความน่าจะเป็นของเหตุการณ์ B
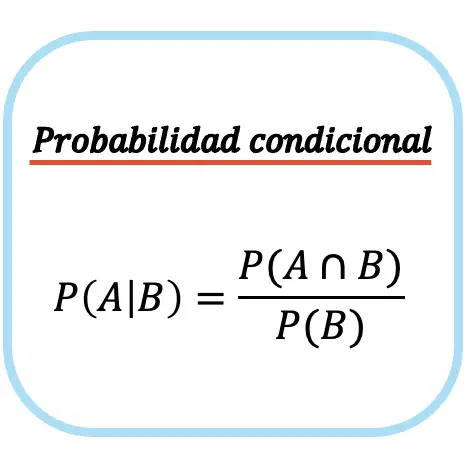
โปรดทราบว่าสูตรความน่าจะเป็นแบบมีเงื่อนไข (หรือความน่าจะเป็นแบบมีเงื่อนไข) สามารถใช้ได้ก็ต่อเมื่อความน่าจะเป็นที่เหตุการณ์ที่ไม่มีเงื่อนไขเกิดขึ้นนั้นไม่เป็นศูนย์ เช่น P(B)≠0 หรืออีกนัยหนึ่งคือหากเป็นไปได้ที่เหตุการณ์ B จะเกิดขึ้น
ความน่าจะเป็นแบบมีเงื่อนไขสามารถคำนวณได้จากค่าผกผัน กล่าวคือ ถ้าทราบ P(B|A) ก็จะสามารถคำนวณ P(A|B) ได้ แต่หากต้องการทำเช่นนี้ คุณต้องใช้ทฤษฎีบทของเบย์ คุณจะเห็นว่าทฤษฎีบทนี้ประกอบด้วยอะไรบ้าง:
ตัวอย่างความน่าจะเป็นแบบมีเงื่อนไข
เมื่อเราได้เห็นคำจำกัดความและสูตรของความน่าจะเป็นแบบมีเงื่อนไขแล้ว เราจะแก้ตัวอย่างความน่าจะเป็นประเภทนี้ทีละขั้นตอนเพื่อทำความเข้าใจความหมายของมันอย่างถ่องแท้
- หลังจากสอบในชั้นเรียนที่มีนักเรียน 30 คน จึงได้รวบรวมข้อมูลเพื่อดูว่ามีนักเรียนกี่คนที่เรียนและกี่คนที่สอบผ่าน ผลลัพธ์แสดงอยู่ในตารางฉุกเฉินต่อไปนี้ จากข้อมูลที่รวบรวมมา ให้คำนวณความน่าจะเป็นแบบมีเงื่อนไขในการผ่านการสอบ หากคุณได้ศึกษามาแล้ว
เพื่อให้ได้ความน่าจะเป็นแบบมีเงื่อนไข เราต้องใช้สูตรที่เราเห็นก่อนหน้านี้:
ดังนั้นเราจึงต้องหาความน่าจะเป็นที่นักเรียนคนใดคนหนึ่งเรียนและผ่าน ในการค้นหาความน่าจะเป็นที่นักเรียนคนหนึ่งเรียน เราเพียงแค่ต้องใช้กฎของลาปลาซ นั่นคือ เราหารจำนวนนักเรียนที่เรียนด้วยจำนวนการสังเกตทั้งหมด:
และเราสามารถหาความน่าจะเป็นที่นักเรียนที่เรียนและสอบผ่านพร้อมๆ กันจากตารางฉุกเฉินได้โดยการหารจำนวนนักเรียนที่เรียนและสอบผ่านด้วยผลรวม:
ดังนั้น ความน่าจะเป็นที่นักเรียนจะสอบผ่านหากได้เรียนไปแล้วคือ:
![\begin{aligned}P(\text{aprobado}|\text{estudiado})&=\cfrac{P(\text{aprobado}\cap\text{estudiado})}{P(\text{estudiado})}\\ &=\cfrac{0,63}{0,77}\\[1.5ex] &=0,82\end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-b93263fb386c7978bd9b5cf886b47377_l3.png "Rendered by QuickLaTeX.com")
ความน่าจะเป็นแบบมีเงื่อนไขของเหตุการณ์ขึ้นอยู่กับและเป็นอิสระ
ในส่วนนี้ เราจะดูว่าความสัมพันธ์ระหว่างความน่าจะเป็นแบบมีเงื่อนไขกับเหตุการณ์ขึ้นอยู่กับและเป็นอิสระ (หรือเหตุการณ์ขึ้นอยู่กับและเป็นอิสระ) เพราะถึงแม้จะเป็นแนวคิดที่แตกต่างกัน แต่เหตุการณ์ทั้งสองประเภทนี้เชื่อมโยงกับความน่าจะเป็นแบบมีเงื่อนไข
สองเหตุการณ์ (หรือเหตุการณ์) เป็นอิสระต่อกันเมื่อความน่าจะเป็นที่จะเกิดขึ้นไม่ได้ขึ้นอยู่กับอีกเหตุการณ์หนึ่ง ในกรณีเช่นนี้ จุดตัดกันระหว่างสองเหตุการณ์จะเท่ากับผลคูณของความน่าจะเป็นของแต่ละเหตุการณ์แยกจากกัน ดังนั้นสูตรความน่าจะเป็นแบบมีเงื่อนไขจึงทำให้ง่ายขึ้น:
กล่าวโดยสรุป หากเหตุการณ์ A และ B เป็นอิสระจากกัน ความน่าจะเป็นแบบมีเงื่อนไขของเหตุการณ์ A ที่กำหนดให้กับเหตุการณ์ B จะเท่ากับความน่าจะเป็นที่เหตุการณ์ A จะเกิดขึ้นทุกประการ
ในทางกลับกัน เมื่อเหตุการณ์สองเหตุการณ์ขึ้นอยู่กับเหตุการณ์หนึ่ง หมายความว่าความน่าจะเป็นของเหตุการณ์หนึ่งจะขึ้นอยู่กับความน่าจะเป็นของอีกเหตุการณ์หนึ่ง ดังนั้น เมื่อเหตุการณ์ A และ B ขึ้นต่อกัน ความน่าจะเป็นแบบมีเงื่อนไขของเหตุการณ์ A ที่ได้รับจากเหตุการณ์ B จะแตกต่างจากความน่าจะเป็นที่เหตุการณ์ A จะเกิดขึ้น
แก้แบบฝึกหัดความน่าจะเป็นแบบมีเงื่อนไข
แบบฝึกหัดที่ 1
เรารู้ว่าในถุงที่เต็มไปด้วยลูกบอล ครึ่งหนึ่งเป็นสีส้ม และอีกครึ่งหนึ่งเป็นสีเขียว นอกจากนี้หนึ่งในสามของลูกบอลทั้งหมดยังเป็นสีส้มและมีป้ายกำกับไว้ในเวลาเดียวกัน ความน่าจะเป็นที่เมื่อคุณวาดลูกบอลสีส้ม มันจะรับสัญญาณเป็นเท่าไร?
เพื่อแก้แบบฝึกหัด เราต้องใช้ความน่าจะเป็นของสูตรตามเงื่อนไข ซึ่งก็คือ:
คำชี้แจงปัญหาบอกเราว่าครึ่งหนึ่งของถุงเป็นส้ม ดังนั้น ความน่าจะเป็นทางทฤษฎีที่จะหยิบลูกบอลสีส้มขึ้นมาคือ 50%
ในทางกลับกัน เรารู้ว่าหนึ่งในสามของทั้งหมดเป็นลูกบอลสีส้มและมีสัญญาณ ดังนั้นความน่าจะเป็นที่จะได้ลูกบอลสีส้มพร้อมสัญญาณคือ:
สุดท้าย เราแทนที่ความน่าจะเป็นที่คำนวณได้ลงในสูตรความน่าจะเป็นแบบมีเงื่อนไขเพื่อค้นหาค่าของมัน:
![\begin{aligned}P(\text{se\~nal}|\text{naranja})&=\cfrac{P(\text{se\~nal}\cap\text{naranja})}{P(\text{naranja})}\\ &=\cfrac{0,33}{0,5}\\[1.5ex] &=0,66\end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-66a7a5e06952a839c7d76ee5555b3400_l3.png "Rendered by QuickLaTeX.com")
สรุปความน่าจะเป็นที่จะได้ลูกบอลที่มีสัญญาณถ้าเป็นสีส้มคือ 66%
แบบฝึกหัดที่ 2
หากเรามีปากกาสีน้ำเงินหกด้ามและปากกาสีดำสามด้ามในกล่อง ให้คำนวณความน่าจะเป็นที่จะวาดปากกาสีน้ำเงินอันเดียวและความน่าจะเป็นที่จะวาดปากกาสีน้ำเงินสองอันติดต่อกัน
หากต้องการทราบความน่าจะเป็นที่จะหยิบปากกาสีน้ำเงินหนึ่งครั้ง เพียงใช้กฎของลาปลาซ:
ปัญหายังขอให้เราทราบความน่าจะเป็นที่จะหยิบปากกาสีน้ำเงินสองอันติดต่อกัน นั่นคือความน่าจะเป็นแบบมีเงื่อนไขในการหยิบปากกาสีน้ำเงิน ถ้าเราเคยหยิบปากกาสีน้ำเงินมาก่อน
หากเราวาดปากกาสีน้ำเงิน แสดงว่ามีกรณีที่ถูกใจน้อยกว่า แต่ก็มีปากกาน้อยกว่าหนึ่งอันในจำนวนทั้งหมดด้วย ความน่าจะเป็นแบบมีเงื่อนไขจึงเป็นดังนี้:
แบบฝึกหัดที่ 3
ความน่าจะเป็นแบบมีเงื่อนไขของการทอยลูกเต๋าเป็นเลข 4 คืออะไร เมื่อพิจารณาจากการทอยเหรียญแล้วได้หัว?
ในการแก้ปัญหาแบบฝึกหัดนี้ คุณต้องคำนึงถึงทฤษฎีความน่าจะเป็นแบบมีเงื่อนไข เนื่องจากเหตุการณ์ “ได้เลข 4 ด้วยการโยนลูกเต๋า” และ “ได้หัวด้วยการโยนเหรียญ” เป็นอิสระจากกัน ดังนั้นจึงไม่จำเป็นต้องใช้สูตรความน่าจะเป็นแบบมีเงื่อนไข แต่จะได้ความเท่าเทียมกันดังต่อไปนี้:
ดังนั้น หากต้องการค้นหาความน่าจะเป็นแบบมีเงื่อนไข เพียงใช้กฎของลาปลาซ:
แบบฝึกหัดที่ 4
มีการศึกษาปีการเงินของบริษัท 25 แห่งในประเทศหนึ่ง และราคาหุ้นของบริษัทเปลี่ยนแปลงอย่างไรโดยขึ้นอยู่กับผลลัพธ์ทางเศรษฐกิจของปีนั้น คุณสามารถดูข้อมูลที่รวบรวมได้ในตารางฉุกเฉินต่อไปนี้:
ราคาหุ้นของบริษัทมีแนวโน้มที่จะเพิ่มขึ้นมากเพียงใดหากทำกำไรได้ในปีที่ผ่านมา?
แบบฝึกหัดนี้ถามเราเกี่ยวกับความน่าจะเป็นแบบมีเงื่อนไขที่หุ้นจะขึ้น เนื่องจากบริษัทบรรลุผลทางเศรษฐกิจที่เป็นบวก ดังนั้น ในการคำนวณความน่าจะเป็นนี้ เราต้องใช้สูตรความน่าจะเป็นแบบมีเงื่อนไข:
ดังนั้นเราจึงคำนวณความน่าจะเป็นที่บริษัทจะทำกำไรได้เป็นอันดับแรก และประการที่สอง ความน่าจะเป็นที่บริษัทจะทำกำไรทางเศรษฐกิจในขณะที่ราคาต่อหุ้นเพิ่มขึ้น:
จากนั้นเราจะแทนค่าที่พบลงในสูตรและคำนวณความน่าจะเป็นแบบมีเงื่อนไข:
![\begin{aligned}P(\text{precio sube}|\text{beneficio})& =\cfrac{P(\text{precio sube}\cap\text{beneficio})}{P(\text{beneficio})}\\ &= \cfrac{0,4}{0,56}\\[1.5ex]& =0,71 \end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-9fdc17ed2f93c9122e9678f52ed88804_l3.png "Rendered by QuickLaTeX.com")
คุณสมบัติของความน่าจะเป็นแบบมีเงื่อนไข
คุณสมบัติของความน่าจะเป็นแบบมีเงื่อนไขหรือความน่าจะเป็นแบบมีเงื่อนไขมีดังนี้
- ผลรวมของความน่าจะเป็นแบบมีเงื่อนไขของเหตุการณ์ A ที่กำหนดให้กับเหตุการณ์ B บวกกับความน่าจะเป็นแบบมีเงื่อนไขของเหตุการณ์เสริม A ที่กำหนดของเหตุการณ์ B เท่ากับ 1
- หากเหตุการณ์ A เป็นสับเซตของเหตุการณ์ B แล้ว A จะเกิดขึ้นเสมอเมื่อ B เป็นจริง ดังนั้น ความน่าจะเป็นแบบมีเงื่อนไขของเหตุการณ์ A ที่ได้รับจากเหตุการณ์ B ในกรณีเหล่านี้คือ 1
- เมื่อพิจารณาจากเหตุการณ์ที่แตกต่างกันสองเหตุการณ์ ความเท่าเทียมกันต่อไปนี้ในส่วนที่เกี่ยวกับความน่าจะเป็นแบบมีเงื่อนไขจะคงอยู่เสมอ:
เกี่ยวกับผู้แต่ง
ดร.เบนจามิน แอนเดอร์สัน
สวัสดี ฉันชื่อเบนจามิน ศาสตราจารย์สถิติเกษียณอายุแล้ว และผันตัวมาเป็นครูสอนสถิติโดยเฉพาะ ด้วยประสบการณ์และความเชี่ยวชาญที่กว้างขวางในสาขาสถิติ ฉันกระตือรือร้นที่จะแบ่งปันความรู้ของฉันเพื่อเสริมศักยภาพนักเรียนผ่าน Statorials. รู้เพิ่มเติม