วิธีการคำนวณความสัมพันธ์ข้ามใน r

ความสัมพันธ์ข้าม เป็นวิธีการวัดระดับความคล้ายคลึงกันระหว่างอนุกรมเวลาและเวอร์ชันที่ล่าช้าของอนุกรมเวลาอื่น

ความสัมพันธ์ประเภทนี้มีประโยชน์ในการคำนวณเพราะสามารถบอกเราได้ว่าค่าในอนุกรมเวลาหนึ่งเป็นการทำนายค่าในอนาคตในอนุกรมเวลาอื่นหรือไม่ กล่าวอีกนัยหนึ่ง มันสามารถบอกเราว่าอนุกรมเวลาหนึ่งเป็นตัวบ่งชี้ที่สำคัญสำหรับอนุกรมเวลาอื่นหรือไม่

ความสัมพันธ์ประเภทนี้ถูกนำมาใช้ในหลายสาขา ได้แก่:

เศรษฐกิจ: ดัชนีความเชื่อมั่นผู้บริโภค (CCI) ถือเป็นตัวบ่งชี้ชั้นนำของผลิตภัณฑ์มวลรวมภายในประเทศ (GDP) ของประเทศ ตัวอย่างเช่น หาก CCI สูงในเดือนหนึ่ง GDP ก็มีแนวโน้มที่จะสูงขึ้น x เดือนต่อมา

ธุรกิจ: การใช้จ่ายด้านการตลาดมักถือเป็นตัวบ่งชี้ชั้นนำของรายได้ทางธุรกิจในอนาคต ตัวอย่างเช่น หากบริษัทใช้จ่ายเงินจำนวนมากผิดปกติเพื่อการตลาดในหนึ่งไตรมาส รายได้รวมก็ควรจะสูง x ไตรมาสในภายหลัง

ชีววิทยา: มลพิษในมหาสมุทรโดยรวมถือเป็นตัวบ่งชี้ที่สำคัญของประชากรเต่าบางสายพันธุ์ ตัวอย่างเช่น หากมลพิษสูงขึ้นในปีหนึ่งๆ คาดว่าจำนวนเต่าทั้งหมดจะลดลง x ปีต่อมา

ตัวอย่างต่อไปนี้แสดงวิธีคำนวณความสัมพันธ์ข้ามระหว่างอนุกรมเวลาสองอนุกรมใน R

ตัวอย่าง: วิธีคำนวณความสัมพันธ์ข้ามใน R

สมมติว่าเรามีอนุกรมเวลาต่อไปนี้ใน R ซึ่งแสดงการใช้จ่ายทางการตลาดทั้งหมด (เป็นพัน) สำหรับบริษัทหนึ่งๆ รวมถึงรายได้รวม (เป็นพัน) เป็นเวลา 12 เดือนติดต่อกัน:

 #define data
marketing <- c(3, 4, 5, 5, 7, 9, 13, 15, 12, 10, 8, 8)
revenue <- c(21, 19, 22, 24, 25, 29, 30, 34, 37, 40, 35, 30)

เราสามารถคำนวณความสัมพันธ์ข้ามสำหรับแต่ละความล่าช้าระหว่างอนุกรมเวลาสองชุดได้โดยใช้ฟังก์ชัน ccf() ดังนี้

 #calculate cross correlation
ccf(marketing, revenue)

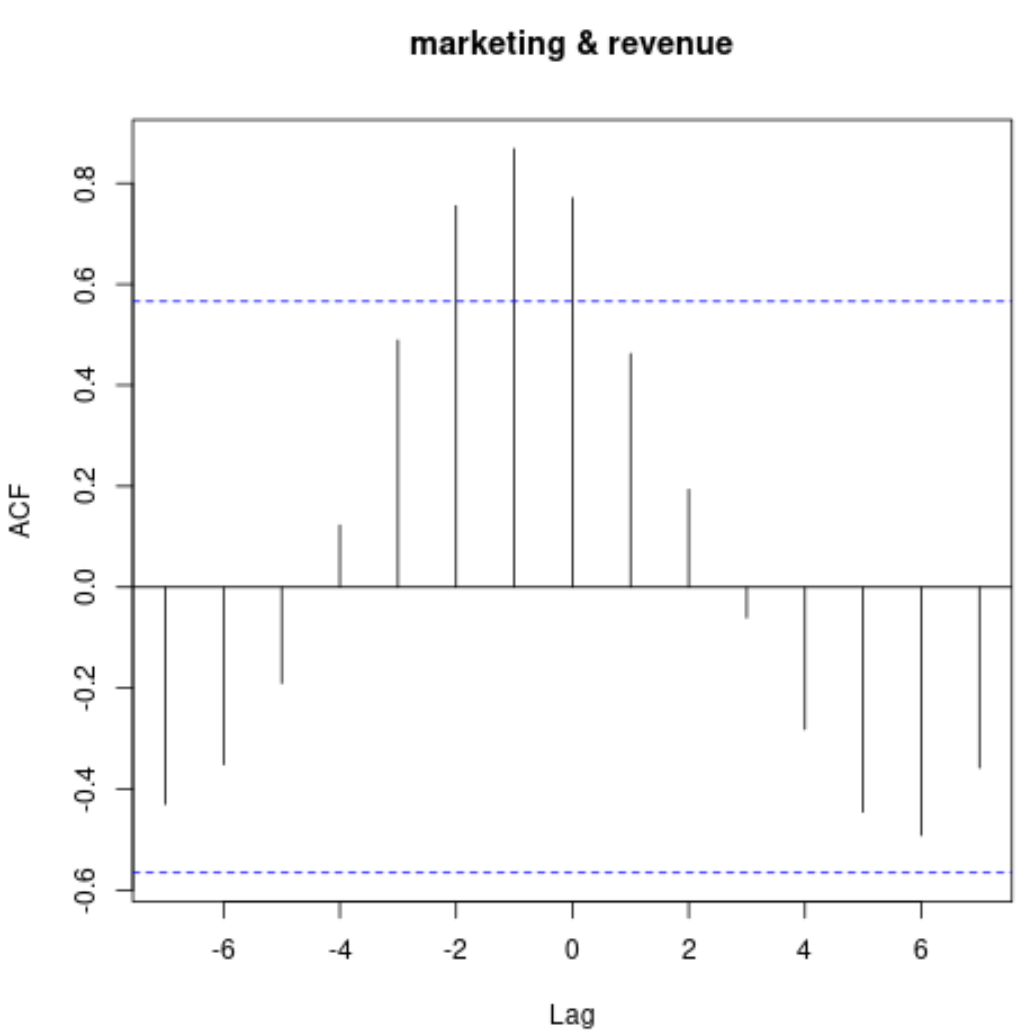
แผนภูมินี้แสดงความสัมพันธ์ระหว่างอนุกรมเวลาสองชุดในช่วงหน่วงที่ต่างกัน

ในการแสดงค่าความสัมพันธ์ที่แท้จริง เราสามารถใช้ไวยากรณ์ต่อไปนี้:

 #display cross correlation values
print (ccf(marketing, revenue))

Autocorrelations of series 'X', by lag

    -7 -6 -5 -4 -3 -2 -1 0 1 2 3 
-0.430 -0.351 -0.190 0.123 0.489 0.755 0.868 0.771 0.462 0.194 -0.061 
     4 5 6 7 
-0.282 -0.445 -0.492 -0.358

ต่อไปนี้เป็นวิธีตีความผลลัพธ์นี้:

• ความสัมพันธ์ข้ามที่ lag 0 คือ 0.771
• ความสัมพันธ์ข้ามที่ความล่าช้า 1 คือ 0.462
• ความสัมพันธ์ข้ามที่ lag 2 คือ 0.194
• ความสัมพันธ์ข้ามที่ lag 3 คือ -0.061

และอื่นๆ

โปรดทราบว่าความสัมพันธ์ระหว่างอนุกรมเวลาทั้งสองนั้นค่อนข้างเป็นบวกโดยมีความล่าช้า -2 ถึง 2 ซึ่งบอกเราว่าการใช้จ่ายด้านการตลาดในเดือนที่กำหนดสามารถคาดการณ์รายได้ได้ค่อนข้างมากในหนึ่งและสองเดือนต่อมา

สิ่งนี้สมเหตุสมผล: เราคาดหวังว่าการใช้จ่ายด้านการตลาดที่สูงในเดือนหนึ่งๆ จะเป็นการคาดการณ์ถึงรายได้ที่เพิ่มขึ้นในอีกสองเดือนข้างหน้า

แหล่งข้อมูลเพิ่มเติม

วิธีการคำนวณความสัมพันธ์อัตโนมัติใน R
วิธีการคำนวณความสัมพันธ์บางส่วนใน R
วิธีการคำนวณความสัมพันธ์แบบเลื่อนใน R