ไม่มีความสัมพันธ์กัน

บทความนี้จะอธิบายว่าตัวแปรสองตัวมีความสัมพันธ์กันเป็นศูนย์หมายความว่าอย่างไร ดังนั้นคุณจะพบตัวอย่างที่ได้รับการแก้ไขแล้วของตัวแปรสุ่มที่ไม่มีความสัมพันธ์กัน และอะไรคือความแตกต่างจากความสัมพันธ์ประเภทอื่น

ความสัมพันธ์เป็นศูนย์คืออะไร?

ในสถิติ ความสัมพันธ์เป็นศูนย์ คือความสัมพันธ์ประเภทหนึ่งระหว่างตัวแปรสองตัวที่แตกต่างกัน แม่นยำยิ่งขึ้น เมื่อตัวแปรสองตัวมีความสัมพันธ์กันเป็นศูนย์ หมายความว่าไม่มีความสัมพันธ์ระหว่างตัวแปรทั้งสอง กล่าวคือ ตัวแปรทั้งสองไม่มีความสัมพันธ์กัน

ในทางคณิตศาสตร์ ความสัมพันธ์เป็นศูนย์จะถูกระบุเนื่องจากค่าสัมประสิทธิ์สหสัมพันธ์เป็นศูนย์ อย่างไรก็ตาม หากค่าของสัมประสิทธิ์สหสัมพันธ์ใกล้กับ 0 มาก โดยทั่วไปจะถือว่ามีความสัมพันธ์เป็นศูนย์เนื่องจากความสัมพันธ์นั้นไม่มีอยู่จริง

หากต้องการเรียนรู้เพิ่มเติมเกี่ยวกับความสัมพันธ์ โปรดไปที่ลิงก์ต่อไปนี้:

ตัวอย่างของความสัมพันธ์เป็นศูนย์

หลังจากดูคำจำกัดความของความสัมพันธ์เป็นศูนย์แล้ว ในส่วนนี้เราจะมาดูตัวอย่างชีวิตประจำวันของตัวแปรสองตัวที่ไม่มีความสัมพันธ์กัน

• จากกลุ่มตัวอย่างจำนวน 20 คน ความสูงและ IQ ของพวกเขา (ใช้ในการวัดความฉลาดของบุคคล) ได้รับการบันทึกไว้ในตารางข้อมูลต่อไปนี้ วิเคราะห์ความสัมพันธ์ระหว่างส่วนสูงและสติปัญญาของบุคคล

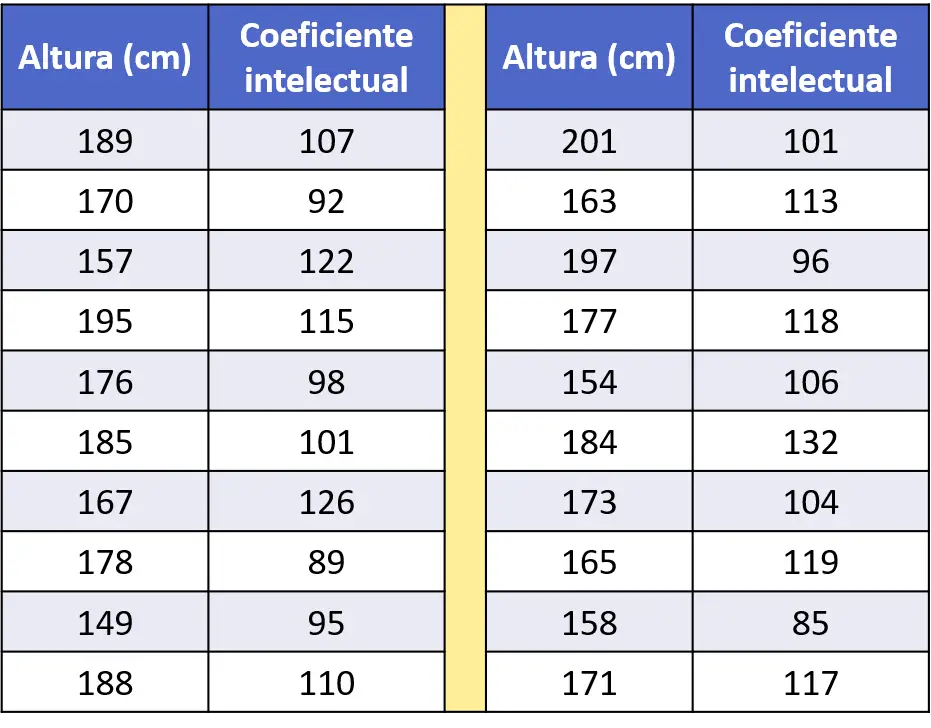
ก่อนอื่น เพื่อศึกษาความสัมพันธ์ระหว่างตัวแปรทางสถิติทั้งสองนี้ เราจำเป็นต้องสร้างกราฟข้อมูล เพื่อให้เรารู้ว่าชุดข้อมูลมีลักษณะอย่างไร ดังนั้นเราจึงสร้างพอยต์คลาวด์:

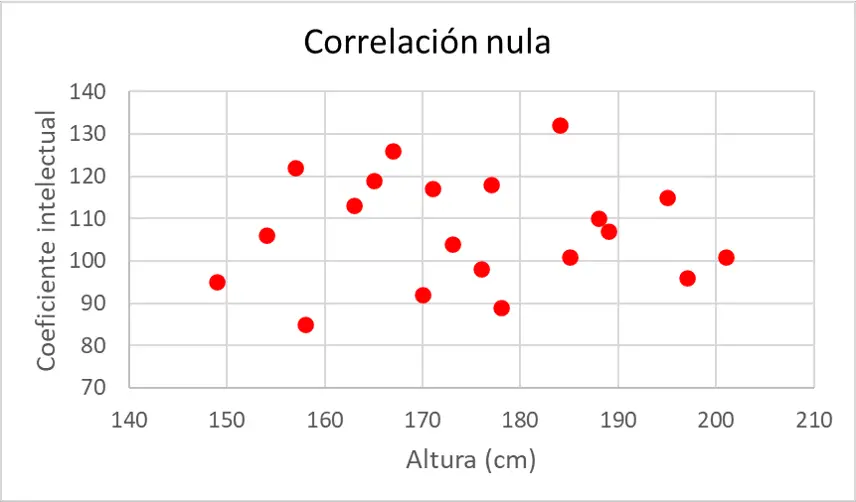
หลังจากสังเกตกราฟแล้ว จะไม่พบความสัมพันธ์แบบนิรนัย เนื่องจากจุดต่างๆ กระจัดกระจายในแผนภาพโดยไม่เป็นไปตามรูปแบบใดๆ

เมื่อเราสร้างกราฟข้อมูลแล้ว เราจะคำนวณค่าสัมประสิทธิ์สหสัมพันธ์แบบเพียร์สัน ซึ่งเป็นค่าสัมประสิทธิ์ที่ระบุระดับความสัมพันธ์ระหว่างตัวแปรสองตัว

ค่าของสัมประสิทธิ์สหสัมพันธ์เพียร์สันอยู่ใกล้กับศูนย์มาก ดังนั้นเราจึงสรุปได้ว่าความสัมพันธ์ระหว่างตัวแปรแบบฝึกหัดทั้งสองนั้นเป็นศูนย์

โปรดทราบว่าเป็นเรื่องยากมากที่ค่าของสัมประสิทธิ์สหสัมพันธ์จะเป็นศูนย์ ดังนั้นคุณต้องตีความตัวเลขที่ได้รับจากแผนภาพกระจาย และวิเคราะห์ว่าความสัมพันธ์ระหว่างตัวแปรทั้งสองนั้นเป็นศูนย์หรือไม่

ความสัมพันธ์เป็นศูนย์ บวก และศูนย์

แม้ว่าบทความนี้จะขึ้นอยู่กับความสัมพันธ์ที่เป็นศูนย์ แต่โปรดทราบว่ายังมีความสัมพันธ์อีกสองประเภท: ความสัมพันธ์เชิงบวกและความสัมพันธ์เชิงลบ ดังนั้นในส่วนสุดท้ายนี้ เราจะเห็นความแตกต่างระหว่างประเภทของความสัมพันธ์

• ความสัมพันธ์เชิงบวก – ตัวแปรหนึ่งจะเพิ่มขึ้นเมื่ออีกตัวแปรหนึ่งเพิ่มขึ้นเช่นกัน ค่าของสัมประสิทธิ์สหสัมพันธ์อยู่ระหว่าง 0 (ไม่รวม) ถึง 1 (รวม)
• ความสัมพันธ์เชิงลบ : เมื่อตัวแปรตัวหนึ่งเพิ่มขึ้น อีกตัวแปรหนึ่งก็จะลดลง และในทางกลับกัน หากตัวแปรตัวหนึ่งลดลง อีกตัวแปรหนึ่งก็จะเพิ่มขึ้น ค่าของสัมประสิทธิ์สหสัมพันธ์อยู่ระหว่าง -1 (รวม) ถึง 0 (ไม่รวม)
• Zero correlation : ไม่มีความสัมพันธ์ระหว่างตัวแปรทั้งสอง ค่าสัมประสิทธิ์สหสัมพันธ์เท่ากับ 0

ในกราฟต่อไปนี้ คุณจะเห็นความสัมพันธ์ประเภทต่างๆ ที่แสดง:

สำหรับข้อมูลเพิ่มเติมเกี่ยวกับความสัมพันธ์แต่ละประเภท คลิกที่นี่: