Heteroskedasticity

บทความนี้จะอธิบายว่าความแตกต่างในสถิติคืออะไร นอกจากนี้ คุณยังจะได้ทราบว่าอะไรเป็นสาเหตุของความต่างจากปกติ ผลที่ตามมาคืออะไร และจะแก้ไขได้อย่างไร

Heteroscedasticity คืออะไร?

ในสถิติ ความแปรปรวนแบบเฮเทอโรสเคดาสติก เป็นคุณลักษณะที่นำเสนอรูปแบบการถดถอยที่บ่งบอกว่าความแปรปรวนของข้อผิดพลาดไม่คงที่ กล่าวอีกนัยหนึ่ง โมเดลเฮเทอโรสเคดาสติกหมายความว่าข้อผิดพลาดมีความแปรปรวนไม่สม่ำเสมอ จากนั้นโมเดลนี้เรียกว่าเฮเทอโรสเคดาสติก

โปรดจำไว้ว่าข้อผิดพลาด (หรือค่าคงเหลือ) ถูกกำหนดให้เป็นความแตกต่างระหว่างมูลค่าจริงและค่าที่ประมาณโดยแบบจำลองการถดถอย

เมื่อสร้างแบบจำลองการถดถอย ข้อผิดพลาดที่เกิดขึ้นจากการสังเกตแต่ละครั้งจะถูกคำนวณโดยใช้นิพจน์ก่อนหน้า ดังนั้น แบบจำลองทางสถิติจึงเป็นแบบเฮเทอโรสซิดาสติก เมื่อ ความแปรปรวน ของข้อผิดพลาดที่คำนวณได้ไม่คงที่ตลอดการสังเกต แต่จะแตกต่างกันไป

แม้ว่ามันอาจจะดูง่ายมาก แต่สิ่งสำคัญคือแบบจำลองการถดถอยต้องไม่แสดงความแตกต่างแบบเฮเทอโรสเคดาสติก เนื่องจากการคำนวณแบบจำลองนั้นขึ้นอยู่กับข้อเท็จจริงที่ว่าความแปรปรวนของค่าคงเหลือนั้นคงที่ อันที่จริง มันเป็นสมมติฐานก่อนหน้านี้ข้อหนึ่งของ แบบจำลองการถดถอย

มีการทดสอบทางสถิติบางอย่างที่สามารถตรวจจับความแตกต่างได้ เช่น การทดสอบสีขาวหรือการทดสอบ Goldfeld-Quandt อย่างไรก็ตาม โดยปกติแล้วโดยการสร้างกราฟส่วนที่เหลือ จะสามารถระบุความเป็นเฮเทอโรสเคดาสติกของพวกมันได้

สาเหตุของความแตกต่าง

สาเหตุที่พบบ่อยที่สุดของความต่างกันในโมเดลคือ:

• เมื่อช่วงข้อมูลกว้างมากเมื่อเทียบกับค่าเฉลี่ย หากในตัวอย่างทางสถิติเดียวกันนั้นมีค่ามากและมีค่าน้อยมากก็มีแนวโน้มว่าแบบจำลองการถดถอยที่ได้รับจะเป็นแบบเฮเทอโรเซดาสติก
• การละเว้นตัวแปรในแบบจำลองการถดถอยยังส่งผลให้เกิดความต่างกันอีกด้วย ตามหลักเหตุผลแล้ว ถ้าตัวแปรที่เกี่ยวข้องไม่รวมอยู่ในแบบจำลอง ความแปรผันของตัวแปรนั้นจะถูกรวมไว้ในส่วนที่เหลือ และไม่จำเป็นต้องได้รับการแก้ไข
• ในทำนองเดียวกัน การเปลี่ยนแปลงโครงสร้างอาจทำให้แบบจำลองไม่เหมาะสมกับชุดข้อมูล ดังนั้น ความแปรปรวนของส่วนที่เหลืออาจไม่คงที่
• เมื่อตัวแปรบางตัวมีค่ามากกว่าตัวแปรอธิบายอื่น ๆ มาก โมเดลอาจมีความต่างศักย์ต่างกัน ในกรณีนี้ ตัวแปรสามารถสัมพันธ์กันเพื่อแก้ไขปัญหาได้

อย่างไรก็ตาม โดยธรรมชาติแล้วบางกรณีมีแนวโน้มที่จะแสดงความแตกต่างที่แตกต่างกัน ตัวอย่างเช่น ถ้าเราจำลองรายได้ของบุคคลด้วยการใช้จ่ายด้านอาหาร คนที่ร่ำรวยกว่าจะมีความแปรปรวนในการใช้จ่ายด้านอาหารมากกว่าคนที่ยากจน เพราะคนรวยบางครั้งกินในร้านอาหารแพงๆ และบางครั้งก็กินในร้านอาหารราคาถูก ไม่เหมือนคนจนที่มักจะกินในร้านอาหารราคาถูก ดังนั้นจึงเป็นเรื่องง่ายสำหรับแบบจำลองการถดถอยที่จะมีความคงทนแบบเฮเทอโรสก์ดาสติก

ผลที่ตามมาของความต่างกัน

โดยหลักแล้ว ผลที่ตามมาของความต่างกันแบบเฮเทอโรสเคดาสติกในแบบจำลองการถดถอยมีดังนี้:

• ประสิทธิภาพจะหายไปในตัวประมาณค่ากำลังสองน้อยที่สุด ซึ่งกำหนดเป็นค่าเฉลี่ยของกำลังสองของข้อผิดพลาด
• เกิดข้อผิดพลาดในการคำนวณ เมทริกซ์ความแปรปรวนร่วม ของตัวประมาณค่ากำลังสองน้อยที่สุด

ความเป็นเฮเทอโรซีดาสติกที่ถูกต้อง

เมื่อผลลัพธ์ของแบบจำลองการถดถอยเป็นแบบเฮเทอโรสซิดาสติก เราสามารถลองแก้ไขต่อไปนี้เพื่อให้ได้ค่าเฮเทอโรสซิดาสติก:

• คำนวณลอการิทึมธรรมชาติของตัวแปรอิสระ ซึ่งโดยทั่วไปจะมีประโยชน์เมื่อความแปรปรวนของส่วนที่เหลือเพิ่มขึ้นในกราฟ
• การเปลี่ยนแปลงประเภทอื่นของตัวแปรอิสระอาจใช้งานได้จริงมากกว่าทั้งนี้ขึ้นอยู่กับพล็อตที่เหลือ ตัวอย่างเช่น หากกราฟอยู่ในรูปพาราโบลา เราสามารถคำนวณกำลังสองของตัวแปรอิสระและเพิ่มตัวแปรนั้นลงในแบบจำลองได้
• ตัวแปรอื่นๆ ยังสามารถใช้สำหรับแบบจำลองได้ การลบหรือเพิ่มตัวแปรจะทำให้ความแปรปรวนของค่าคงเหลือสามารถแก้ไขได้
• แทนที่จะใช้เกณฑ์กำลังสองน้อยที่สุด คุณสามารถใช้เกณฑ์กำลังสองน้อยสุดถ่วงน้ำหนักได้

ความต่างกันและความเป็นเนื้อเดียวกัน

ในที่สุด เราจะเห็นว่าอะไรคือความแตกต่างระหว่างความแตกต่างระหว่างความต่างกันและความเป็นเนื้อเดียวกันในสถิติ เนื่องจากนี่เป็นแนวคิดสองประการของแบบจำลองการถดถอยที่เราต้องเข้าใจให้ชัดเจน

ความเป็นเนื้อเดียวกัน ของแบบจำลองการถดถอยเป็นคุณลักษณะทางสถิติที่บ่งชี้ว่าความแปรปรวนของข้อผิดพลาดคงที่ ดังนั้นแบบจำลองโฮโมสซิดาสติกหมายความว่าความแปรปรวนของข้อผิดพลาดคงที่

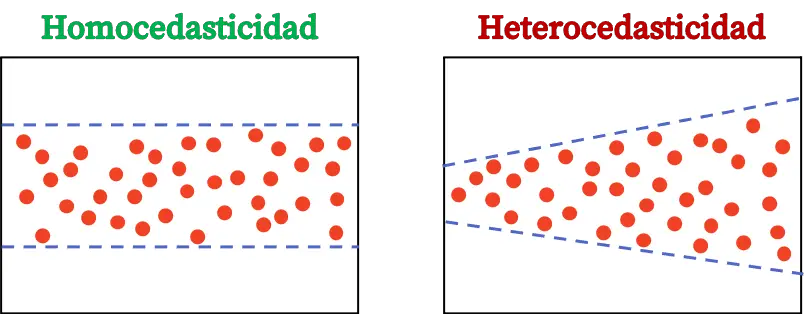
ความแตกต่างระหว่างเฮเทอโรสเคดาสติกซิตี้และโฮโมสเคดาสติกซิตี้ พบได้ในความคงตัวของความแปรปรวนของค่าคงเหลือ ถ้าความแปรปรวนของค่าคงเหลือของแบบจำลองไม่คงที่ หมายความว่าแบบจำลองเป็นแบบเฮเทอโรสซิดาสติก ในทางกลับกัน ถ้าความแปรปรวนของค่าคงเหลือคงที่ นั่นหมายความว่ามันเป็นแบบโฮโมสซิดาสติก

ดังนั้นเราจึงต้องตรวจสอบให้แน่ใจว่าแบบจำลองการถดถอยที่เราสร้างนั้นเป็นแบบโฮโมสซิดาสติก วิธีนี้จะทำให้ได้สมมติฐานที่ว่าความแปรปรวนของค่าคงเหลือคงที่