ช่วงความเชื่อมั่นสำหรับความแตกต่างระหว่างค่าเฉลี่ย

ช่วงความเชื่อมั่น (CI) สำหรับความแตกต่างระหว่างค่าเฉลี่ย คือช่วงของค่าที่มีแนวโน้มว่าจะมีความแตกต่างที่แท้จริงระหว่างค่าเฉลี่ยของประชากรทั้งสองที่มีระดับความเชื่อมั่นในระดับหนึ่ง

บทช่วยสอนนี้จะอธิบายสิ่งต่อไปนี้:

• แรงจูงใจในการสร้างช่วงความมั่นใจนี้
• สูตรการสร้างช่วงความเชื่อมั่นนี้
• ตัวอย่างวิธีคำนวณช่วงความเชื่อมั่นนี้
• วิธีตีความช่วงความมั่นใจนี้

CI สำหรับความแตกต่างระหว่างวิธีการ: แรงจูงใจ

นักวิจัยมักต้องการประมาณความแตกต่างระหว่างค่าเฉลี่ยของประชากรทั้งสอง เพื่อประเมินความแตกต่างนี้ พวกเขาจะสุ่มตัวอย่างจากประชากรแต่ละกลุ่มและคำนวณค่าเฉลี่ยสำหรับแต่ละตัวอย่าง จากนั้นพวกเขาสามารถเปรียบเทียบความแตกต่างระหว่างค่าเฉลี่ยทั้งสองได้

อย่างไรก็ตาม พวกเขาไม่สามารถทราบได้อย่างแน่ชัดว่าความแตกต่างระหว่างค่าเฉลี่ยของกลุ่มตัวอย่างสอดคล้องกับความแตกต่างที่แท้จริงระหว่างค่าเฉลี่ยประชากรหรือไม่ นี่คือเหตุผลที่พวกเขาสามารถสร้าง ช่วงความมั่นใจ สำหรับความแตกต่างระหว่างทั้งสองค่าเฉลี่ยได้ นี่เป็นช่วงของค่าที่น่าจะมีความแตกต่างที่แท้จริงระหว่างค่าเฉลี่ยประชากร

ตัวอย่างเช่น สมมติว่าเราต้องการประมาณค่าความแตกต่างของน้ำหนักเฉลี่ยระหว่างเต่าสองสายพันธุ์ที่แตกต่างกัน เนื่องจากมีเต่าหลายพันตัวในแต่ละประชากร จึงอาจใช้เวลานานและมีราคาแพงเกินไปในการชั่งน้ำหนักเต่าแต่ละตัวทีละตัว

แต่เราอาจ สุ่มตัวอย่าง เต่า 15 ตัวจากแต่ละประชากร และใช้น้ำหนักเฉลี่ยของแต่ละตัวอย่างเพื่อประมาณความแตกต่างที่แท้จริงของน้ำหนักเฉลี่ยระหว่างประชากรทั้งสอง:

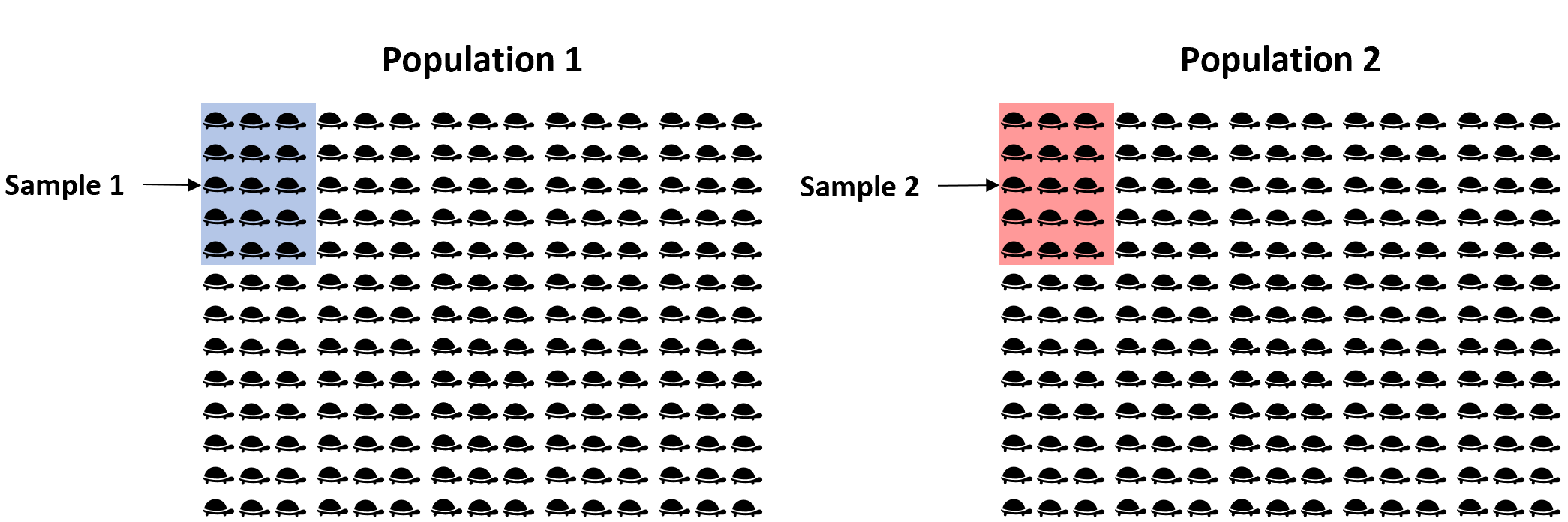
ปัญหาคือว่ากลุ่มตัวอย่างของเราจะสุ่ม ดังนั้นจึงไม่สามารถรับประกันได้ว่าความแตกต่างของน้ำหนักเฉลี่ยระหว่างสองตัวอย่างจะตรงกับความแตกต่างของน้ำหนักเฉลี่ยระหว่างประชากรทั้งสองทุกประการ ดังนั้น เพื่อจับความไม่แน่นอนนี้ เราสามารถสร้างช่วงความเชื่อมั่นที่มีช่วงของค่าที่น่าจะมีความแตกต่างที่แท้จริงในน้ำหนักเฉลี่ยระหว่างประชากรทั้งสอง

CI สำหรับความแตกต่างระหว่างค่าเฉลี่ย: สูตร

เราใช้สูตรต่อไปนี้เพื่อคำนวณช่วงความเชื่อมั่นสำหรับความแตกต่างระหว่างสองวิธี:

ช่วงความเชื่อมั่น = ( x ₁ – x ₂ ) +/- t*√((s _p ² /n ₁ ) + (s _p ² /n ₂ ))

ทอง:

• x ₁ , x ₂ : ค่าเฉลี่ยของกลุ่มตัวอย่าง 1, ค่าเฉลี่ยของกลุ่มตัวอย่าง 2
• t: ค่า t-critical ขึ้นอยู่กับระดับความเชื่อมั่นและระดับความเป็นอิสระ (n ₁ + n ₂ -2)
• _sp ² : ความแปรปรวนรวม
• n ₁ , n ₂ : ขนาดตัวอย่าง 1, ขนาดตัวอย่าง 2

ทอง:

• ความแปรปรวนรวมถูกคำนวณดังนี้: _sp ² = ((n ₁ -1)s ₁ ² + (n ₂ -1)s ₂ ² ) / (n ₁ +n ₂ -2)
• ค่าวิกฤต t สามารถพบได้โดยใช้เครื่องคำนวณการแจกแจงค่า t แบบผกผัน

CI สำหรับความแตกต่างระหว่างค่าเฉลี่ย: ตัวอย่าง

สมมติว่าเราต้องการประมาณค่าความแตกต่างของน้ำหนักเฉลี่ยระหว่างเต่าสองสายพันธุ์ที่แตกต่างกัน เราจึงจะสุ่มตัวอย่างเต่าจำนวน 15 ตัวจากประชากรแต่ละกลุ่ม นี่คือข้อมูลสรุปสำหรับแต่ละตัวอย่าง:

ตัวอย่างที่ 1:

• x1 = ₃₁₀
• ส ₁ = 18.5
• ไม่มี ₁ = 15

ตัวอย่างที่ 2:

• x2 ₌ 300
• _s2 = 16.4
• _n2 = 15

ต่อไปนี้เป็นวิธีค้นหาช่วงความเชื่อมั่นที่แตกต่างกันสำหรับความแตกต่างที่แท้จริงของน้ำหนักเฉลี่ยประชากร:

ช่วงความเชื่อมั่น 90%:

(310-300) +/- 1.70*√((305.61/15) + (305.61/15)) = [-0.8589, 20.8589]

ช่วงความเชื่อมั่น 95%:

(310-300) +/- 2.05*√((305.61/15) + (305.61/15)) = [-3.0757, 23.0757]

ช่วงความมั่นใจ 99%:

(310-300) +/- 2.76*√((305.61/15) + (305.61/15)) = [-7.6389, 27.6389]

หมายเหตุ: คุณยังสามารถค้นหาช่วงความเชื่อมั่นเหล่านี้ได้โดยใช้ ช่วงความเชื่อมั่นทางสถิติสำหรับความแตกต่างระหว่างเครื่องคำนวณค่าเฉลี่ย

คุณจะสังเกตได้ว่ายิ่งระดับความเชื่อมั่นสูง ช่วงความเชื่อมั่นก็จะยิ่งกว้างขึ้น นี่น่าจะสมเหตุสมผล เพราะช่วงที่กว้างกว่ามีแนวโน้มที่จะมีค่าเฉลี่ยประชากรที่แท้จริง ดังนั้นเราจึง “มั่นใจ” มากกว่าว่าช่วงนั้นประกอบด้วยค่าเฉลี่ยประชากรที่แท้จริง

CI สำหรับความแตกต่างระหว่างวิธีการ : การตีความ

วิธีที่เราตีความช่วงความเชื่อมั่นคือ:

มีโอกาส 95% ที่ช่วงความเชื่อมั่นที่ [-3.0757, 23.0757] จะมีความแตกต่างที่แท้จริงของน้ำหนักเฉลี่ยระหว่างประชากรเต่าทั้งสอง

เนื่องจากช่วงเวลานี้มีค่า “0” ซึ่งหมายความว่าจึงเป็นไปได้ว่าน้ำหนักเฉลี่ยของเต่าทั้งสองกลุ่มนี้ไม่มีความแตกต่างกัน กล่าวอีกนัยหนึ่ง เราไม่สามารถพูดด้วยความมั่นใจ 95% ว่ามีน้ำหนักเฉลี่ยที่แตกต่างกันระหว่างเต่าจากประชากรทั้งสองนี้