ความแปรปรวนร่วม

โดย ดร.เบนจามิน แอนเดอร์สัน สิงหาคม 5, 2023 สถิติ 0 ความคิดเห็น

บทความนี้จะอธิบายว่าความแปรปรวนร่วมคืออะไรและคำนวณอย่างไร คุณจะพบสูตรความแปรปรวนร่วมตลอดจนตัวอย่างการคำนวณความแปรปรวนร่วมของชุดข้อมูล นอกจากนี้ คุณยังสามารถคำนวณความแปรปรวนร่วมของชุดข้อมูลใดๆ ได้ด้วยเครื่องคิดเลขออนไลน์ในตอนท้าย

ความแปรปรวนร่วมคืออะไร?

ในสถิติ ความแปรปรวนร่วม คือค่าที่ระบุระดับของการแปรผันร่วมของตัวแปรสุ่มสองตัว กล่าวอีกนัยหนึ่ง ความแปรปรวนร่วมถูกใช้เพื่อวิเคราะห์การพึ่งพาระหว่างตัวแปรสองตัว

ความแปรปรวนร่วมเท่ากับผลรวมของผลคูณของความแตกต่างระหว่างข้อมูลของตัวแปรทั้งสองและวิธีการตามลำดับหารด้วยจำนวนข้อมูลทั้งหมด

👉 คุณสามารถใช้เครื่องคิดเลขด้านล่างเพื่อคำนวณความแปรปรวนร่วมของชุดข้อมูลใดก็ได้

การตีความค่าความแปรปรวนร่วมนั้นง่ายมาก:

หาก ความแปรปรวนร่วมเป็นบวก หมายความว่ามีการพึ่งพากันระหว่างตัวแปรทั้งสอง ดังนั้นเมื่อตัวแปรตัวหนึ่งมีค่าเพิ่มขึ้น ตัวแปรอีกตัวก็จะเพิ่มขึ้นด้วย และในทางกลับกัน
หาก ความแปรปรวนร่วมเป็นลบ หมายความว่าความสัมพันธ์ระหว่างตัวแปรทั้งสองนั้นเป็นลบ ดังนั้นเมื่อตัวแปรตัวหนึ่งมีค่าเพิ่มขึ้น ตัวแปรอีกตัวหนึ่งก็จะลดลง และในทางกลับกัน
หาก ความแปรปรวนร่วมเป็นศูนย์ (หรือค่าใกล้ศูนย์) แสดงว่าไม่มีความสัมพันธ์ระหว่างตัวแปรทั้งสอง กล่าวอีกนัยหนึ่ง ตัวแปรสุ่มทั้งสองมีความเป็นอิสระจากกัน

วิธีการคำนวณความแปรปรวนร่วม

ในการคำนวณความแปรปรวนร่วมของชุดข้อมูล ต้องดำเนินการขั้นตอนต่อไปนี้:

คำนวณค่าเฉลี่ยของแต่ละตัวแปรแยกกัน
สำหรับแต่ละตัวแปร ให้ค้นหาความแตกต่างระหว่างค่าแต่ละค่ากับค่าเฉลี่ยของตัวแปร
คูณความแตกต่างที่คำนวณในขั้นตอนก่อนหน้าสำหรับจุดข้อมูลแต่ละจุด
รวมผลลัพธ์ทั้งหมดที่ได้รับในขั้นตอนก่อนหน้า
หารด้วยจำนวนข้อมูลทั้งหมด ค่าที่ได้รับคือความแปรปรวนร่วมของชุดข้อมูล

โดยสรุป สูตรคำนวณความแปรปรวนร่วมระหว่างตัวแปรสองตัวมีดังนี้

$Cov(X,Y)=\cfrac{\displaystyle \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y})}{n}$

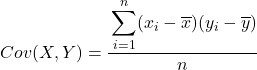
วิธีที่แนะนำเป็นอย่างยิ่งในการแยกความแปรปรวนร่วมระหว่างตัวแปรสองตัวคือการสร้างตารางที่มีคู่ข้อมูลทั้งหมด และเพิ่มคอลัมน์สำหรับแต่ละขั้นตอนที่อธิบายไว้ข้างต้น วิธีนี้จะทำให้การคำนวณของคุณเป็นระเบียบดีขึ้นมากและคุณจะเข้าใจสิ่งที่คุณกำลังทำได้ดีขึ้น

ตัวอย่างการคำนวณความแปรปรวนร่วม

เมื่อพิจารณาคำจำกัดความของความแปรปรวนร่วม ด้านล่างนี้คือตัวอย่างการคำนวณการวัดทางสถิติประเภทนี้ทีละขั้นตอน วัตถุประสงค์คือเพื่อให้คุณเข้าใจแนวคิดเรื่องความแปรปรวนร่วมและวิธีวิเคราะห์ความสัมพันธ์ระหว่างตัวแปรทั้งสองได้ดีขึ้น

คำนวณความแปรปรวนร่วมของชุดข้อมูลทางสถิติต่อไปนี้:

ขั้นแรก เราต้องคำนวณค่าเฉลี่ยเลขคณิตของแต่ละตัวแปร ในการดำเนินการนี้ เราจะหารผลรวมของค่าของแต่ละตัวแปรด้วยจำนวนข้อมูลทั้งหมด

$\overline{x}=\cfrac{58}{10}=5,8$

$\overline{y}=\cfrac{51}{10}=5,1$

➤ ดูที่ ค่าเฉลี่ยสูตรเลขคณิต

เมื่อเราหาค่าเฉลี่ยของตัวแปรสุ่มแต่ละตัวแล้ว เราก็สามารถเพิ่มคอลัมน์ต่อไปนี้ลงในตารางข้อมูลเพื่อรับค่าความแปรปรวนร่วม:

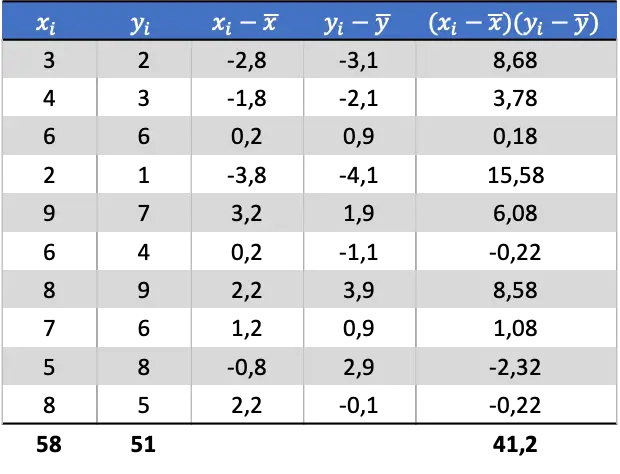
ดังนั้น เพื่อระบุความแปรปรวนร่วมของตัวแปรทั้งสอง คุณต้องหารผลรวมของคอลัมน์สุดท้ายด้วยจำนวนคู่ข้อมูล:

$\begin{aligned}Cov(X,Y)&=\cfrac{\displaystyle \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y})}{n}\\[2ex] Cov(X,Y)&= \cfrac{41,2}{10} \\[2ex]Cov(X,Y)&= 4,12\end{aligned}$

ในกรณีนี้ ค่าความแปรปรวนร่วมเป็นค่าบวก ซึ่งหมายความว่ามีการพึ่งพาโดยตรงระหว่างตัวแปรสุ่มสองตัวที่ศึกษา อย่างไรก็ตาม หากค่าความแปรปรวนร่วมเป็นลบ ก็หมายความว่าการพึ่งพาระหว่างตัวแปรทั้งสองนั้นกลับกัน และสุดท้าย หากค่าความแปรปรวนร่วมเป็นศูนย์หรือใกล้กับศูนย์มาก นั่นหมายความว่าไม่มีความสัมพันธ์เชิงเส้นระหว่างตัวแปรทั้งสอง

ดังที่คุณเห็นจากการแก้ตัวอย่างนี้ การใช้โปรแกรมคอมพิวเตอร์ เช่น Excel เพื่อเพิ่มคอลัมน์ลงในตารางและทำการคำนวณอย่างรวดเร็วจะมีประโยชน์มาก มิฉะนั้น เมื่อคำนวณการดำเนินการด้วยตนเอง จะใช้เวลาในการค้นหาความแปรปรวนร่วมนานกว่ามาก

เครื่องคำนวณความแปรปรวนร่วม

ใส่ชุดข้อมูลทางสถิติลงในเครื่องคิดเลขต่อไปนี้เพื่อคำนวณความแปรปรวนร่วมระหว่างตัวแปรสองตัว คุณต้องแยกคู่ข้อมูลออก เพื่อให้ในกล่องแรกมีเพียงค่าของตัวแปรตัวเดียว และในกล่องที่สองจะมีเพียงค่าของตัวแปรตัวที่สองเท่านั้น

ข้อมูลต้องคั่นด้วยช่องว่างและป้อนโดยใช้จุดเป็นตัวคั่นทศนิยม

คุณสมบัติความแปรปรวนร่วม

ความแปรปรวนร่วมมีคุณสมบัติดังต่อไปนี้:

ความแปรปรวนร่วมระหว่างตัวแปรสุ่มและค่าคงที่เป็นศูนย์

$Cov(X,a)=0$

ความแปรปรวนร่วมของตัวแปรและตัวมันเองนั้นเทียบเท่ากับความแปรปรวนของตัวแปรนั้น

$Cov(X,X)=Var(X)$

➤ ดู: ความแปรปรวนคืออะไร?

ความแปรปรวนร่วมเป็นไปตามคุณสมบัติสมมาตร ดังนั้นความแปรปรวนร่วมของตัวแปร X และ Y จึงเท่ากับความแปรปรวนร่วมของตัวแปร Y และ X ลำดับของตัวแปรไม่ส่งผลต่อผลลัพธ์ของความแปรปรวนร่วม

$Cov(X,Y)=Cov(Y,X)$

หากตัวแปรคูณด้วยค่าคงที่ คุณสามารถคำนวณความแปรปรวนร่วมก่อนแล้วจึงคูณผลลัพธ์ด้วยค่าคงที่

$Cov(a\cdot X,b\cdot Y)=a\cdot b\cdot Cov(X,Y)$

การเพิ่มเงื่อนไขให้กับตัวแปรจะไม่ส่งผลต่อผลลัพธ์ความแปรปรวนร่วม

$Cov(a+X,b+Y)=Cov(X+Y)$

ความแปรปรวนร่วมระหว่างตัวแปรสุ่มสองตัวสัมพันธ์กับความคาดหวังทางคณิตศาสตร์ ความแปรปรวนร่วมระหว่างตัวแปร X และ Y เท่ากับค่าคาดหวังทางคณิตศาสตร์ของผลคูณของ X และ Y ลบด้วยผลคูณของค่าคาดหวังทางคณิตศาสตร์ของตัวแปรแต่ละตัว

$Cov(X,Y)=E[X\cdot Y]-E[X]\cdot E[Y]$

เมื่อดำเนินการกับตัวแปร นิพจน์พีชคณิตต่อไปนี้จะถูกเติมด้วยความเคารพต่อความแปรปรวนร่วม:

$\begin{aligned}\displaystyle Cov(aX+bY,cW+dV)= \ & \displaystyle acCov(X,W)+adCov(X,V)+\\[2ex]& +bcCov(Y,W)+bdCov(Y,V)\end{aligned}$

เกี่ยวกับผู้แต่ง

ดร.เบนจามิน แอนเดอร์สัน

สวัสดี ฉันชื่อเบนจามิน ศาสตราจารย์สถิติเกษียณอายุแล้ว และผันตัวมาเป็นครูสอนสถิติโดยเฉพาะ ด้วยประสบการณ์และความเชี่ยวชาญที่กว้างขวางในสาขาสถิติ ฉันกระตือรือร้นที่จะแบ่งปันความรู้ของฉันเพื่อเสริมศักยภาพนักเรียนผ่าน Statorials. รู้เพิ่มเติม