ช่วงระหว่างควอไทล์ (iqr) ได้รับผลกระทบจากค่าผิดปกติหรือไม่?

ในทางสถิติ เรามักต้องการทราบว่าค่าต่างๆ “กระจาย” ออกไปในการแจกแจงนั้นกว้างเพียงใด

วิธีที่นิยมในการวัดค่าสเปรดคือ ช่วงระหว่างควอร์ไทล์ ซึ่งคำนวณเป็นความแตกต่างระหว่างควอไทล์ที่ 1 และควอไทล์ที่ 3 ของชุดข้อมูล ควอร์ไทล์เป็นเพียงค่าที่แบ่งชุดข้อมูลออกเป็นสี่ส่วนเท่า ๆ กัน

ตัวอย่าง: การคำนวณพิสัยระหว่างควอไทล์

ตัวอย่างต่อไปนี้แสดงวิธีคำนวณช่วงระหว่างควอไทล์สำหรับชุดข้อมูลที่ระบุ:

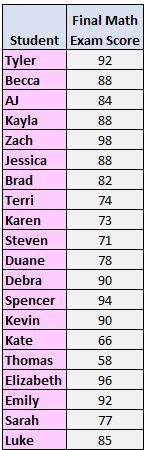
ขั้นตอนที่ 1: จัดเรียงค่าจากน้อยไปหามาก

58, 66, 71, 73, 74, 77, 78, 82, 84, 85, 88, 88, 88, 90, 90, 92, 92, 94, 96, 98

2. ค้นหาค่ามัธยฐาน

58, 66, 71, 73, 74, 77 , 78 , 82 , 84, 85, 88, 88, 88, 90, 90, 92, 92, 94, 96, 98

ในกรณีนี้ ค่ามัธยฐานจะอยู่ระหว่าง 85 ถึง 88

3. ค่ามัธยฐานแบ่งชุดข้อมูลออกเป็นสองซีก ค่ามัธยฐานของครึ่งล่างคือควอไทล์ล่าง และค่ามัธยฐานของครึ่งบนคือควอไทล์บน:

58, 66, 71, 73 , 74 , 77, 78, 82, 84, 85, 88, 88, 88, 90, 90, 92, 92, 94, 96, 98

4. คำนวณพิสัยระหว่างควอไทล์

ในกรณีนี้ ควอไทล์ที่ 1 คือค่าเฉลี่ยของสองค่าตรงกลางในครึ่งล่างของชุดข้อมูล (75.5) และควอไทล์ที่ 3 คือค่าเฉลี่ยของสองค่าตรงกลางในครึ่งบนของชุดข้อมูล (91)

ดังนั้นช่วงระหว่างควอไทล์คือ 91 – 75.5 = 15.5

ช่วงระหว่างควอไทล์ไม่ได้รับผลกระทบจากค่าผิดปกติ

เหตุผลหนึ่งที่ผู้คนชอบใช้ช่วงระหว่างควอไทล์ (IQR) เมื่อคำนวณ “สเปรด” ของชุดข้อมูลก็คือช่วงค่าผิดปกตินั้นทนทาน เนื่องจาก IQR เป็นเพียงช่วงกลางของค่าข้อมูล 50% จึงไม่ได้รับผลกระทบจาก ค่าผิดปกติที่รุนแรง

เพื่อสาธิตสิ่งนี้ ให้พิจารณาชุดข้อมูลต่อไปนี้:

[1, 4, 8, 11, 13, 17, 17, 20]

ต่อไปนี้คือเมตริกการเผยแพร่ต่างๆ สำหรับชุดข้อมูลนี้:

• พิสัยระหว่างควอไทล์: 11
• ระยะ: 19
• ส่วนเบี่ยงเบนมาตรฐาน: 6.26
• ความแตกต่าง: 39.23

ตอนนี้ให้พิจารณาชุดข้อมูลเดียวกันแต่มีค่าผิดปกติที่เพิ่มเข้ามา:

[1, 4, 8, 11, 13, 17, 17, 20, 150 ]

ต่อไปนี้คือเมตริกการเผยแพร่ต่างๆ สำหรับชุดข้อมูลนี้:

• ช่วงระหว่างควอไทล์: 12.5
• ระยะ: 149
• ส่วนเบี่ยงเบนมาตรฐาน: 43.96
• สเปรด: 1,932.84

สังเกตว่าช่วงระหว่างควอไทล์เปลี่ยนแปลงเพียงเล็กน้อยจาก 11 เป็น 12.5 อย่างไรก็ตาม การวัดการกระจายอื่นๆ ทั้งหมดเปลี่ยนแปลงไปอย่างมาก

นี่แสดงให้เห็นว่าพิสัยระหว่างควอไทล์ไม่ได้รับผลกระทบจากค่าผิดปกติ เช่นเดียวกับการวัดการกระจายอื่นๆ ด้วยเหตุนี้ จึงเป็นวิธีที่เชื่อถือได้ในการวัดการกระจายตัวของค่าตรงกลาง 50% ในการแจกแจงใดๆ

อ่านเพิ่มเติม:

การวัดการกระจายตัว
เครื่องคำนวณช่วงระหว่างควอไทล์