ค่าวิกฤต

โดย ดร.เบนจามิน แอนเดอร์สัน สิงหาคม 3, 2023 สถิติ 0 ความคิดเห็น

บทความนี้จะอธิบายว่าค่าวิกฤตในสถิติคืออะไร และควรตีความอย่างไรในการทดสอบสมมติฐาน ในทำนองเดียวกัน คุณจะเห็นวิธีคำนวณค่าวิกฤตพร้อมตัวอย่างที่เป็นรูปธรรมหลายตัวอย่าง

ค่าวิกฤตคืออะไร?

ค่าวิกฤต คือจุดในการกระจายของสถิติการทดสอบที่แยกขอบเขตของการปฏิเสธสมมติฐานว่างออกจากขอบเขตการยอมรับ กล่าวอีกนัยหนึ่ง ค่าวิกฤตคือค่าของการแจกแจงของการทดสอบทางสถิติซึ่งทำเครื่องหมายขีดจำกัดของขอบเขตการปฏิเสธ (หรือขอบเขตวิกฤต)

โดยปกติ ค่าวิกฤติจะแสดงด้วยสัญลักษณ์ Z _α/2 เนื่องจากการแจกแจงอ้างอิงที่พบบ่อยที่สุดมักจะเป็นการ แจกแจงแบบปกติมาตรฐาน

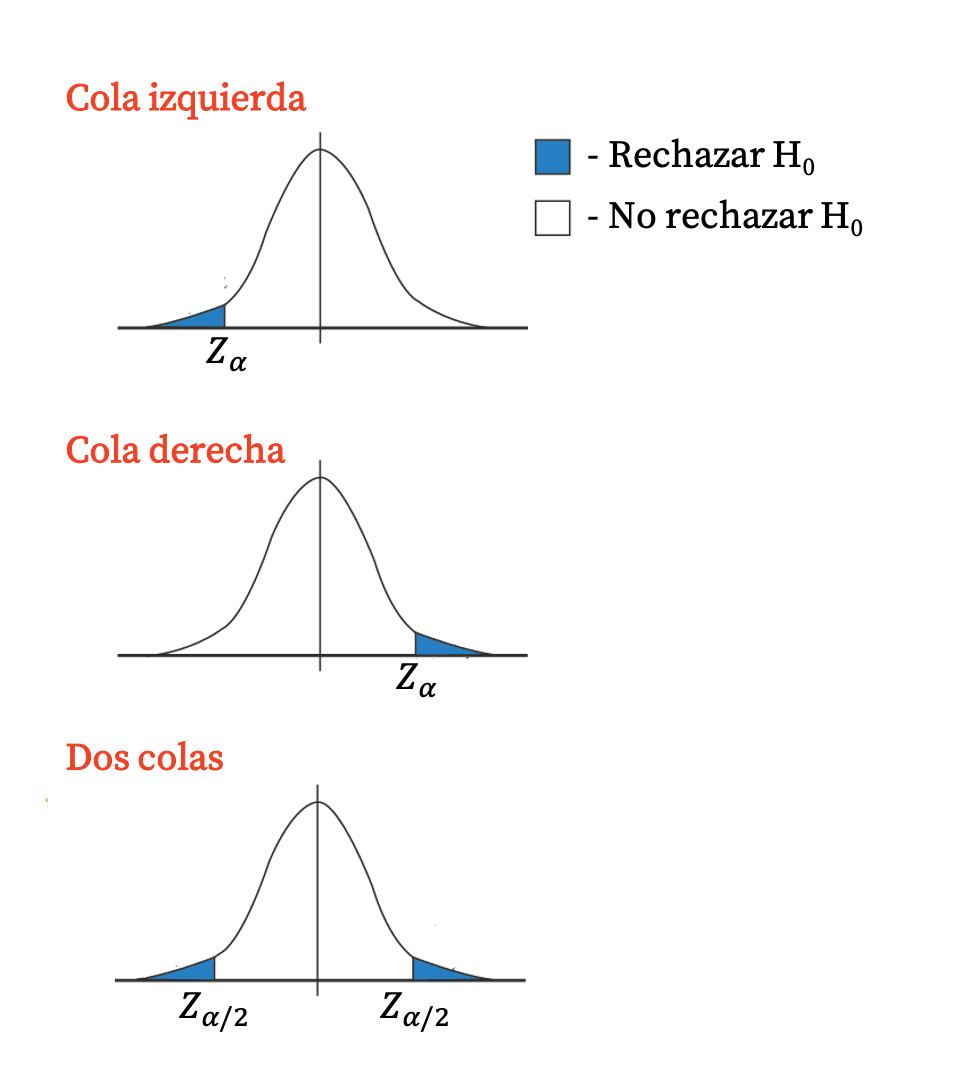
โดยทั่วไป การทดสอบด้านเดียวมีค่าวิกฤต เนื่องจากขอบเขตการปฏิเสธประกอบขึ้นเป็นหางเดียวของการแจกแจง ในทางกลับกัน การทดสอบแบบสองด้านมีค่าวิกฤตสองค่า เนื่องจากขอบเขตการปฏิเสธสอดคล้องกับทั้งสองส่วนของการแจกแจง

ใน ช่วงความเชื่อมั่น ค่าวิกฤตคือจุดในการแจกแจงอ้างอิงที่ทำเครื่องหมายขีดจำกัดของช่วงความเชื่อมั่น

วิธีการคำนวณค่าวิกฤต

จากนั้นเราจะดูว่ามีการคำนวณค่าวิกฤตที่พบบ่อยที่สุดอย่างไร ค่าวิกฤตของ Z และค่าวิกฤตของ t คำนวณสำหรับช่วงความเชื่อมั่นของค่าเฉลี่ย ข้อแตกต่างเพียงอย่างเดียวคือค่าวิกฤตของ Z คำนวณเมื่อทราบค่าเบี่ยงเบนมาตรฐานของประชากร และใช้ค่าวิกฤตของ t แทน เมื่อทราบข้อมูลสำหรับตัวอย่างเดียวเท่านั้น

ค่าวิกฤตของ Z

ค่าวิกฤตของ Z ใช้เพื่อกำหนดขีดจำกัดของช่วงความเชื่อมั่นสำหรับค่าเฉลี่ย พูดให้ถูกคือ ใช้เฉพาะเมื่อคุณทราบค่าเบี่ยงเบนมาตรฐานของประชากรเท่านั้น

ในการ คำนวณค่าวิกฤตของ Z ต้องพบค่าที่สอดคล้องกับความน่าจะเป็นของระดับนัยสำคัญครึ่งหนึ่งใน ตารางการแจกแจงแบบปกติมาตรฐาน

ตัวอย่างเช่น หากเราต้องการหาช่วงความเชื่อมั่นสำหรับค่าเฉลี่ยที่มีระดับความเชื่อมั่น 95% ก็แสดงว่าระดับนัยสำคัญคือ 5% ดังนั้นจึงจำเป็นต้องดูในตารางการแจกแจงแบบปกติมาตรฐานว่าค่าใดสอดคล้องกับความน่าจะเป็นที่ 2.5% เนื่องจากช่วงความเชื่อมั่นของค่าเฉลี่ยเป็นแบบสองด้าน

$1-\alpha=0,95 \ \color{orange}\bm{\longrightarrow}\color{black} \ \alpha=0,05 \ \color{orange}\bm{\longrightarrow}\color{black}\ \alpha/2=0,025$

$\begin{array}{c}Z_{\alpha/2}= \ \color{orange}\bm{?}\\[4ex]Z_{0,025}=1,96\end{array}$

ด้านล่างนี้ คุณจะเห็นตารางที่มีค่า Z วิกฤตที่ใช้มากที่สุด:

ระดับความเชื่อมั่น (1-α)	ระดับนัยสำคัญ (α)	ค่าวิกฤต (Z _α/2 )
0.80	0.20	1,282
0.85	0.15	1,440
0.90	0.10	1,645
0.95	0.05	1960
0.99	0.01	2,576
0.995	0.005	2,807
0.999	0.001	3,291

ค่าวิกฤตของ t

ค่า t วิกฤตใช้เพื่อค้นหาขีดจำกัดของช่วงความเชื่อมั่นของค่าเฉลี่ยเมื่อไม่ทราบค่าเบี่ยงเบนมาตรฐานของประชากร

ใน การคำนวณค่าวิกฤตของ t ค่าที่สอดคล้องกับความน่าจะเป็นของระดับนัยสำคัญครึ่งหนึ่งจะต้องพบใน ตารางการแจกแจง t ของนักเรียน โดยคำนึงถึงระดับความเป็นอิสระของการแจกแจง t ของนักเรียนเป็นหน่วย กว่าขนาดตัวอย่าง

ตัวอย่างเช่น หากเราต้องการค้นหาช่วงความเชื่อมั่นที่มีระดับความเชื่อมั่น 95% และขนาดตัวอย่างคือ 8 เราจำเป็นต้องเข้าถึงตารางการแจกแจง t ของนักเรียน และดูว่าค่าใดสอดคล้องกับ t _0.025|7

$1-\alpha=0,95 \ \color{orange}\bm{\longrightarrow}\color{black} \ \alpha=0,05 \ \color{orange}\bm{\longrightarrow}\color{black}\ \alpha/2=0,025$

$\begin{array}{c}t_{\alpha/2| n-1}= \ \color{orange}\bm{?}\\[4ex]t_{0,025| 7}=2,365\end{array}$

➤ ดู: วิธีคำนวณช่วงความเชื่อมั่นของค่าเฉลี่ย

ค่าวิกฤตในการทดสอบสมมติฐาน

ค่าวิกฤตยังสามารถใช้ในการทดสอบสมมติฐานเพื่อปฏิเสธสมมติฐานว่าง (และยอมรับสมมติฐานทางเลือก) หรือปฏิเสธสมมติฐานทางเลือก (และยอมรับสมมติฐานว่าง)

หากค่าของการแจกแจงของสถิติการทดสอบที่สอดคล้องกับค่า p อยู่ภายในช่วงเวลาที่ทำเครื่องหมายด้วยค่าวิกฤต สมมติฐานว่างจะไม่ถูกปฏิเสธ (สมมติฐานทางเลือกจะถูกปฏิเสธ)
หากค่าของการแจกแจงของสถิติการทดสอบที่สอดคล้องกับค่า p อยู่นอกช่วงเวลาที่ทำเครื่องหมายด้วยค่าวิกฤต สมมติฐานว่างจะถูกปฏิเสธ (ยอมรับสมมติฐานทางเลือก)

เกี่ยวกับผู้แต่ง

ดร.เบนจามิน แอนเดอร์สัน

สวัสดี ฉันชื่อเบนจามิน ศาสตราจารย์สถิติเกษียณอายุแล้ว และผันตัวมาเป็นครูสอนสถิติโดยเฉพาะ ด้วยประสบการณ์และความเชี่ยวชาญที่กว้างขวางในสาขาสถิติ ฉันกระตือรือร้นที่จะแบ่งปันความรู้ของฉันเพื่อเสริมศักยภาพนักเรียนผ่าน Statorials. รู้เพิ่มเติม