คู่มือฉบับสมบูรณ์: วิธีรายงานผลลัพธ์ anova
การวิเคราะห์ความแปรปรวนแบบทางเดียว ใช้เพื่อพิจารณาว่ามีความแตกต่างที่มีนัยสำคัญทางสถิติระหว่างค่าเฉลี่ยของกลุ่มอิสระสามกลุ่มขึ้นไปหรือไม่
เมื่อรายงานผลลัพธ์ของการวิเคราะห์ความแปรปรวนแบบทางเดียว เราจะใช้โครงสร้างทั่วไปต่อไปนี้เสมอ:
- คำอธิบายโดยย่อเกี่ยวกับตัวแปรอิสระและตัวแปรตาม
- ค่า F โดยรวมของ ANOVA และค่า p ที่สอดคล้องกัน
- ผลลัพธ์ของการเปรียบเทียบภายหลัง (หากค่า p มีนัยสำคัญทางสถิติ)
นี่คือถ้อยคำที่เราสามารถใช้ได้:
ทำการวิเคราะห์ความแปรปรวนแบบทางเดียวเพื่อเปรียบเทียบผลของ [ตัวแปรอิสระ] ต่อ [ตัวแปรตาม]
การวิเคราะห์ความแปรปรวนทางเดียวเปิดเผยว่า [มีหรือไม่มี] ความแตกต่างที่มีนัยสำคัญทางสถิติใน [ตัวแปรตาม] ระหว่างอย่างน้อยสองกลุ่ม (F (ระหว่างกลุ่ม df ภายในกลุ่ม df) = [ค่า F], p = [p – ค่า]).
การทดสอบ HSD ของ Tukey สำหรับการเปรียบเทียบหลายรายการพบว่าค่าเฉลี่ยของ [ตัวแปรตาม] แตกต่างกันอย่างมีนัยสำคัญระหว่าง [ชื่อกลุ่ม] และ [ชื่อกลุ่ม] (p = [p-value], 95% CI = [ต่ำกว่า, เหนือกว่า])
ไม่มีความแตกต่างที่มีนัยสำคัญทางสถิติระหว่าง [ชื่อกลุ่ม] และ [ชื่อกลุ่ม] (p = [p-value])
ตัวอย่างต่อไปนี้แสดงวิธีการรายงานผลลัพธ์ของการวิเคราะห์ความแปรปรวนแบบทางเดียวในทางปฏิบัติ
ตัวอย่าง: การรายงานผลลัพธ์ของการวิเคราะห์ความแปรปรวนแบบทางเดียว
สมมติว่านักวิจัยรับสมัครนักศึกษาจำนวน 30 คนเพื่อเข้าร่วมการศึกษาวิจัย นักเรียนจะถูกสุ่มให้ใช้หนึ่งในสามเทคนิคการเรียนในเดือนถัดไปเพื่อเตรียมตัวสอบ สิ้นเดือน นักเรียนทุกคนจะสอบแบบเดียวกัน
จากนั้นผู้วิจัยจะทำการวิเคราะห์ความแปรปรวนแบบทางเดียวเพื่อตรวจสอบว่าคะแนนสอบเฉลี่ยระหว่างทั้งสามกลุ่มมีความแตกต่างกันหรือไม่
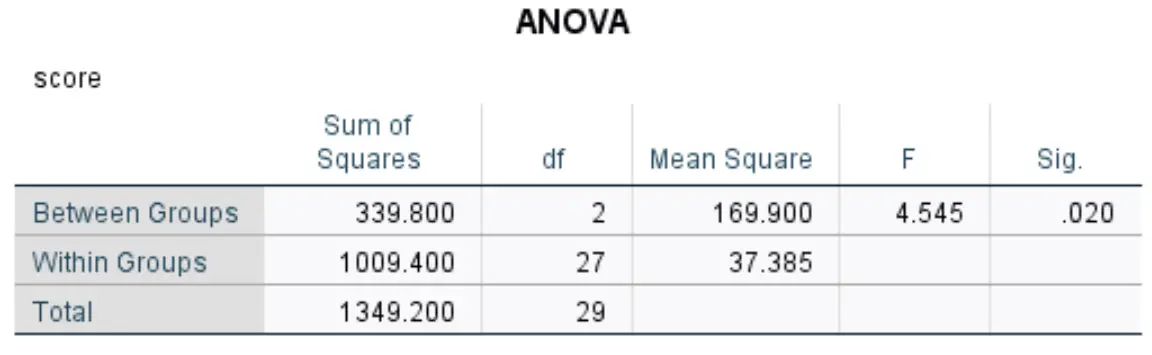
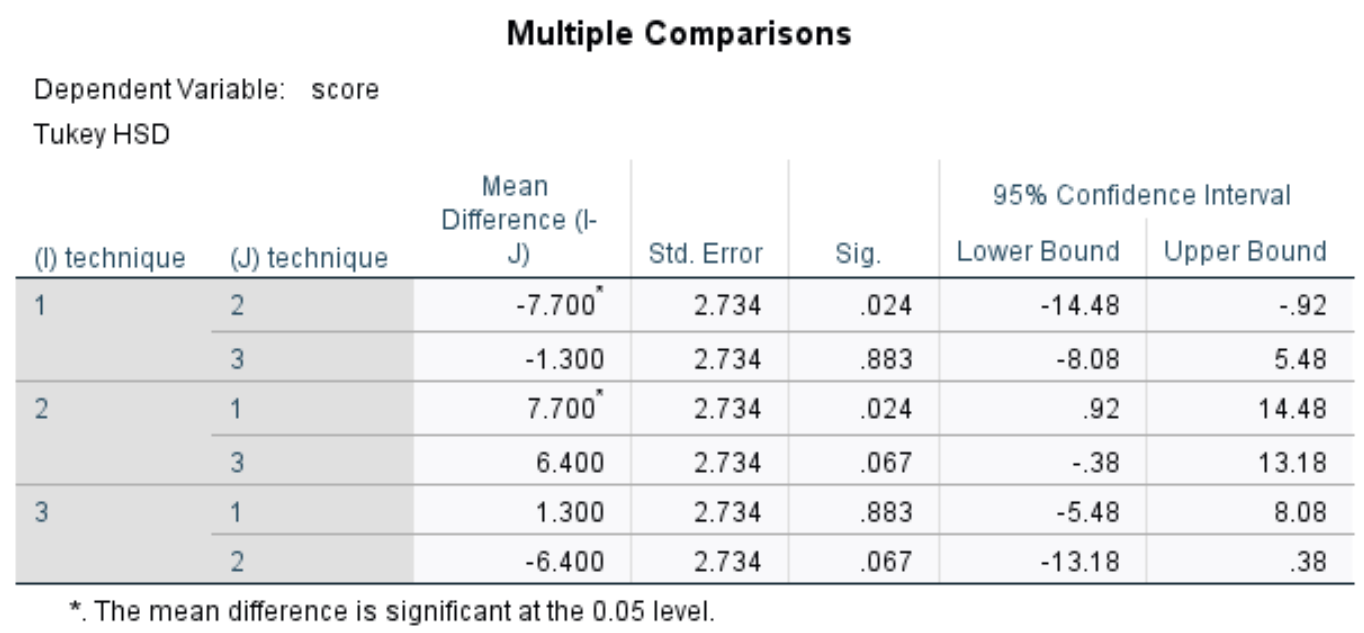
ตารางต่อไปนี้นำเสนอผลลัพธ์ของการวิเคราะห์ความแปรปรวนแบบทางเดียวและตารางเปรียบเทียบหลายรายการหลังการแก้ไขของ Tukey:
ต่อไปนี้เป็นวิธีรายงานผลลัพธ์ ANOVA แบบทางเดียว:
ทำการวิเคราะห์ความแปรปรวนทางเดียวเพื่อเปรียบเทียบผลของเทคนิคการศึกษาที่แตกต่างกันสามเทคนิคต่อผลการทดสอบ
การวิเคราะห์ความแปรปรวนแบบทางเดียวเปิดเผยว่ามีความแตกต่างที่มีนัยสำคัญทางสถิติในคะแนนสอบเฉลี่ยระหว่างอย่างน้อยสองกลุ่ม (F(2,27) = [4.545], p = 0.02)
การทดสอบ HSD ของ Tukey สำหรับการเปรียบเทียบหลายรายการพบว่าค่าเฉลี่ยของคะแนนสอบแตกต่างกันอย่างมีนัยสำคัญระหว่างเทคนิคที่ 1 และเทคนิคที่ 2 (p = 0.024, 95% CI = [-14.48, -0.92])
ไม่มีความแตกต่างอย่างมีนัยสำคัญทางสถิติในคะแนนสอบเฉลี่ยระหว่างเทคนิคที่ 1 และเทคนิคที่ 3 (p = 0.883) หรือระหว่างเทคนิคที่ 2 และเทคนิคที่ 3 (p = 0.067)
สิ่งที่ควรคำนึงถึง
ต่อไปนี้คือสิ่งที่ควรคำนึงถึงเมื่อรายงานผลลัพธ์ของการวิเคราะห์ความแปรปรวนแบบทางเดียว:
ใช้ตารางสถิติเชิงพรรณนา
อาจเป็นประโยชน์ในการนำเสนอตารางสถิติเชิงพรรณนาที่แสดงค่าเฉลี่ยและส่วนเบี่ยงเบนมาตรฐานของค่าในแต่ละกลุ่มการรักษาเพื่อให้ผู้อ่านเห็นภาพข้อมูลที่สมบูรณ์ยิ่งขึ้น
ตัวอย่างเช่น SPSS จัดทำตารางสถิติเชิงพรรณนาต่อไปนี้ซึ่งแสดงค่าเฉลี่ยและส่วนเบี่ยงเบนมาตรฐานของคะแนนสอบสำหรับนักเรียนในแต่ละกลุ่มทักษะการเรียนทั้งสามกลุ่ม:
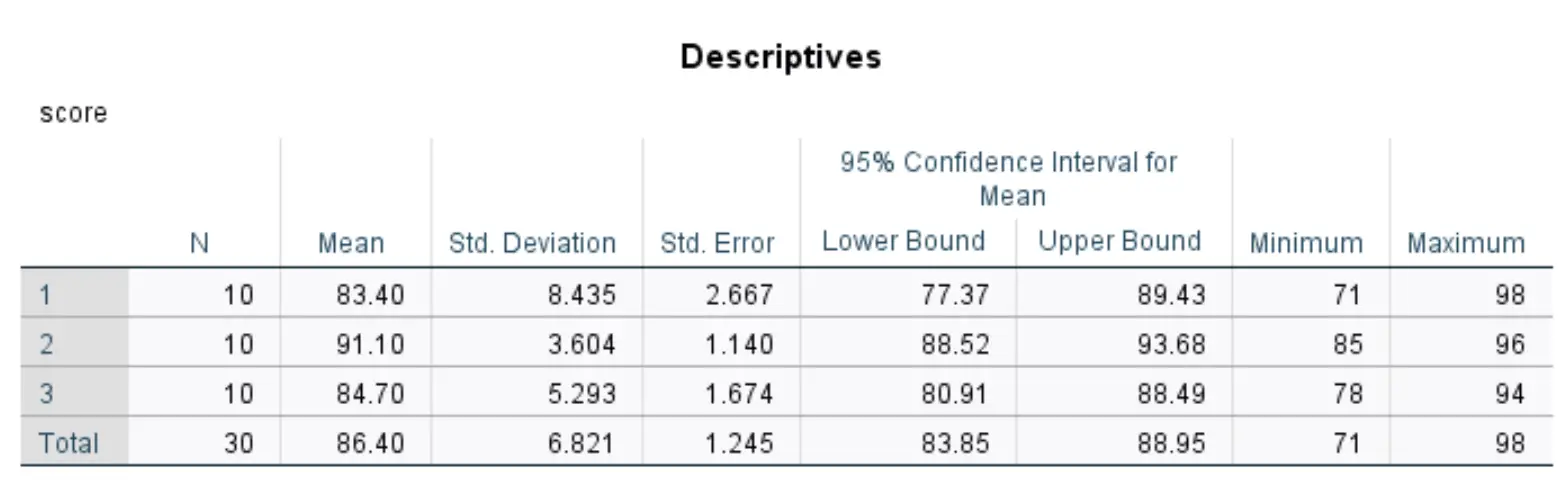
รายงานผลหลังการรักษาเฉพาะในกรณีที่จำเป็นเท่านั้น
หากค่า p-value โดยรวมของ ANOVA ไม่มีนัยสำคัญทางสถิติ คุณจะไม่ทำการเปรียบเทียบหลายรายการภายหลังเฉพาะกิจระหว่างกลุ่ม ซึ่งหมายความว่าคุณไม่จำเป็นต้องรายงานผลลัพธ์หลังการดำเนินการในรายงานขั้นสุดท้ายอย่างชัดเจน
หากคุณต้องการทำการทดสอบหลังการทดสอบ โดยทั่วไปจะใช้การทดสอบ Tukey HSD แต่บางครั้งคุณสามารถใช้ การทดสอบ Scheffe หรือ Bonferroni แทนได้
ปัดเศษค่า p หากจำเป็น
โดยทั่วไปแล้ว ค่า F โดยรวมและค่า p ทั้งหมดในผลลัพธ์ ANOVA จะถูกปัดเศษเป็นทศนิยมสองหรือสามตำแหน่งเพื่อความกระชับ
ไม่ว่าคุณจะเลือกใช้ทศนิยมจำนวนเท่าใด อย่าลืมให้สอดคล้องกันตลอดทั้งรายงาน
แหล่งข้อมูลเพิ่มเติม
บทช่วยสอนต่อไปนี้จะอธิบายวิธีรายงานการทดสอบและขั้นตอนทางสถิติอื่นๆ ในรูปแบบ APA:
วิธีรายงานผลลัพธ์การวิเคราะห์ความแปรปรวนแบบสองทาง (พร้อมตัวอย่าง)
วิธีรายงานอัลฟ่าของ Cronbach (พร้อมตัวอย่าง)
วิธีรายงานผลการทดสอบที: พร้อมตัวอย่าง
วิธีรายงานผลลัพธ์ของ Chi Square: พร้อมตัวอย่าง
วิธีรายงานความสัมพันธ์ของเพียร์สัน: พร้อมตัวอย่าง
วิธีรายงานผลลัพธ์การถดถอย: พร้อมตัวอย่าง