ช่วงความเชื่อมั่นสำหรับผลต่างของค่าเฉลี่ย
บทความนี้จะอธิบายว่าช่วงความเชื่อมั่นสำหรับความแตกต่างในค่าเฉลี่ยทางสถิติคืออะไร และใช้เพื่ออะไร ดังนั้น คุณจะค้นพบวิธีการคำนวณช่วงความเชื่อมั่นสำหรับผลต่างของสองค่าเฉลี่ยและแบบฝึกหัดที่ได้รับการแก้ไขทีละขั้นตอน
ช่วงความเชื่อมั่นสำหรับผลต่างของค่าเฉลี่ยคืออะไร?
ช่วงความเชื่อมั่นสำหรับผลต่างของค่าเฉลี่ย คือช่วงเวลาที่ให้ค่าสูงสุดและค่าต่ำสุดซึ่งระหว่างนั้นค่าของผลต่างของค่าเฉลี่ยของประชากรทั้งสองจะอยู่ที่ระดับความเชื่อมั่นที่แน่นอน
ตัวอย่างเช่น หากช่วงความเชื่อมั่นสำหรับความแตกต่างในค่าเฉลี่ยของประชากรสองกลุ่มที่มีระดับความเชื่อมั่น 95% คือ (3.5) นั่นหมายความว่าความแตกต่างระหว่างค่าเฉลี่ยของประชากรทั้งสองจะอยู่ระหว่าง 3 ถึง 5 ด้วยความน่าจะเป็น 95 %
ดังนั้นในสถิติจึงใช้ช่วงความเชื่อมั่นสำหรับความแตกต่างในค่าเฉลี่ยเพื่อประมาณค่าสองค่าระหว่างที่ความแตกต่างระหว่างประชากรสองคนหมายถึงอยู่ ดังนั้น เมื่อใช้ข้อมูลจากสองตัวอย่าง จึงเป็นไปได้ที่จะประมาณความแตกต่างระหว่างค่าเฉลี่ยประชากรได้
สูตรช่วงความเชื่อมั่นสำหรับผลต่างของค่าเฉลี่ย
สูตรสำหรับช่วงความเชื่อมั่นสำหรับผลต่างในค่าเฉลี่ยขึ้นอยู่กับว่าทราบค่าความแปรปรวนของประชากรหรือไม่ และหากไม่ทราบ ค่าแปรปรวนของประชากรจะถือว่าเท่ากันหรือไม่ . จากนั้นเราจะดูว่าช่วงความเชื่อมั่นสำหรับผลต่างค่าเฉลี่ยคำนวณอย่างไรในแต่ละกรณี
การเบี่ยงเบนที่ทราบ
สูตรในการคำนวณช่วงความเชื่อมั่นสำหรับผลต่างในค่าเฉลี่ยเมื่อทราบความแปรปรวนของประชากรทั้งสอง ด้วยระดับความเชื่อมั่น 1-α มีดังนี้:
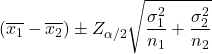
ทอง:
-

คือค่าเฉลี่ยของกลุ่มตัวอย่าง i
-

คือค่าเบี่ยงเบนมาตรฐานของประชากร i
-

คือค่าของการแจกแจงแบบปกติมาตรฐานที่มีความน่าจะเป็น α/2
-

คือขนาดตัวอย่าง i
กรณีนี้เป็นกรณีที่พบบ่อยที่สุด เนื่องจากโดยทั่วไปไม่ทราบค่าของความแปรปรวนของประชากร
ความแปรปรวนที่ไม่รู้จักและเท่ากัน
เมื่อไม่ทราบความแปรปรวนของประชากรทั้งสองแต่สามารถประมาณได้ว่าเท่ากัน สูตรในการคำนวณช่วงความเชื่อมั่นสำหรับผลต่างของค่าเฉลี่ย ด้วยระดับความเชื่อมั่น 1-α จะเป็นดังนี้:
![]()
ทอง:
-

คือค่าเฉลี่ยของกลุ่มตัวอย่าง i
-

คือค่าเบี่ยงเบนมาตรฐานรวม
-

คือค่าของการแจกแจง t ของนักเรียนที่มีดีกรีอิสระ n 1 + n 2 -2 ด้วยความน่าจะเป็น α/2
-

คือขนาดตัวอย่าง i
เนื่องจากในกรณีนี้ สันนิษฐานว่าความแปรปรวนของประชากรเท่ากัน จึงใช้ค่าเบี่ยงเบนมาตรฐานรวมในการคำนวณช่วงความเชื่อมั่น ซึ่งคำนวณโดยใช้สูตรต่อไปนี้

ทอง
![]()
คือค่าเบี่ยงเบนมาตรฐานของกลุ่มตัวอย่าง i
รูปแบบที่ไม่รู้จักและแตกต่างกัน
เมื่อไม่ทราบความแปรปรวนของประชากรทั้งสองและไม่สามารถถือว่าเท่ากันได้ สูตรในการคำนวณช่วงความเชื่อมั่นสำหรับผลต่างของค่าเฉลี่ย ด้วยระดับความเชื่อมั่น 1-α จะเป็นดังนี้:
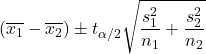
ทอง:
-

คือค่าเฉลี่ยของกลุ่มตัวอย่าง i
-
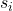
คือค่าเบี่ยงเบนมาตรฐานของกลุ่มตัวอย่าง i
-

คือค่าของการแจกแจง t ของนักเรียนที่มีความน่าจะเป็น α/2
-

คือขนาดตัวอย่าง i
ในกรณีนี้ องศาอิสระของการแจกแจง t ของนักเรียนคำนวณโดยใช้สูตรต่อไปนี้:

ทอง
![]()
คือค่าเบี่ยงเบนมาตรฐานของกลุ่มตัวอย่าง i
ตัวอย่างที่เป็นรูปธรรมของช่วงความเชื่อมั่นสำหรับผลต่างของค่าเฉลี่ย
หลังจากที่ได้เห็นคำจำกัดความของช่วงความเชื่อมั่นสำหรับผลต่างของค่าเฉลี่ยและสูตรที่แตกต่างกันแล้ว ตอนนี้เราจะเห็นตัวอย่างที่เป็นรูปธรรมเพื่อสรุปวิธีคำนวณช่วงความเชื่อมั่นสำหรับผลต่างของค่าเฉลี่ยทั้งสอง
- เราต้องการศึกษาผลของยาสูบต่อน้ำหนักแรกเกิดของเด็ก เมื่อต้องการทำเช่นนี้ จะมีการเปรียบเทียบสองตัวอย่าง: ตัวอย่างแรกประกอบด้วยเด็กที่มารดาไม่สูบบุหรี่ และตัวอย่างที่สองประกอบด้วยเด็กที่มารดาสูบบุหรี่ (พารามิเตอร์ตัวอย่างระบุไว้ด้านล่าง) คำนวณช่วงความเชื่อมั่นสำหรับผลต่างของค่าเฉลี่ยด้วยระดับความเชื่อมั่น 95%
- มารดาที่ไม่สูบบุหรี่:
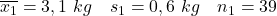
- มารดาที่สูบบุหรี่:
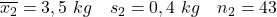
- มารดาที่ไม่สูบบุหรี่:
ในกรณีนี้ เราไม่ทราบค่าของความแปรปรวนของประชากร อย่างไรก็ตาม เราสามารถสรุปได้ว่าความแปรปรวนของประชากรนั้นเท่ากัน เนื่องจากเรากำลังเผชิญกับประชากรสองกลุ่มที่มีลักษณะคล้ายกันมาก ดังนั้น สูตรหาช่วงความเชื่อมั่นสำหรับผลต่างของค่าเฉลี่ยที่เราควรใช้คือ
![]()
ดังนั้นเราจึงคำนวณค่าเบี่ยงเบนมาตรฐานรวมจากค่าเบี่ยงเบนมาตรฐานของทั้งสองตัวอย่าง:
![Rendered by QuickLaTeX.com \begin{aligned}\displaystyle s_p&=\sqrt{\frac{(n_1-1)s_1^2+(n_2-1)s_2^2}{n_1+n_2-2}}\\[2ex]\displaystyle s_p&=\sqrt{\frac{(39-1)\cdot 0,6^2+(43-1)\cdot 0,4^2}{39+43-2}}\\[2ex]\displaystyle s_p&=0,50\end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-688958252e9838e7fddc2ddcb9061b01_l3.png)
ในทำนองเดียวกัน เราต้องหาค่าของการแจกแจง t ของนักเรียนที่ 80 องศาอิสระ ที่มีความน่าจะเป็น 2.5% ใน ตารางการกระจายความน่าจะเป็นของการแจกแจง t ของนักเรียน :
![]()
![Rendered by QuickLaTeX.com \begin{array}{c}t_{\alpha/2| n_1+n_2-2}= \ \color{orange}\bm{?}\\[4ex]t_{0,025|80}=1,990\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-5e4ea90fdc33c9a3d3dab0f1d9d29af0_l3.png)
สุดท้าย เราแทนที่ข้อมูลลงในสูตรช่วงความเชื่อมั่นเพื่อหาค่าความแตกต่างในค่าเฉลี่ยและทำการคำนวณ:
![]()
![]()
![]()
ช่วงความเชื่อมั่นสำหรับผลต่างของวิธีการของปัญหาจึงเป็นดังนี้:
![]()