Excel: คำนวณช่วงความเชื่อมั่นสำหรับสัมประสิทธิ์การถดถอย
ในแบบจำลองการถดถอยเชิง เส้น ค่าสัมประสิทธิ์การถดถอย บอกเราถึงการเปลี่ยนแปลงโดยเฉลี่ยใน ตัวแปรตอบสนอง ที่เกี่ยวข้องกับการเพิ่มขึ้นหนึ่งหน่วยในตัวแปรทำนาย
เราสามารถใช้สูตรต่อไปนี้เพื่อคำนวณช่วงความเชื่อมั่นสำหรับสัมประสิทธิ์การถดถอย:
ช่วงความเชื่อมั่นสำหรับ β 1 : b 1 ± t 1-α/2, n-2 * se(b 1 )
ทอง:
- b 1 = สัมประสิทธิ์การถดถอยที่แสดงในตารางการถดถอย
- t 1-∝/2, n-2 = ค่า t วิกฤตสำหรับระดับความเชื่อมั่น 1-∝ โดยมีดีกรีอิสระ n-2 โดยที่ n คือจำนวนการสังเกตทั้งหมดในชุดข้อมูลของเรา
- se(b 1 ) = ค่าคลาดเคลื่อนมาตรฐานของ b 1 ที่แสดงในตารางการถดถอย
ตัวอย่างต่อไปนี้แสดงวิธีการคำนวณช่วงความเชื่อมั่นสำหรับสัมประสิทธิ์การถดถอยใน Excel
ตัวอย่าง: ช่วงความเชื่อมั่นสำหรับค่าสัมประสิทธิ์การถดถอยใน Excel
สมมติว่าเราต้องการปรับโมเดลการถดถอยเชิงเส้นอย่างง่ายโดยใช้ ชั่วโมงที่ศึกษา เป็นตัวแปรทำนายและ คะแนนสอบ เป็นตัวแปรตอบกลับสำหรับนักเรียน 15 คนในชั้นเรียนหนึ่งๆ:
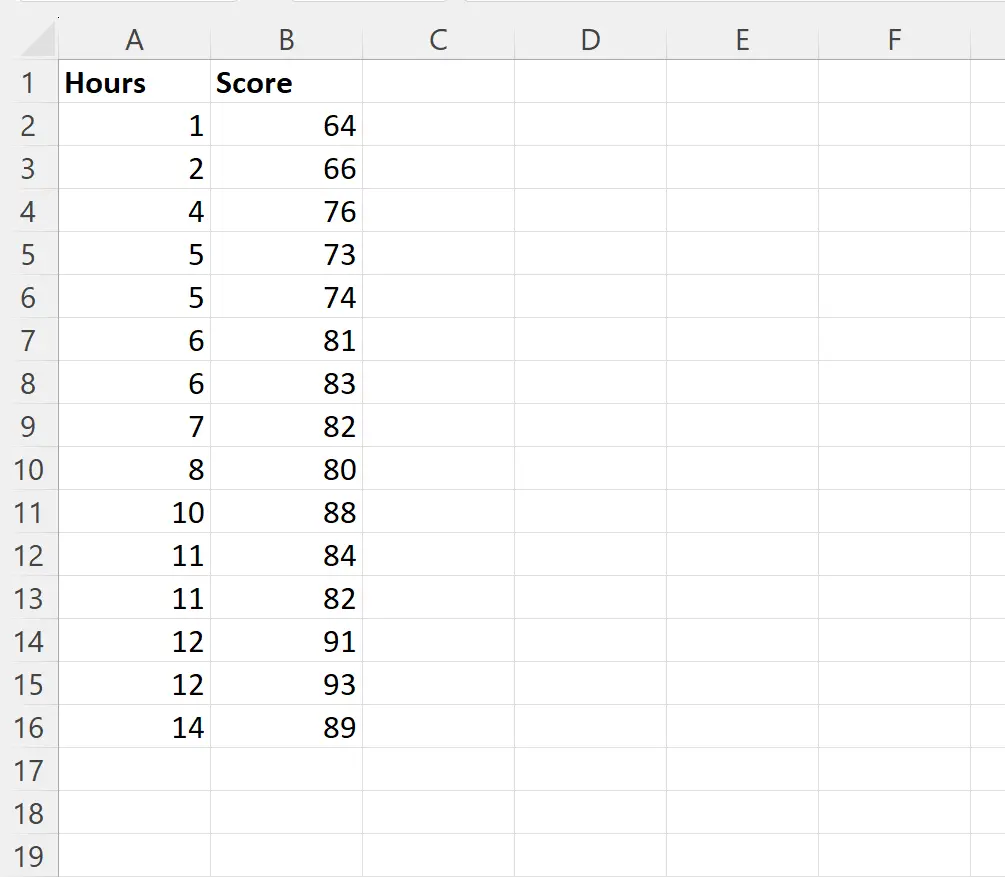
เราสามารถพิมพ์สูตรต่อไปนี้ในเซลล์ D2 เพื่อทำการถดถอยเชิงเส้นอย่างง่ายโดยใช้ค่าในคอลัมน์ ชั่วโมง เป็นตัวแปรทำนายและค่าในคอลัมน์ คะแนน เป็นตัวแปรตอบสนอง:
=LINEST( B2:B16 , A2:A16 , TRUE, TRUE)
โปรดทราบว่าอาร์กิวเมนต์ TRUE แรกจะบอก Excel ให้คำนวณจุดตัดของสมการการถดถอยตามปกติโดยไม่ต้องบังคับให้เป็นศูนย์
อาร์กิวเมนต์ TRUE ที่สองบอกให้ Excel สร้างสถิติการถดถอยเพิ่มเติมนอกเหนือจากค่าสัมประสิทธิ์
ภาพหน้าจอต่อไปนี้แสดงผลลัพธ์ของสูตรนี้ (เราอธิบายว่าค่าเอาต์พุตแต่ละค่าแสดงถึงอะไรในข้อความสีแดงด้านล่างผลลัพธ์):
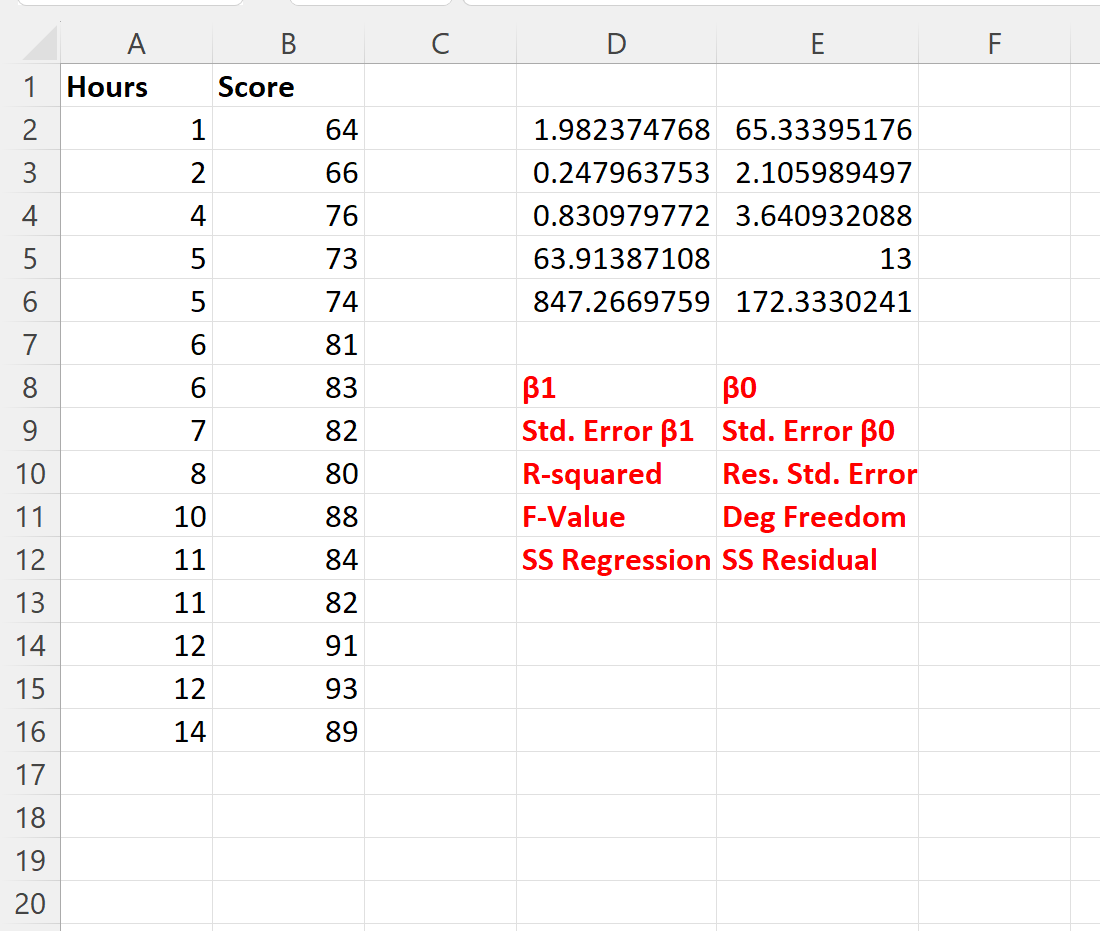
เมื่อใช้สัมประสิทธิ์การถดถอย เราสามารถเขียนสมการถดถอยที่ติดตั้งได้ดังนี้
คะแนน = 65.334 + 1.982*(ชั่วโมงเรียน)
โปรดทราบว่าค่าสัมประสิทธิ์การถดถอยสำหรับชั่วโมงคือ 1.982
สิ่งนี้บอกเราว่าการใช้เวลาเรียนเพิ่มเติมแต่ละชั่วโมงสัมพันธ์กับคะแนนสอบที่เพิ่มขึ้นโดยเฉลี่ย 1,982
ในการคำนวณช่วงความเชื่อมั่น 95% สำหรับสัมประสิทธิ์การถดถอย เราสามารถป้อนสูตรต่อไปนี้ในเซลล์ H2 และ H3:
- H2: = D2 – T.INV.2T(0.05, E5)*D3
- H3: = D2 + T.INV.2T(0.05, E5)*D3
ภาพหน้าจอต่อไปนี้แสดงวิธีใช้สูตรเหล่านี้ในทางปฏิบัติ:
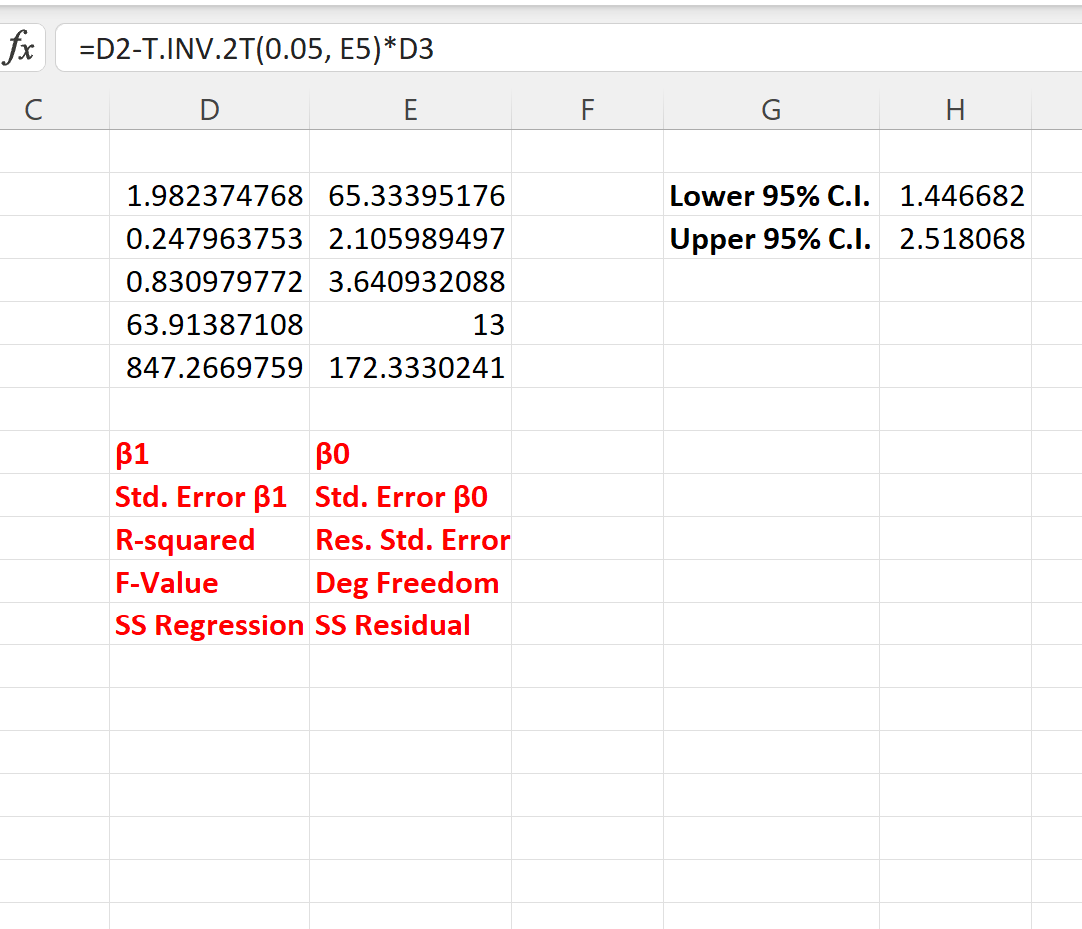
ช่วงความเชื่อมั่น 95% สำหรับสัมประสิทธิ์การถดถอยคือ [1.446, 2.518]
เนื่องจากช่วงความเชื่อมั่นนี้ ไม่มีค่า 0 เราจึงสามารถสรุปได้ว่ามีความสัมพันธ์ที่มีนัยสำคัญทางสถิติระหว่างชั่วโมงเรียนและเกรดการสอบ
นอกจากนี้เรายังสามารถยืนยันได้ว่าสิ่งนี้ถูกต้องโดยการคำนวณช่วงความเชื่อมั่น 95% สำหรับสัมประสิทธิ์การถดถอยด้วยตนเอง:
- CI 95% สำหรับ β 1 : b 1 ± t 1-α/2, n-2 * se(b 1 )
- CI 95% สำหรับ β 1 : 1.982 ± t 0.975, 15-2 * 0.248
- CI 95% สำหรับ β 1 : 1.982 ± 2.1604 * 0.248
- CI 95% สำหรับ β 1 : [1.446, 2.518]
ช่วงความเชื่อมั่น 95% สำหรับสัมประสิทธิ์การถดถอยคือ [1.446, 2.518]
แหล่งข้อมูลเพิ่มเติม
บทช่วยสอนต่อไปนี้อธิบายวิธีการทำงานทั่วไปอื่นๆ ใน Excel:
วิธีดำเนินการถดถอยเชิงเส้นอย่างง่ายใน Excel
วิธีการดำเนินการถดถอยเชิงเส้นหลายรายการใน Excel
วิธีการตีความค่า P ในเอาต์พุตการถดถอยใน Excel