ดัชนีจินี (หรือค่าสัมประสิทธิ์จินี)

บทความนี้จะอธิบายว่าดัชนี Gini หรือที่เรียกว่าสัมประสิทธิ์ Gini คืออะไร และใช้เพื่ออะไร นอกจากนี้ คุณจะพบกับแบบฝึกหัดที่แก้ไขได้เกี่ยวกับวิธีการค้นหาดัชนี Gini สุดท้าย คุณจะสามารถดูการตีความตัวชี้วัดทางสถิตินี้ และความสัมพันธ์ระหว่างดัชนี Gini และเส้นโค้ง Lorenz คืออะไร

ดัชนี Gini คืออะไร?

ดัชนี Gini หรือที่เรียกว่า สัมประสิทธิ์ Gini เป็นค่าทางสถิติที่ใช้ในการวัดความไม่เท่าเทียมกันของรายได้ของดินแดน กล่าวอีกนัยหนึ่ง ดัชนี Gini ระบุว่าอาณาเขตในการกระจายรายได้ระหว่างประชากรมีความเท่าเทียมกันเพียงใด

ดัชนี Gini เป็นตัวเลขระหว่าง 0 ถึง 1 หากดัชนี Gini เป็น 0 หมายความว่าการกระจายรายได้ในดินแดนนั้นมีความเท่าเทียมมากที่สุด (ความเสมอภาคที่สมบูรณ์แบบ) หรือกล่าวอีกนัยหนึ่งคือ ผู้อยู่อาศัยทุกคนมีรายได้เท่ากัน ในทางกลับกัน เมื่อค่าสัมประสิทธิ์จินีเป็น 1 สิ่งนี้จะสอดคล้องกับความไม่เท่าเทียมกันอย่างสมบูรณ์ กล่าวคือ บุคคลคนเดียวมีรายได้ทั้งหมดจากดินแดนนั้น และคนอื่นๆ ไม่ได้รับอะไรเลย

ดัชนี Gini ใช้เพื่อเปรียบเทียบสถานการณ์ทางเศรษฐกิจระหว่างประเทศต่างๆ ในโลก เนื่องจากทำให้สามารถเปรียบเทียบประเทศที่มีความเท่าเทียมมากที่สุด และในทางกลับกัน ประเทศที่ไม่เท่าเทียมกันมากที่สุดในแง่ของการกระจายรายได้

ดัชนี Gini ถูกคิดค้นโดยนักสถิติชื่อดัง Corrado Gini จึงเป็นที่มาของชื่อดัชนีนี้

วิธีการคำนวณดัชนี Gini

เมื่อพิจารณาจากคำจำกัดความของดัชนี Gini (หรือสัมประสิทธิ์ Gini) ต่อไปนี้คือวิธีคำนวณการวัดทางสถิตินี้

สูตรสำหรับดัชนี Gini (หรือค่าสัมประสิทธิ์ Gini) มีดังต่อไปนี้:

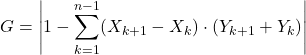
ทอง:

• 

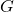
  คือดัชนีจินี่

• 

  คือสัดส่วนสะสมของประชากรแปรผัน

• 

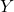
  คือสัดส่วนสะสมของตัวแปรรายได้

เพื่อให้คุณสามารถดูได้อย่างชัดเจนว่าดัชนี Gini ถูกกำหนดอย่างไร ตัวอย่างทีละขั้นตอนได้รับการแก้ไขด้านล่าง:

• คำนวณดัชนี Gini ของประชากรที่มีรายได้ตามตารางต่อไปนี้

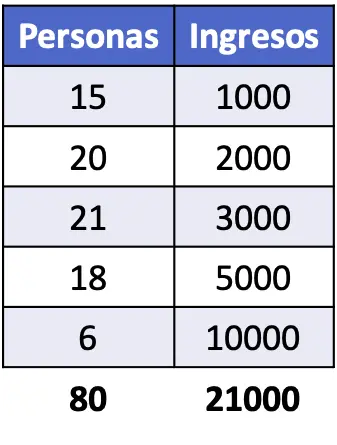
ในการจะหาค่าสัมประสิทธิ์จินี เราจำเป็นต้องกำหนดสัดส่วนของระดับรายได้แต่ละระดับและสัดส่วนสะสมด้วย นอกจากนี้ จะต้องคำนวณตามสูตรเพื่อค้นหาค่าของดัชนี Gini

กล่าวโดยสรุป ควรเพิ่มคอลัมน์ต่อไปนี้ลงในตารางข้อมูล:

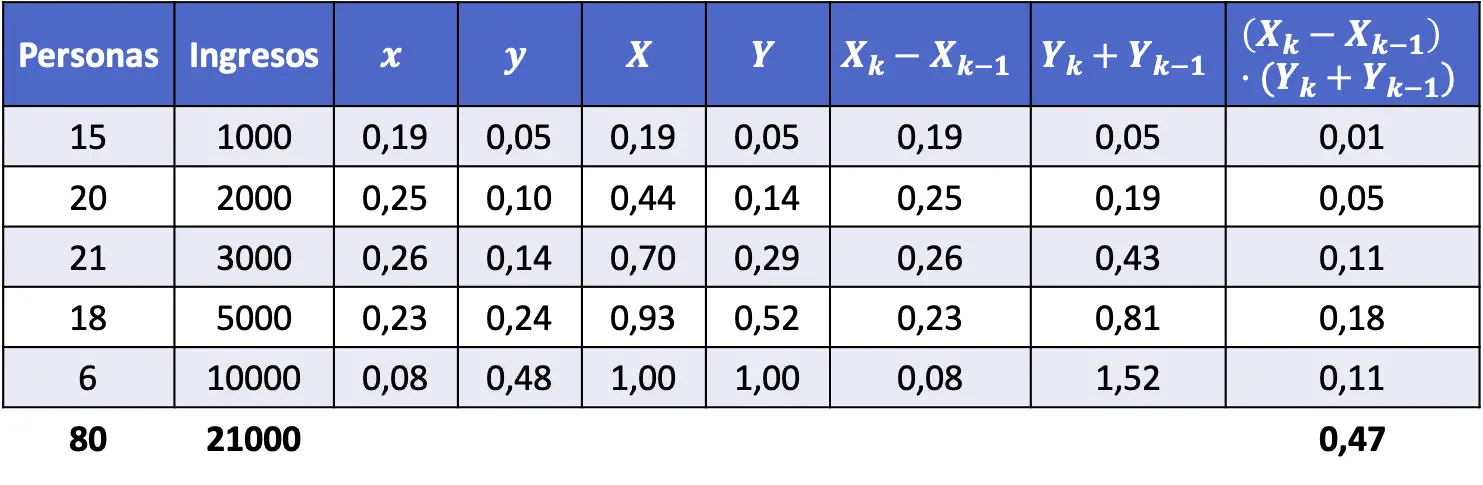
ตอนนี้เราใช้สูตรดัชนี Gini:

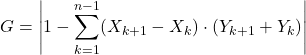
และสุดท้าย เราแทนที่ข้อมูลลงในนิพจน์พีชคณิตและคำนวณค่าสัมประสิทธิ์จินี:

ความสัมพันธ์ระหว่างดัชนี Gini และเส้นโค้ง Lorenz

ในส่วนนี้ เราจะดูว่าดัชนีจินีหรือที่เรียกว่าสัมประสิทธิ์จินีและเส้นโค้งลอเรนซ์มีความสัมพันธ์กันอย่างไร

เส้นโค้งลอเรนซ์ คือการแสดงภาพความไม่เท่าเทียมกันทางเศรษฐกิจของประชากรในดินแดนหนึ่งๆ ดังนั้น เส้นกราฟลอเรนซ์จึงแสดงให้เห็นความไม่เท่าเทียมกันทางเศรษฐกิจของประชากรด้วยสายตา

ในทางกลับกัน ดังที่เราได้เห็นไปแล้ว ดัชนี Gini เป็นค่าที่ใช้อธิบายความไม่เท่าเทียมกันของประชากรเป็นตัวเลข

ดัชนี Gini และเส้นโค้ง Lorenz จึงมีวัตถุประสงค์เดียวกัน คือ ทั้งสองค่าใช้เพื่อกำหนดความไม่เท่าเทียมกันทางเศรษฐกิจระหว่างผู้อยู่อาศัยในดินแดนหนึ่ง อย่างไรก็ตาม ดัชนี Gini จะประเมินความไม่เท่าเทียมกันของรายได้เป็นตัวเลข ในขณะที่กราฟ Lorenz วิเคราะห์ความไม่เท่าเทียมกันทางเศรษฐกิจในรูปแบบกราฟิก

นอกจากนี้ ดัชนี Gini สามารถคำนวณได้จากพื้นที่ที่ถูกจำกัดด้วยเส้นโค้ง Lorenz ตามสูตรต่อไปนี้:

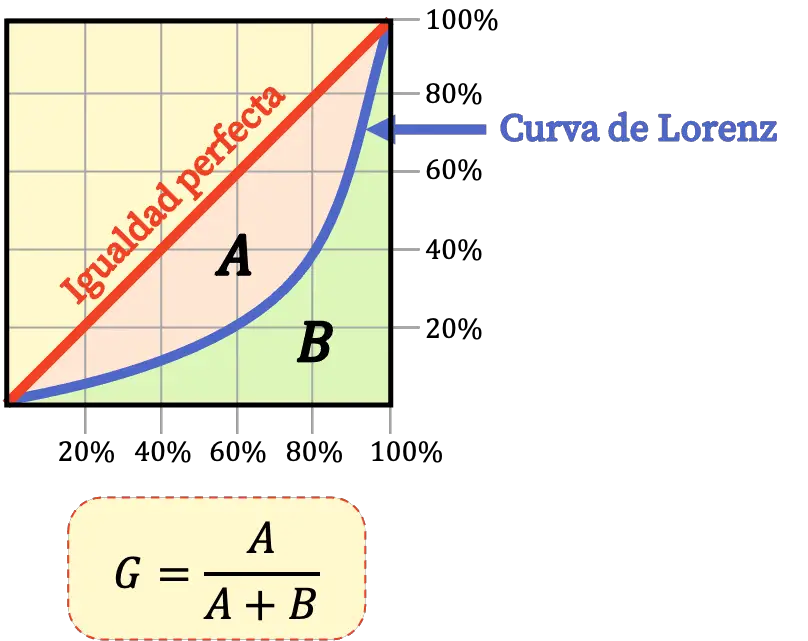
การตีความดัชนี Gini

ค่าของดัชนี Gini สามารถอยู่ในช่วงตั้งแต่ 0 ถึง 1 ทั้งคู่ ยิ่งค่าสัมประสิทธิ์ Gini มีค่าเข้าใกล้ 0 มากเท่าใด นั่นหมายความว่ามีความเท่าเทียมกันทางเศรษฐกิจมากขึ้นในดินแดนนั้น ในทางกลับกัน ยิ่งค่าดัชนี Gini สูงเท่าใด การกระจายรายได้ระหว่างผู้อยู่อาศัยในดินแดนหนึ่งก็จะยิ่งมีความไม่เท่าเทียมกันมากขึ้นเท่านั้น

ดังนั้นดัชนี Gini จะเท่ากับศูนย์ในสถานการณ์ที่เหมาะสมซึ่งผู้อยู่อาศัยทุกคนมีรายได้เท่ากันทุกประการ ในทางตรงกันข้าม ดัชนีจินีจะมีมูลค่า 1 เมื่อดินแดนนั้นมีความไม่เท่าเทียมกันโดยสิ้นเชิง กล่าวคือ ผู้อยู่อาศัยเพียงคนเดียวได้รับรายได้ทั้งหมด และผู้อยู่อาศัยที่เหลือไม่มีรายได้

ดังนั้น ประเทศที่มีความเท่าเทียมกันทางรายได้มากกว่าคือประเทศที่มีดัชนี Gini ต่ำกว่า และประเทศที่ไม่เท่าเทียมกันส่วนใหญ่ก็มีดัชนี Gini ที่สูงมาก

ดังที่เราได้เห็นแล้วว่าดัชนี Gini เชื่อมโยงกับเส้นโค้ง Lorenz ดังนั้น ยิ่งดัชนี Gini ต่ำ เส้นโค้ง Lorenz ก็จะเข้าใกล้เส้นที่มีความเท่าเทียมกันอย่างสมบูรณ์แบบมากขึ้นเท่านั้น แม้ว่าดัชนี Gini ยิ่งสูง เส้นโค้ง Gini ก็จะยิ่งมีความโค้งมากขึ้น ดังนั้น เส้นโค้งจะยิ่งอยู่ห่างจากเส้นที่แสดงถึงความเท่าเทียมกันที่สมบูรณ์แบบมากขึ้นเท่านั้น