ตัวอย่างค่าเบี่ยงเบนมาตรฐาน (หรือตัวอย่างค่าเบี่ยงเบนมาตรฐาน)

โดย ดร.เบนจามิน แอนเดอร์สัน สิงหาคม 3, 2023 สถิติ 0 ความคิดเห็น

บทความนี้จะอธิบายว่าค่าเบี่ยงเบนมาตรฐานตัวอย่างในสถิติคืออะไร ในทำนองเดียวกัน คุณจะได้เรียนรู้วิธีการคำนวณค่าเบี่ยงเบนมาตรฐานตัวอย่าง แบบฝึกหัดแก้ปัญหา และอะไรคือความแตกต่างระหว่างค่าเบี่ยงเบนมาตรฐานตัวอย่างกับค่าเบี่ยงเบนมาตรฐานประชากร สุดท้ายนี้ คุณสามารถคำนวณค่าเบี่ยงเบนมาตรฐานตัวอย่างใดๆ ได้ด้วยเครื่องคิดเลขออนไลน์

ค่าเบี่ยงเบนมาตรฐานตัวอย่างคืออะไร?

ค่าเบี่ยงเบนมาตรฐานตัวอย่าง (หรือ ค่าเบี่ยงเบนมาตรฐานตัวอย่าง ) คือการวัดการกระจายตัวที่บ่งบอกถึงความแปรปรวนของตัวอย่าง แม่นยำยิ่งขึ้น ค่าเบี่ยงเบนมาตรฐานของกลุ่มตัวอย่างจะเท่ากับรากที่สองของผลรวมของกำลังสองของส่วนเบี่ยงเบนหารด้วยขนาดตัวอย่างลบหนึ่ง

สัญลักษณ์สำหรับค่าเบี่ยงเบนมาตรฐานตัวอย่างคืออักษรตัวพิมพ์เล็ก s

ค่าเบี่ยงเบนมาตรฐานตัวอย่างบางครั้งเรียกว่าค่าเบี่ยงเบนมาตรฐานเสมือน (หรือค่าเบี่ยงเบนมาตรฐานเสมือน) เพื่อแยกความแตกต่างจากค่าเบี่ยงเบนมาตรฐานประชากร ด้านล่างนี้เราจะดูว่าค่าเบี่ยงเบนมาตรฐานตัวอย่างแตกต่างจากค่าเบี่ยงเบนมาตรฐานประชากรอย่างไร

ตัวอย่างสูตรส่วนเบี่ยงเบนมาตรฐาน

ค่าเบี่ยงเบนมาตรฐานของกลุ่มตัวอย่างเท่ากับรากที่สองของผลรวมของกำลังสองของส่วนเบี่ยงเบนของข้อมูลตัวอย่างหารด้วยขนาดตัวอย่างลบด้วยหนึ่ง ดังนั้น สูตรในการคำนวณค่าเบี่ยงเบนมาตรฐานตัวอย่าง คือ:

สูตรสำหรับค่าเบี่ยงเบนมาตรฐานตัวอย่างหรือค่าเบี่ยงเบนมาตรฐานตัวอย่าง.png

ทอง:

$s$

คือค่าเบี่ยงเบนมาตรฐานตัวอย่าง (หรือค่าเบี่ยงเบนมาตรฐานตัวอย่าง)
$x_i$

คือค่าข้อมูล

$i$

.
$n$

คือขนาดตัวอย่าง
$\overline{x}$

คือค่าเฉลี่ยตัวอย่าง

👉 คุณสามารถใช้เครื่องคิดเลขด้านล่างเพื่อคำนวณค่าเบี่ยงเบนมาตรฐานของตัวอย่างข้อมูลใดก็ได้

ตัวอย่างการคำนวณค่าเบี่ยงเบนมาตรฐานตัวอย่าง

ตอนนี้เรารู้คำจำกัดความของค่าเบี่ยงเบนมาตรฐานตัวอย่างแล้ว (หรือค่าเบี่ยงเบนมาตรฐานตัวอย่าง) และสูตรของมันคืออะไร เราจะแก้ตัวอย่างง่ายๆ เพื่อทำความเข้าใจวิธีการคำนวณให้เสร็จสิ้น

บริษัทรองเท้าแห่งหนึ่งกำลังดำเนินการวิจัยตลาดเพื่อตัดสินใจว่าจะเปิดตัวรองเท้ารุ่นใหม่หรือไม่ เนื่องจากมีหลายรุ่นและคุณเพียงต้องการวิเคราะห์เบื้องต้นอย่างรวดเร็ว คุณจึงตัดสินใจดูราคาตัวอย่างจากแบรนด์รองเท้าคู่แข่ง 5 อันดับแรกเท่านั้น (ราคาแสดงไว้ด้านล่าง) ค่าเบี่ยงเบนมาตรฐานของชุดข้อมูลนี้คืออะไร?

€98 €70 €125 €89 €75

ในการคำนวณค่าเบี่ยงเบนมาตรฐานของกลุ่มตัวอย่าง เราต้องคำนวณ ค่าเฉลี่ยของกลุ่มตัวอย่าง ก่อน:

$\overline{x}=\cfrac{98+70+125+89+75}{5}=91,4$

เมื่อคำนวณค่าเฉลี่ยตัวอย่างแล้ว เราจะใช้สูตรค่าเบี่ยงเบนมาตรฐานตัวอย่าง:

$\displaystyle s=\sqrt{\frac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{x}\right)^2}{n-1}}$

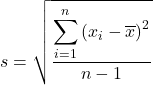
เราแทนที่ข้อมูลตัวอย่างลงในสูตร:

$\displaystyle s=\sqrt{\frac{\displaystyle (98-91,4)^2+(70-91,4)^2+(125-91,4)^2+(89-91,4)^2+(75-91,4)^2}{5-1}}$

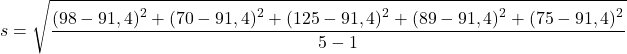
ดังนั้น สิ่งที่เหลืออยู่คือการแก้ปัญหาการดำเนินการเพื่อคำนวณค่าเบี่ยงเบนมาตรฐานของกลุ่มตัวอย่าง:

$\begin{aligned}\displaystyle s&=\sqrt{\frac{6,6^2+(-21,4)^2+33,6^2+(-2,4)^2+(-16,4)^2}{4}}\\[2ex]\displaystyle s&=\sqrt{\frac{43,56+457,96+1128,96+5,76+268,96}{4}}\\[2ex]s&=\sqrt{\frac{1905,2}{4}}\\[2ex]s&=\sqrt{476,3}\\[2ex]s&=21,82 \end{aligned}$

ดังนั้นความแตกต่างในการสุ่มตัวอย่างของกลุ่มตัวอย่างที่วิเคราะห์คือ €21.82

➤ ดู: รูปแบบการสุ่มตัวอย่าง

ตัวอย่างค่าเบี่ยงเบนมาตรฐานและค่าเบี่ยงเบนมาตรฐานประชากร

ต่อไป เราจะดูว่าอะไรคือความแตกต่างระหว่างค่าเบี่ยงเบนมาตรฐานตัวอย่างกับค่าเบี่ยงเบนมาตรฐานประชากร เพราะนี่คือแนวคิดทางสถิติที่เกี่ยวข้องสองประการที่เราจำเป็นต้องทำให้ชัดเจน

ในสถิติ ค่า เบี่ยงเบนมาตรฐานของประชากร คือค่าเบี่ยงเบนมาตรฐานที่ได้เมื่อคำนวณด้วยองค์ประกอบทั้งหมดของประชากร แม้ว่า ค่าเบี่ยงเบนมาตรฐาน จะเป็นค่าเบี่ยงเบนมาตรฐานที่ได้จากการคำนวณโดยใช้ข้อมูลจากประชากรเพียงตัวอย่างเดียว .

ในทางคณิตศาสตร์ ความแตกต่างระหว่างค่าเบี่ยงเบนมาตรฐานของกลุ่มตัวอย่างและค่าเบี่ยงเบนมาตรฐานของประชากร คือตัวหารของสูตรที่ใช้ในการคำนวณ ในการคำนวณค่าเบี่ยงเบนมาตรฐานของกลุ่มตัวอย่าง จะต้องหารด้วย n-1 ในขณะที่ค่าเบี่ยงเบนมาตรฐานของประชากรคำนวณโดยการหารด้วย n

นอกจากนี้ เพื่อแยกความแตกต่างระหว่างค่าเบี่ยงเบนมาตรฐานของกลุ่มตัวอย่างจากค่าเบี่ยงเบนมาตรฐานของประชากร จะแสดงด้วยสัญลักษณ์ที่แตกต่างกัน สัญลักษณ์ของค่าเบี่ยงเบนมาตรฐานของกลุ่มตัวอย่างคือตัวอักษร s ในขณะที่สัญลักษณ์ของค่าเบี่ยงเบนมาตรฐานของประชากรคือตัวอักษรกรีก σ

โดยทั่วไป องค์ประกอบบางอย่างของประชากรยังไม่ทราบ ดังนั้นการศึกษาทางสถิติจึงดำเนินการกับกลุ่มตัวอย่างประชากร ดังนั้น ค่าเบี่ยงเบนมาตรฐานของกลุ่มตัวอย่างจึงถูกนำมาใช้ในการประมาณค่าจุดของค่าเบี่ยงเบนมาตรฐานของประชากรทั้งหมด

➤ ดู: ค่าเบี่ยงเบนมาตรฐานของประชากร

ตัวอย่างเครื่องคิดเลขค่าเบี่ยงเบนมาตรฐาน

ป้อนข้อมูลของกลุ่มตัวอย่างลงในเครื่องคิดเลขออนไลน์ต่อไปนี้เพื่อคำนวณค่าเบี่ยงเบนมาตรฐานของกลุ่มตัวอย่าง (หรือส่วนเบี่ยงเบนมาตรฐานของกลุ่มตัวอย่าง) ข้อมูลต้องคั่นด้วยช่องว่างและป้อนโดยใช้จุดเป็นตัวคั่นทศนิยม

เกี่ยวกับผู้แต่ง

ดร.เบนจามิน แอนเดอร์สัน

สวัสดี ฉันชื่อเบนจามิน ศาสตราจารย์สถิติเกษียณอายุแล้ว และผันตัวมาเป็นครูสอนสถิติโดยเฉพาะ ด้วยประสบการณ์และความเชี่ยวชาญที่กว้างขวางในสาขาสถิติ ฉันกระตือรือร้นที่จะแบ่งปันความรู้ของฉันเพื่อเสริมศักยภาพนักเรียนผ่าน Statorials. รู้เพิ่มเติม