ตัวแปรสุ่มคืออะไร?
ตัวแปร สุ่ม ซึ่งโดยทั่วไปจะแสดงแทน X เป็นตัวแปรที่มีค่าที่เป็นไปได้คือผลลัพธ์ของกระบวนการสุ่ม
ตัวแปรสุ่มมีสองประเภท: แบบแยก และ แบบต่อเนื่อง
ตัวแปรสุ่มแบบไม่ต่อเนื่อง
ตัวแปรสุ่มแบบไม่ต่อเนื่อง คือตัวแปรที่สามารถนับเฉพาะค่าที่แตกต่าง เช่น 0, 1, 2, 3, 4, 5…100, 1 ล้าน เป็นต้น นี่คือตัวอย่างบางส่วนของตัวแปรสุ่มแบบไม่ต่อเนื่อง:
- จำนวนครั้งที่เหรียญลงก้อยหลังจากถูกโยนครบ 20 ครั้ง
- จำนวนครั้งที่ลูกเต๋าตกลงบนหมายเลข 4 หลังจากทอยครบ 100 ครั้ง
- จำนวนวิดเจ็ตที่ชำรุดในกล่อง 50 วิดเจ็ต
การแจกแจงความน่าจะเป็น สำหรับตัวแปรสุ่มแบบไม่ต่อเนื่องจะบอกเราถึงความน่าจะเป็นที่ตัวแปรสุ่มจะใช้กับค่าบางค่า
ตัวอย่างเช่น สมมติว่าเราทอยลูกเต๋าหนึ่งครั้ง หากเราให้ X แสดงถึงความน่าจะเป็นที่การตายจะตรงกับจำนวนที่กำหนด การแจกแจงความน่าจะเป็นสามารถเขียนได้ดังนี้:
- ป(X=1): 1/6
- ป(X=2): 1/6
- ป(X=3): 1/6
- ป(X=4): 1/6
- ป(X=5): 1/6
- ป(X=6): 1/6
บันทึก:
เพื่อให้การแจกแจงความน่าจะเป็นถูกต้อง ต้องเป็นไปตามเกณฑ์สองข้อต่อไปนี้:
1. ความน่าจะเป็นของแต่ละผลลัพธ์จะต้องอยู่ระหว่าง 0 ถึง 1
2. ผลรวมของความน่าจะเป็นทั้งหมดต้องรวมกันเป็น 1
โปรดทราบว่าการกระจายความน่าจะเป็นสำหรับลูกกลิ้งแม่พิมพ์เป็นไปตามเกณฑ์ทั้งสองข้อนี้:
1. ความน่าจะเป็นของแต่ละผลลัพธ์อยู่ระหว่าง 0 ถึง 1
2. ผลรวมของความน่าจะเป็นทั้งหมดรวมกันได้ 1
เราสามารถใช้ฮิสโตแกรมเพื่อแสดงภาพการแจกแจงความน่าจะเป็น:
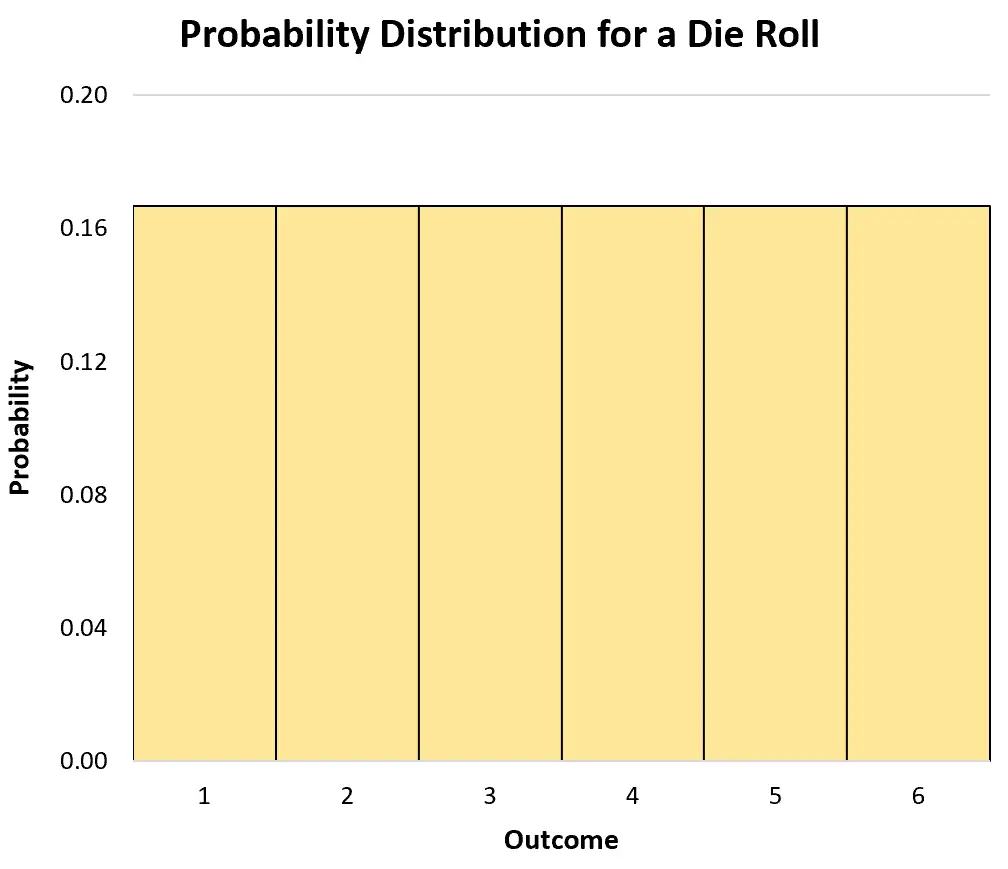
การแจกแจงความน่าจะเป็นสะสม สำหรับตัวแปรสุ่มแบบไม่ต่อเนื่องจะบอกเราถึงความน่าจะเป็นที่ตัวแปรจะได้รับค่า ที่เท่ากับหรือน้อยกว่า ค่าที่กำหนด
ตัวอย่างเช่น การแจกแจงความน่าจะเป็นสะสมสำหรับทอยลูกเต๋าจะมีลักษณะดังนี้:
- ป(X≤1): 1/6
- ป(X≤2): 2/6
- พี(X≤3): 3/6
- ป(X≤4): 4/6
- ป(X≤5): 5/6
- ป(X≤6): 6/6
โอกาสที่ความตายจะตกลงไปที่หนึ่งหรือน้อยกว่าคือเพียง 1/6 เนื่องจากไม่สามารถตกลงไปที่จำนวนที่น้อยกว่าหนึ่งได้
ความน่าจะเป็นที่มันจะตกบนสองหรือน้อยกว่าคือ P(X=1) + P(X=2) = 1/6 + 1/6 = 2/6
ในทำนองเดียวกัน ความน่าจะเป็นที่มันจะตกบนสามหรือน้อยกว่าคือ P(X=1) + P(X=2) + P(X=3) = 1/6 + 1/6 + 1/6 = 3/6 และ เร็วๆ นี้.
นอกจากนี้เรายังสามารถใช้ฮิสโตแกรมเพื่อแสดงภาพการแจกแจงความน่าจะเป็นสะสม:
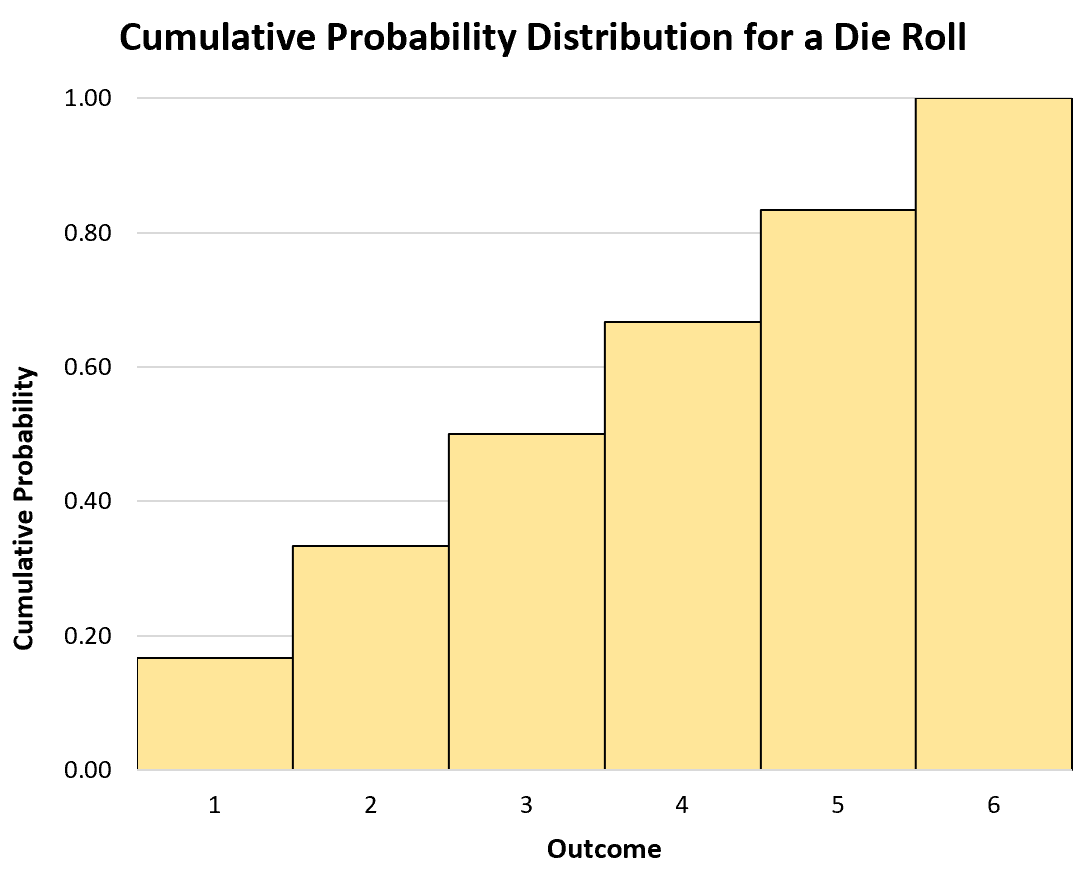
ตัวแปรสุ่มต่อเนื่อง
ตัวแปรสุ่มต่อเนื่อง คือตัวแปรที่สามารถรับค่าที่เป็นไปได้มากมายอย่างไม่สิ้นสุด นี่คือตัวอย่างบางส่วนของตัวแปรสุ่มแบบต่อเนื่อง:
- น้ำหนักของสัตว์
- ความสูงของบุคคล
- เวลาที่จำเป็นในการวิ่งมาราธอน
ตัวอย่างเช่น ความสูงของบุคคลอาจเป็น 60.2 นิ้ว, 65.2344 นิ้ว, 70.431222 นิ้ว เป็นต้น มีค่าขนาดที่เป็นไปได้จำนวนอนันต์
กฎทั่วไป:
หากคุณสามารถ นับ จำนวนผลลัพธ์ได้ แสดงว่าคุณกำลังทำงานกับตัวแปรสุ่มแบบแยกส่วน เช่น การนับจำนวนครั้งที่เหรียญขึ้นหัว
แต่หากคุณสามารถ วัด ผลลัพธ์ได้ คุณกำลังทำงานกับตัวแปรสุ่มอย่างต่อเนื่อง เช่น การวัดส่วนสูง น้ำหนัก เวลา ฯลฯ
การแจกแจงความน่าจะเป็น สำหรับตัวแปรสุ่มแบบต่อเนื่องจะบอกเราถึงความน่าจะเป็นที่ตัวแปรสุ่มจะใช้กับค่าบางค่า
อย่างไรก็ตาม ไม่เหมือนกับการแจกแจงความน่าจะเป็นสำหรับตัวแปรสุ่มแบบแยกตรง การแจกแจงความน่าจะเป็นสำหรับตัวแปรสุ่มแบบต่อเนื่องสามารถใช้เพื่อบอกเราถึงความน่าจะเป็นที่ตัวแปรจะใช้กับ ช่วง ของค่าต่างๆ เท่านั้น
ตัวอย่างเช่น สมมติว่าเราต้องการทราบความน่าจะเป็นที่แฮมเบอร์เกอร์จากร้านอาหารแห่งหนึ่งจะมีน้ำหนัก 1/4 ปอนด์ (0.25 ปอนด์) เนื่องจาก น้ำหนัก เป็นตัวแปรต่อเนื่อง จึงสามารถรับค่าจำนวนอนันต์ได้
ตัวอย่างเช่น แฮมเบอร์เกอร์หนึ่งชิ้นอาจมีน้ำหนักจริง 0.250001 ปอนด์ หรือ 0.24 ปอนด์ หรือ 0.2488 ปอนด์ ความน่าจะเป็นที่แฮมเบอร์เกอร์หนึ่งชิ้นจะมีน้ำหนัก 0.25 ปอนด์พอดีนั้นเป็นศูนย์
ดังนั้นเราจึงใช้เพียงการแจกแจงความน่าจะเป็นเพื่อบอกความน่าจะเป็นที่แฮมเบอร์เกอร์มีน้ำหนักน้อยกว่า 0.25 ปอนด์ มากกว่า 0.25 ปอนด์ หรืออยู่ระหว่างช่วงที่กำหนด (เช่น ระหว่าง 0.23 ปอนด์ถึง 0.27 ปอนด์)
แหล่งข้อมูลเพิ่มเติม
บทช่วยสอนต่อไปนี้ให้ข้อมูลเพิ่มเติมเกี่ยวกับตัวแปรสุ่ม: