วิธีการวาดเส้นโค้ง roc ใน python (ทีละขั้นตอน)
การถดถอยแบบลอจิสติก เป็นวิธีการทางสถิติที่เราใช้เพื่อปรับให้เหมาะสมกับแบบจำลองการถดถอยเมื่อตัวแปรตอบสนองเป็นไบนารี เพื่อประเมินว่าแบบจำลองการถดถอยโลจิสติกเหมาะสมกับชุดข้อมูลได้ดีเพียงใด เราสามารถดูตัวชี้วัดสองตัวต่อไปนี้:
- ความไว: ความน่าจะเป็นที่แบบจำลองคาดการณ์ผลลัพธ์ที่เป็นบวกสำหรับการสังเกต เมื่อผลลัพธ์เป็นบวกจริงๆ สิ่งนี้เรียกอีกอย่างว่า “อัตราบวกที่แท้จริง”
- ความจำเพาะ: ความน่าจะเป็นที่แบบจำลองทำนายผลลัพธ์ที่เป็นลบสำหรับการสังเกต เมื่อผลลัพธ์เป็นลบจริงๆ สิ่งนี้เรียกอีกอย่างว่า “อัตราติดลบที่แท้จริง”
วิธีหนึ่งในการแสดงภาพการวัดทั้งสองนี้คือการสร้าง เส้นโค้ง ROC ซึ่งย่อมาจากเส้นโค้ง “ลักษณะการทำงานของตัวรับ” นี่คือกราฟที่แสดงความไวและความเฉพาะเจาะจงของแบบจำลองการถดถอยลอจิสติก
ตัวอย่างทีละขั้นตอนต่อไปนี้แสดงวิธีสร้างและตีความเส้นโค้ง ROC ใน Python
ขั้นตอนที่ 1: นำเข้าแพ็คเกจที่จำเป็น
ขั้นแรก เราจะนำเข้าแพ็คเกจที่จำเป็นเพื่อทำการถดถอยโลจิสติกใน Python:
import pandas as pd import numpy as np from sklearn. model_selection import train_test_split from sklearn. linear_model import LogisticRegression from sklearn import metrics import matplotlib. pyplot as plt
ขั้นตอนที่ 2: ติดตั้งแบบจำลองการถดถอยโลจิสติก
ต่อไป เราจะนำเข้าชุดข้อมูลและปรับแบบจำลองการถดถอยโลจิสติกให้เหมาะสม:
#import dataset from CSV file on Github
url = "https://raw.githubusercontent.com/Statorials/Python-Guides/main/default.csv"
data = pd. read_csv (url)
#define the predictor variables and the response variable
X = data[[' student ',' balance ',' income ']]
y = data[' default ']
#split the dataset into training (70%) and testing (30%) sets
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.3,random_state=0)
#instantiate the model
log_regression = LogisticRegression()
#fit the model using the training data
log_regression. fit (X_train,y_train)
ขั้นตอนที่ 3: วาดเส้นโค้ง ROC
ต่อไป เราจะคำนวณอัตราบวกจริงและอัตราบวกลวง และสร้างเส้นโค้ง ROC โดยใช้แพ็คเกจการแสดงข้อมูล Matplotlib:
#define metrics
y_pred_proba = log_regression. predict_proba (X_test)[::,1]
fpr, tpr, _ = metrics. roc_curve (y_test, y_pred_proba)
#create ROC curve
plt. plot (fpr,tpr)
plt. ylabel (' True Positive Rate ')
plt. xlabel (' False Positive Rate ')
plt. show ()
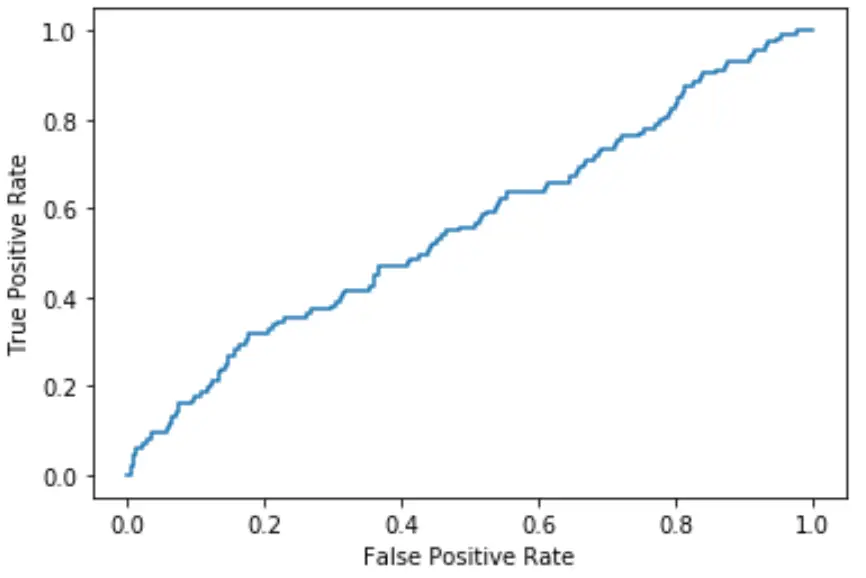
ยิ่งเส้นโค้งพอดีกับมุมซ้ายบนของพล็อตมากเท่าไร โมเดลก็ยิ่งสามารถจำแนกข้อมูลเป็นหมวดหมู่ได้ดีขึ้นเท่านั้น
ดังที่เราเห็นจากกราฟด้านบน โมเดลการถดถอยโลจิสติกนี้ทำงานได้ค่อนข้างแย่ในการจัดเรียงข้อมูลเป็นหมวดหมู่
ในการหาปริมาณ เราสามารถคำนวณ AUC ซึ่งเป็นพื้นที่ใต้เส้นโค้ง ซึ่งจะบอกเราว่าพล็อตอยู่ใต้เส้นโค้งเป็นจำนวนเท่าใด
ยิ่ง AUC ใกล้ 1 มากเท่าใด โมเดลก็ยิ่งดีเท่านั้น โมเดลที่มี AUC เท่ากับ 0.5 ไม่ได้ดีไปกว่าโมเดลที่มีการจำแนกแบบสุ่ม
ขั้นตอนที่ 4: คำนวณ AUC
เราสามารถใช้โค้ดต่อไปนี้เพื่อคำนวณ AUC ของโมเดลและแสดงไว้ที่มุมขวาล่างของพล็อต ROC:
#define metrics
y_pred_proba = log_regression. predict_proba (X_test)[::,1]
fpr, tpr, _ = metrics. roc_curve (y_test, y_pred_proba)
auc = metrics. roc_auc_score (y_test, y_pred_proba)
#create ROC curve
plt. plot (fpr,tpr,label=" AUC= "+str(auc))
plt. ylabel (' True Positive Rate ')
plt. xlabel (' False Positive Rate ')
plt. legend (loc=4)
plt. show ()
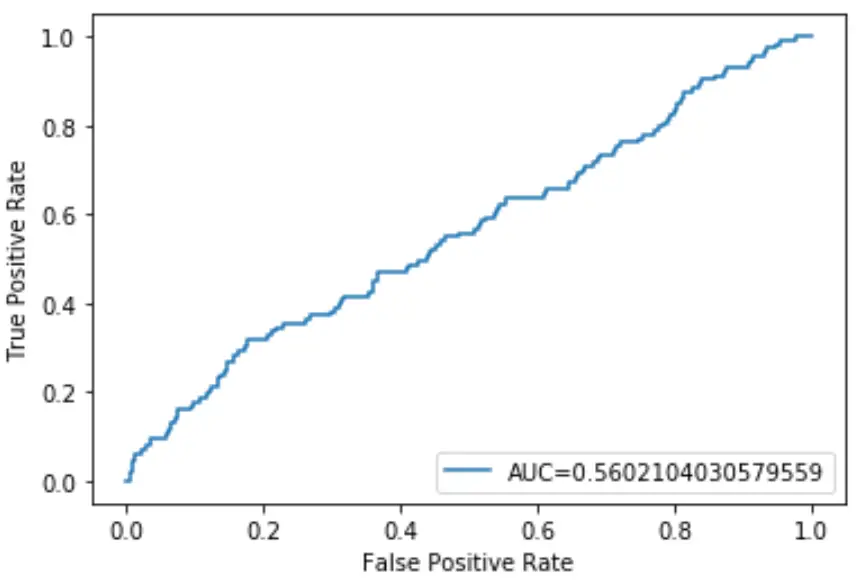
AUC ของแบบจำลองการถดถอยโลจิสติกนี้กลายเป็น 0.5602 เนื่องจากตัวเลขนี้ปิดอยู่ที่ 0.5 นี่เป็นการยืนยันว่าแบบจำลองทำหน้าที่จำแนกข้อมูลได้ไม่ดี
ที่เกี่ยวข้อง: วิธีพล็อตเส้นโค้ง ROC หลายรายการใน Python