ทฤษฎีบทของเชบีเชฟ

โดย ดร.เบนจามิน แอนเดอร์สัน สิงหาคม 5, 2023 ความน่าจะเป็น 0 ความคิดเห็น

บทความนี้จะอธิบายว่าทฤษฎีบทของเชบีเชฟคืออะไร ที่นี่คุณจะได้พบกับสูตรทฤษฎีบท Chebyshev แบบฝึกหัดแก้โจทย์ และนอกจากนี้ เครื่องคำนวณทฤษฎีบท Chebyshev ออนไลน์ ท้ายที่สุด มันแสดงให้เห็นความแตกต่างระหว่างทฤษฎีบทของเชบีเชฟกับกฎเชิงประจักษ์

ทฤษฎีบทของเชบีเชฟคืออะไร?

ทฤษฎีบทของเชบีเชฟ หรือที่รู้จักในชื่อ อสมการของเชบีเชฟ เป็นกฎทางสถิติที่ใช้ในการคำนวณความน่าจะเป็นที่ค่าของตัวแปรสุ่มจะอยู่ในระยะที่กำหนดจากค่าเฉลี่ย

กล่าวอีกนัยหนึ่ง ในทางสถิติ ทฤษฎีบทของเชบีเชฟใช้เพื่อกำหนดความน่าจะเป็นที่ค่าจะอยู่ภายในช่วงความเชื่อมั่น

นอกจากนี้ ทฤษฎีบทของเชบีเชฟยังใช้ในการพิสูจน์ทฤษฎีบททางสถิติอื่นๆ เช่น กฎของจำนวนมาก

แม้ว่าทฤษฎีบทของ Chebyshev ได้รับการคิดค้นครั้งแรกโดยชาวฝรั่งเศส Irénée-Jules Bienaymé แต่ทฤษฎีบทนี้ได้รับการตั้งชื่อเช่นนี้เนื่องจากทฤษฎีบทนี้มีต้นกำเนิดโดย Pafnuty Chebushev ชาวรัสเซียในปี พ.ศ. 2410

สูตรทฤษฎีบทของเชบีเชฟ

ทฤษฎีบทของเชบีเชฟกล่าวว่าความน่าจะเป็นที่ค่าจะเท่ากับ k ส่วนเบี่ยงเบนมาตรฐานจากค่าเฉลี่ย มากกว่าหรือเท่ากับ 1 ลบอัตราส่วนของหนึ่งหารด้วย k กำลังสอง

ดังนั้น สูตรสำหรับทฤษฎีบทของเชบีเชฟ จึงเป็นดังนี้:

$\displaystyle P(\mu-k\sigma\leq X \leq \mu+k\sigma)\geq 1 -\frac{1}{k^2}$

ทอง

$X$

คือค่าของตัวแปรสุ่ม

$\mu$

ค่าเฉลี่ยเลขคณิต ของตัวแปร

$\sigma$

ส่วนเบี่ยงเบนมาตรฐาน และ

$k$

จำนวนค่าเบี่ยงเบนมาตรฐานจากค่าเฉลี่ยที่จะคำนวณความน่าจะเป็น

โปรดทราบว่าสูตรนี้สามารถใช้ได้ก็ต่อเมื่อจำนวนส่วนเบี่ยงเบนมาตรฐานที่ใช้คำนวณมากกว่า 1 หรืออีกนัยหนึ่งคือ ถ้า k มากกว่า 1

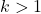$k>1″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”41″ style=”vertical-align: -2px;”></p> </p> <p> 👉 <u style=$ คุณสามารถใช้เครื่องคิดเลขทฤษฎีบทเชบีเชฟออนไลน์ด้านล่างเพื่อคำนวณความน่าจะเป็น

ตัวอย่างทฤษฎีบทของเชบีเชฟ

เมื่อเราได้เห็นคำจำกัดความของทฤษฎีบทของเชบีเชฟและสูตรของมันแล้ว ต่อไปนี้คือตัวอย่างที่ได้รับการแก้ไขแล้วของทฤษฎีบททางสถิตินี้เพื่อให้เข้าใจแนวคิดได้ดีขึ้น

หากคะแนนที่ได้รับในสถิติหลักสูตรของมหาวิทยาลัยถูกกำหนดโดยการแจกแจงที่มีค่าเฉลี่ย 65 และส่วนเบี่ยงเบนมาตรฐานคือ 10 นักเรียนจะได้เกรดระหว่าง 50 ถึง 80 เปอร์เซ็นต์กี่เปอร์เซ็นต์

เพื่อแก้ปัญหานี้ เราจำเป็นต้องใช้สูตรทฤษฎีบทของเชบีเชฟ อย่างไรก็ตาม อันดับแรกเราต้องกำหนดก่อนว่าค่าเบี่ยงเบนมาตรฐานของค่า 50 และ 80 นั้นมาจากค่าเฉลี่ยของตัวแปรเป็นจำนวนเท่าใด เมื่อต้องการทำเช่นนี้ เราเพียงแค่ต้องทำการคำนวณต่อไปนี้:

$k=\cfrac{\text{valor}-\text{media}}{\text{desviaci\'on t\'ipica}}$

$k=\cfrac{50-65}{10}=-1,5$

$k=\cfrac{80-65}{10}=1,5$

ดังนั้นค่า 50 และ 80 จึงสอดคล้องกับค่าเบี่ยงเบนมาตรฐาน 1.5 จากค่าเฉลี่ยล่างและบนตามลำดับ ดังนั้นเราจึงใช้สูตรทฤษฎีบทของเชบีเชวากับ k=1.5:

$\displaystyle P(\mu-k\sigma\leq X \leq \mu+k\sigma)\leq 1 -\frac{1}{k^2}$

$\displaystyle P(\mu-1,5\sigma\leq X \leq \mu+1,5\sigma)\leq 1 -\frac{1}{1,5^2}$

$\displaystyle P(50\leq X \leq 80)\leq 0,5556$

ดังนั้น นักเรียนอย่างน้อย 55.56% ได้เกรดระหว่าง 50 ถึง 80

เครื่องคำนวณทฤษฎีบทของ Chebyshev

ป้อนจำนวนส่วนเบี่ยงเบนมาตรฐานระหว่างค่าที่เป็นปัญหาและค่าเฉลี่ย (k) จากนั้นคลิก “คำนวณ” เครื่องคิดเลขจะคืนค่าความน่าจะเป็นขั้นต่ำของช่วงความเชื่อมั่น

คุณต้องป้อนจำนวนส่วนเบี่ยงเบนมาตรฐานโดยใช้จุดเป็นตัวคั่นทศนิยม

ทฤษฎีบทของเชบีเชฟและกฎทั่วไป

แนวคิดสองประการที่เกี่ยวข้องกันอย่างใกล้ชิดในสถิติคือ ทฤษฎีบทของเชบีเชฟและกฎเชิงประจักษ์ เนื่องจากทั้งสองแนวคิดใช้ในการคำนวณความน่าจะเป็นของช่วงความเชื่อมั่น

ความแตกต่างระหว่างทฤษฎีบทของเชบีเชฟและกฎเชิงประจักษ์ คือ ทฤษฎีบทของเชบีเชฟสามารถใช้กับการแจกแจงแบบใดก็ได้ ในขณะที่กฎเชิงประจักษ์ใช้ได้เฉพาะกับการแจกแจงแบบปกติเท่านั้น

การใช้ทฤษฎีบทของเชบีเชฟจึงกว้างกว่า แต่กฎเชิงประจักษ์ให้ผลลัพธ์ที่แม่นยำยิ่งขึ้นสำหรับการแจกแจงแบบปกติ

คลิกที่นี่เพื่อดูว่ากฎทั่วไปคืออะไร:

➤ ดู: กฎทั่วไป

เกี่ยวกับผู้แต่ง

ดร.เบนจามิน แอนเดอร์สัน

สวัสดี ฉันชื่อเบนจามิน ศาสตราจารย์สถิติเกษียณอายุแล้ว และผันตัวมาเป็นครูสอนสถิติโดยเฉพาะ ด้วยประสบการณ์และความเชี่ยวชาญที่กว้างขวางในสาขาสถิติ ฉันกระตือรือร้นที่จะแบ่งปันความรู้ของฉันเพื่อเสริมศักยภาพนักเรียนผ่าน Statorials. รู้เพิ่มเติม