วิธีการใช้ทฤษฎีบทของ chebyshev ใน excel

ทฤษฎีบทของเชบีเชฟ ระบุว่าสำหรับจำนวน k ใดๆ ที่มากกว่า 1 ค่าข้อมูลอย่างน้อย 1 – 1/k ² ในการแจกแจงที่ได้รับการฝึกจะอยู่ภายในค่าเบี่ยงเบนมาตรฐาน k จากค่าเฉลี่ย

เช่น สำหรับการแจกแจงรูปทรงใดๆ อย่างน้อย 1 – 1/3 ² = 88.89% ของค่าในการแจกแจงจะอยู่ภายใน 3 ส่วนเบี่ยงเบนมาตรฐานของค่าเฉลี่ย

บทช่วยสอนนี้สาธิตตัวอย่างการประยุกต์ใช้ทฤษฎีบทของ Chebyshev ใน Excel

ตัวอย่างที่ 1: ใช้ทฤษฎีบทของ Chebyshev เพื่อกำหนดว่าเปอร์เซ็นต์ของค่าจะอยู่ระหว่าง 30 ถึง 70 สำหรับชุดข้อมูลที่มีค่าเฉลี่ย 50 และค่าเบี่ยงเบนมาตรฐาน 10

ขั้นแรก ให้กำหนดค่าของ k เราสามารถทำได้โดยระบุค่าเบี่ยงเบนมาตรฐานระหว่าง 30 ถึง 70 จากค่าเฉลี่ย:

(30 – ค่าเฉลี่ย) / ส่วนเบี่ยงเบนมาตรฐาน = (30 – 50) / 10 = -20 / 10 = -2

(70 – ค่าเฉลี่ย) / ส่วนเบี่ยงเบนมาตรฐาน = (70 – 50) / 10 = 20 / 10 = 2

ค่า 30 และ 70 คือค่าเบี่ยงเบนมาตรฐาน 2 ค่าที่ต่ำกว่าและสูงกว่าค่าเฉลี่ยตามลำดับ ดังนั้น k = 2 .

จากนั้นเราสามารถใช้สูตรต่อไปนี้ใน Excel เพื่อค้นหาเปอร์เซ็นต์ขั้นต่ำของค่าที่อยู่ภายใน 2 ส่วนเบี่ยงเบนมาตรฐานของค่าเฉลี่ยสำหรับชุดข้อมูลนี้:

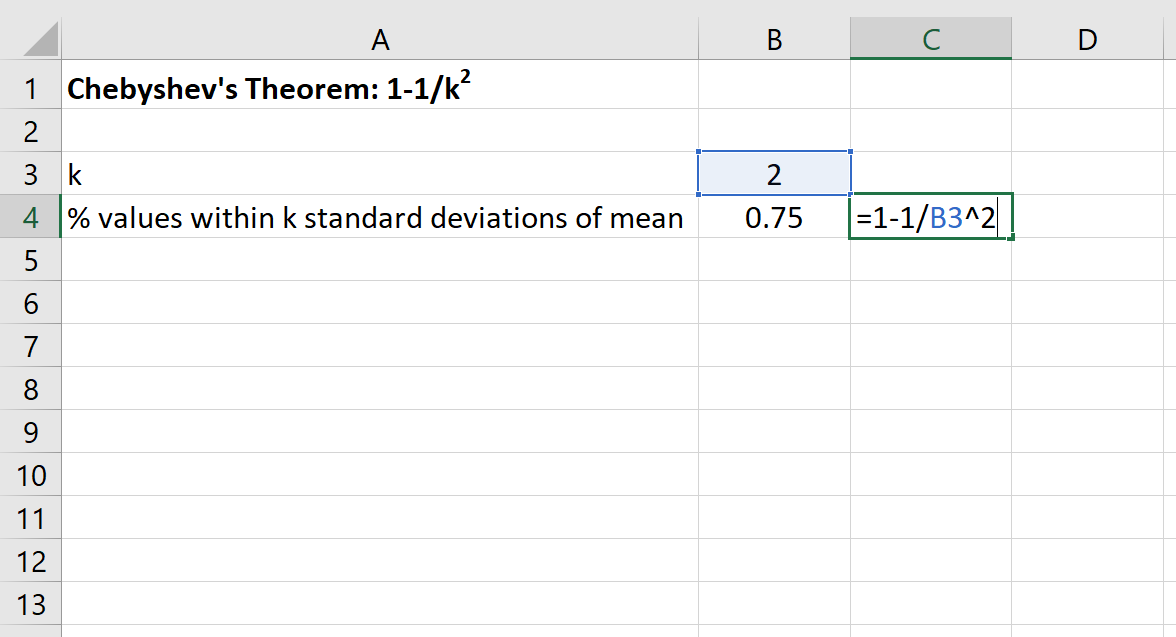
เปอร์เซ็นต์ของค่าระหว่าง 30 ถึง 70 สำหรับชุดข้อมูลนี้จะมี อย่างน้อย 75%

ตัวอย่างที่ 2: ใช้ทฤษฎีบทของ Chebyshev เพื่อกำหนดว่าเปอร์เซ็นต์ของค่าจะอยู่ระหว่าง 20 ถึง 50 สำหรับชุดข้อมูลที่มีค่าเฉลี่ย 35 และค่าเบี่ยงเบนมาตรฐาน 5

ขั้นแรก ให้กำหนดค่าของ k เราสามารถทำได้โดยกำหนดว่าค่าเบี่ยงเบนมาตรฐานอยู่ระหว่าง 20 ถึง 50 จากค่าเฉลี่ย:

(20 – ค่าเฉลี่ย) / ส่วนเบี่ยงเบนมาตรฐาน = (20 – 35) / 5 = -15 / 5 = -3

(50 – ค่าเฉลี่ย) / ส่วนเบี่ยงเบนมาตรฐาน = (50 – 35) / 5 = 15 / 5 = 3

ค่า 20 และ 50 คือค่าเบี่ยงเบนมาตรฐาน 3 ค่าที่ต่ำกว่าและสูงกว่าค่าเฉลี่ยตามลำดับ ดังนั้น k = 3 .

จากนั้นเราสามารถใช้สูตรต่อไปนี้ใน Excel เพื่อค้นหาเปอร์เซ็นต์ขั้นต่ำของค่าที่อยู่ภายใน 3 ส่วนเบี่ยงเบนมาตรฐานของค่าเฉลี่ยสำหรับชุดข้อมูลนี้:

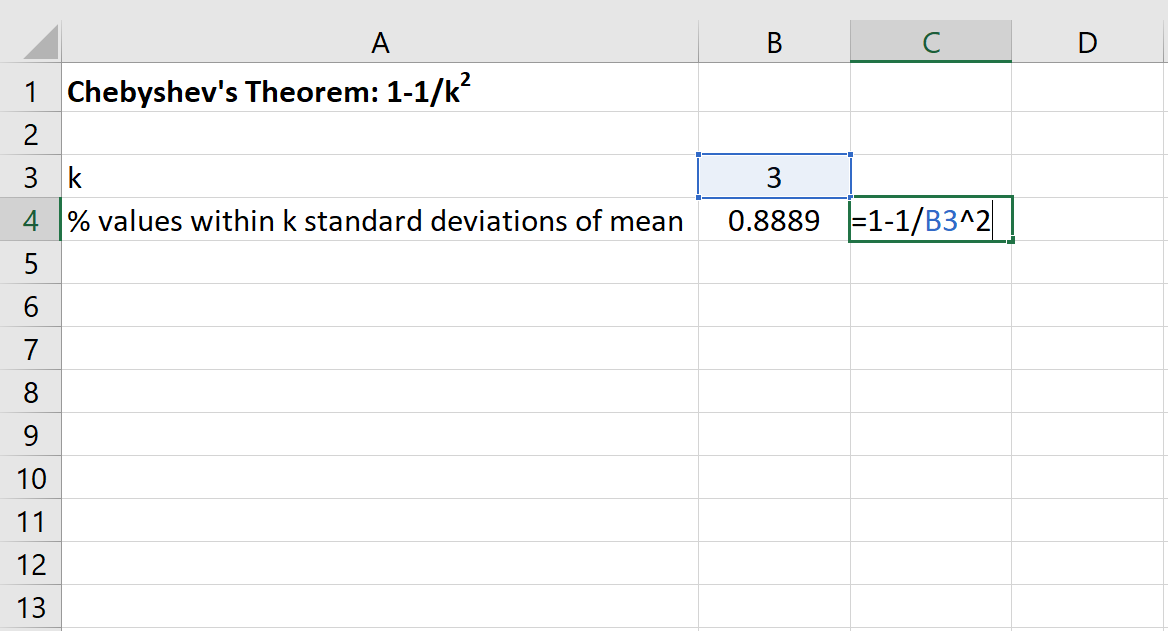
เปอร์เซ็นต์ของค่าระหว่าง 20 ถึง 50 สำหรับชุดข้อมูลนี้จะมี อย่างน้อย 88.89%

ตัวอย่างที่ 3: ใช้ทฤษฎีบทของ Chebyshev เพื่อกำหนดว่าเปอร์เซ็นต์ของค่าจะอยู่ระหว่าง 80 ถึง 120 สำหรับชุดข้อมูลที่มีค่าเฉลี่ย 100 และค่าเบี่ยงเบนมาตรฐานคือ 5

ขั้นแรก ให้กำหนดค่าของ k เราสามารถทำได้โดยระบุค่าเบี่ยงเบนมาตรฐานระหว่าง 80 ถึง 120 จากค่าเฉลี่ย:

(80 – ค่าเฉลี่ย) / ส่วนเบี่ยงเบนมาตรฐาน = (80 – 100) / 5 = -20 / 5 = -4

(120 – ค่าเฉลี่ย) / ส่วนเบี่ยงเบนมาตรฐาน = (120 – 100) / 5 = 20 / 5 = 4

ค่า 80 และ 120 มีค่าเบี่ยงเบนมาตรฐาน 4 ค่าต่ำกว่าและสูงกว่าค่าเฉลี่ยตามลำดับ ดังนั้น k = 4 .

จากนั้นเราสามารถใช้สูตรต่อไปนี้ใน Excel เพื่อค้นหาเปอร์เซ็นต์ขั้นต่ำของค่าที่อยู่ภายใน 4 ส่วนเบี่ยงเบนมาตรฐานของค่าเฉลี่ยสำหรับชุดข้อมูลนี้:

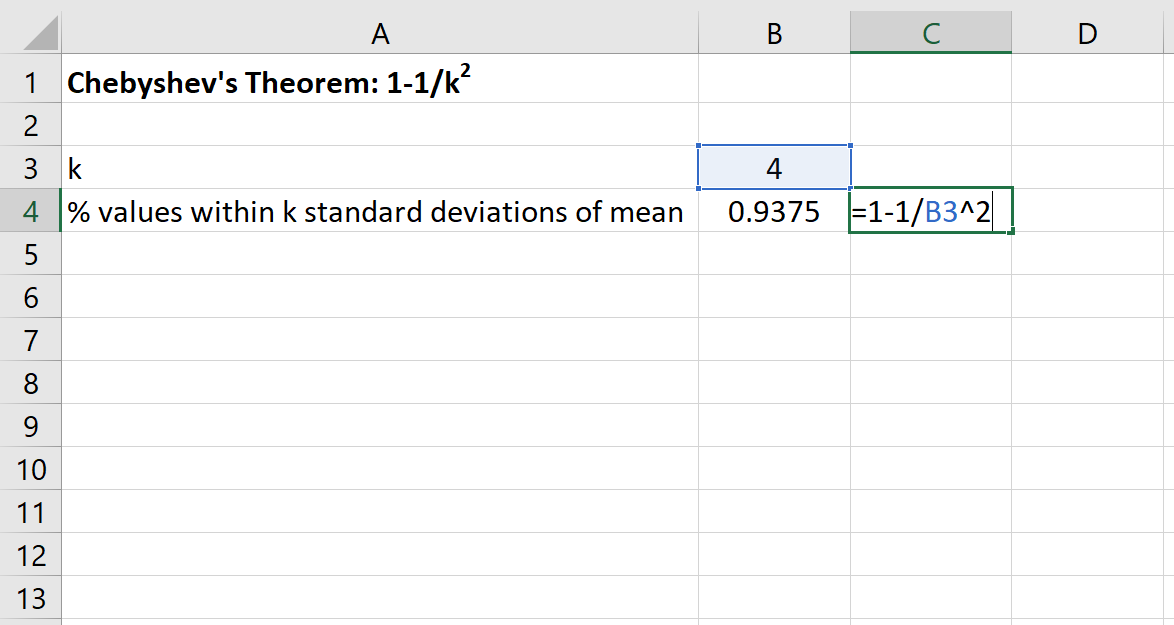
เปอร์เซ็นต์ของค่าระหว่าง 80 ถึง 120 สำหรับชุดข้อมูลนี้จะมี อย่างน้อย 93.75%