วิธีการใช้ทฤษฎีบทขีด จำกัด กลางใน r (พร้อมตัวอย่าง)

ทฤษฎีบทขีดจำกัดกลาง ระบุว่า การกระจายตัว ตัวอย่างของค่าเฉลี่ยตัวอย่างจะอยู่ที่ประมาณปกติ หากขนาดตัวอย่างมีขนาดใหญ่เพียงพอ แม้ว่าการกระจายตัวของประชากรจะไม่ปกติก็ตาม

ทฤษฎีบทขีดจำกัดกลางยังระบุด้วยว่าการกระจายตัวอย่างจะมีคุณสมบัติดังต่อไปนี้:

1. ค่าเฉลี่ยของการกระจายตัวอย่างจะเท่ากับค่าเฉลี่ยของการกระจายตัวของประชากร:

x = ไมโคร

2. ค่าเบี่ยงเบนมาตรฐานของการกระจายตัวอย่างจะเท่ากับค่าเบี่ยงเบนมาตรฐานของการกระจายตัวของประชากรหารด้วยขนาดตัวอย่าง:

s = σ /n

ตัวอย่างต่อไปนี้แสดงวิธีการใช้ทฤษฎีบทขีดจำกัดกลางใน R

ตัวอย่าง: การประยุกต์ใช้ทฤษฎีบทขีดจำกัดกลางใน R

สมมติว่าความกว้างของกระดองเต่ามี การกระจายสม่ำเสมอ โดยมีความกว้างขั้นต่ำ 2 นิ้ว และความกว้างสูงสุด 6 นิ้ว

นั่นคือถ้าเราเลือกเต่าโดยการสุ่มและวัดความกว้างของกระดอง มันก็มีแนวโน้มที่จะมี ความกว้าง ระหว่าง 2 ถึง 6 นิ้วด้วย.

รหัสต่อไปนี้แสดงวิธีสร้างชุดข้อมูลใน R ที่มีการวัดความกว้างกระดองของเต่า 1,000 ตัว โดยกระจายเท่าๆ กันระหว่าง 2 ถึง 6 นิ้ว:

 #make this example reproducible
set. seeds (0)

#create random variable with sample size of 1000 that is uniformly distributed
data <- runif(n=1000, min=2, max=6)

#create histogram to visualize distribution of turtle shell widths
hist(data, col=' steelblue ', main=' Histogram of Turtle Shell Widths ')

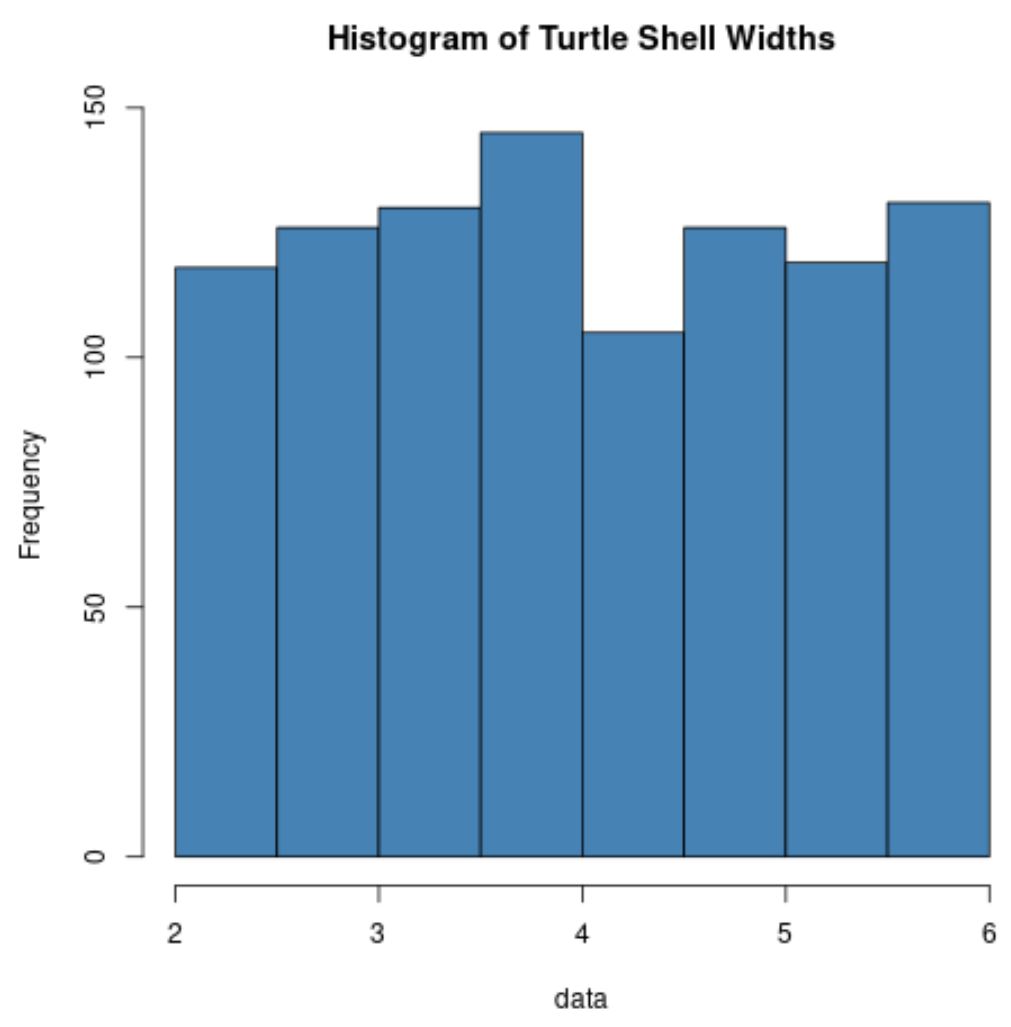
โปรดทราบว่าการกระจายความกว้างของกระดองเต่าโดยปกติจะไม่กระจายเลย

ทีนี้ ลองจินตนาการว่าเราสุ่มตัวอย่างเต่า 5 ตัวจากประชากรกลุ่มนี้ และวัดค่าเฉลี่ยตัวอย่างซ้ำแล้วซ้ำอีก

รหัสต่อไปนี้แสดงวิธีดำเนินการกระบวนการนี้ใน R และสร้างฮิสโตแกรมเพื่อแสดงภาพการกระจายตัวของค่าเฉลี่ยตัวอย่าง:

 #create empty vector to hold sample means
sample5 <- c()

#take 1,000 random samples of size n=5
n = 1000
for (i in 1:n){
sample5[i] = mean(sample(data, 5, replace= TRUE ))
}

#calculate mean and standard deviation of sample means
mean(sample5)

[1] 4.008103

sd(sample5)

[1] 0.5171083 

#create histogram to visualize sampling distribution of sample means
hist(sample5, col = ' steelblue ', xlab=' Turtle Shell Width ', main=' Sample size = 5 ') 

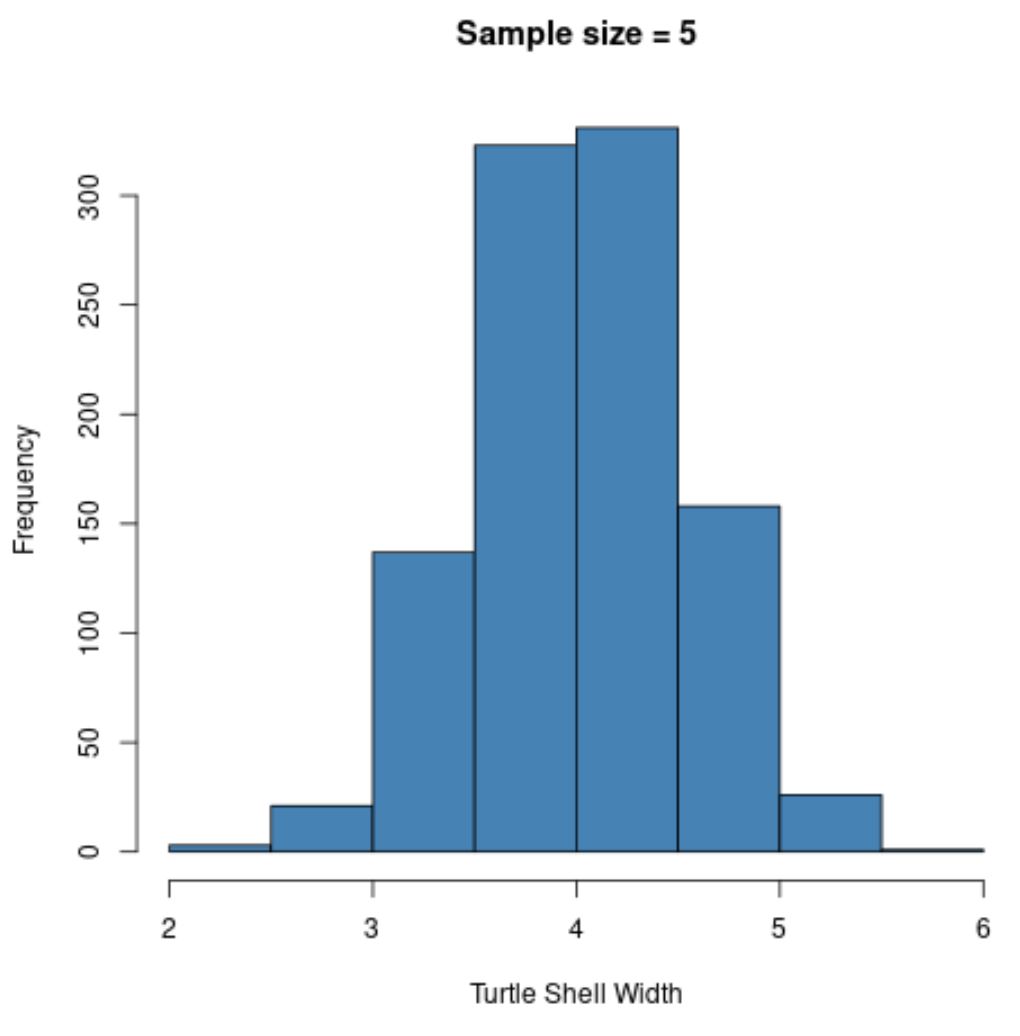
โปรดทราบว่าการกระจายตัวตัวอย่างของวิธีการตัวอย่างปรากฏว่ามีการกระจายตามปกติ แม้ว่าการกระจายตัวอย่างที่ได้มาจะไม่ได้กระจายตามปกติก็ตาม

นอกจากนี้ ให้สังเกตค่าเฉลี่ยตัวอย่างและค่าเบี่ยงเบนมาตรฐานตัวอย่างสำหรับการแจกแจงตัวอย่างนี้ด้วย:

• x̄ : 4.008
• ส : 0.517

ตอนนี้ สมมติว่าเราเพิ่มขนาดตัวอย่างที่เราใช้จาก n=5 เป็น n=30 และสร้างฮิสโตแกรมของค่าเฉลี่ยตัวอย่างขึ้นมาใหม่:

 #create empty vector to hold sample means
sample30 <- c()

#take 1,000 random samples of size n=30
n = 1000
for (i in 1:n){
sample30[i] = mean(sample(data, 30, replace= TRUE ))
}

#calculate mean and standard deviation of sample means
mean(sample30)

[1] 4.000472

sd(sample30)

[1] 0.2003791

#create histogram to visualize sampling distribution of sample means
hist(sample30, col = ' steelblue ', xlab=' Turtle Shell Width ', main=' Sample size = 30 ') 

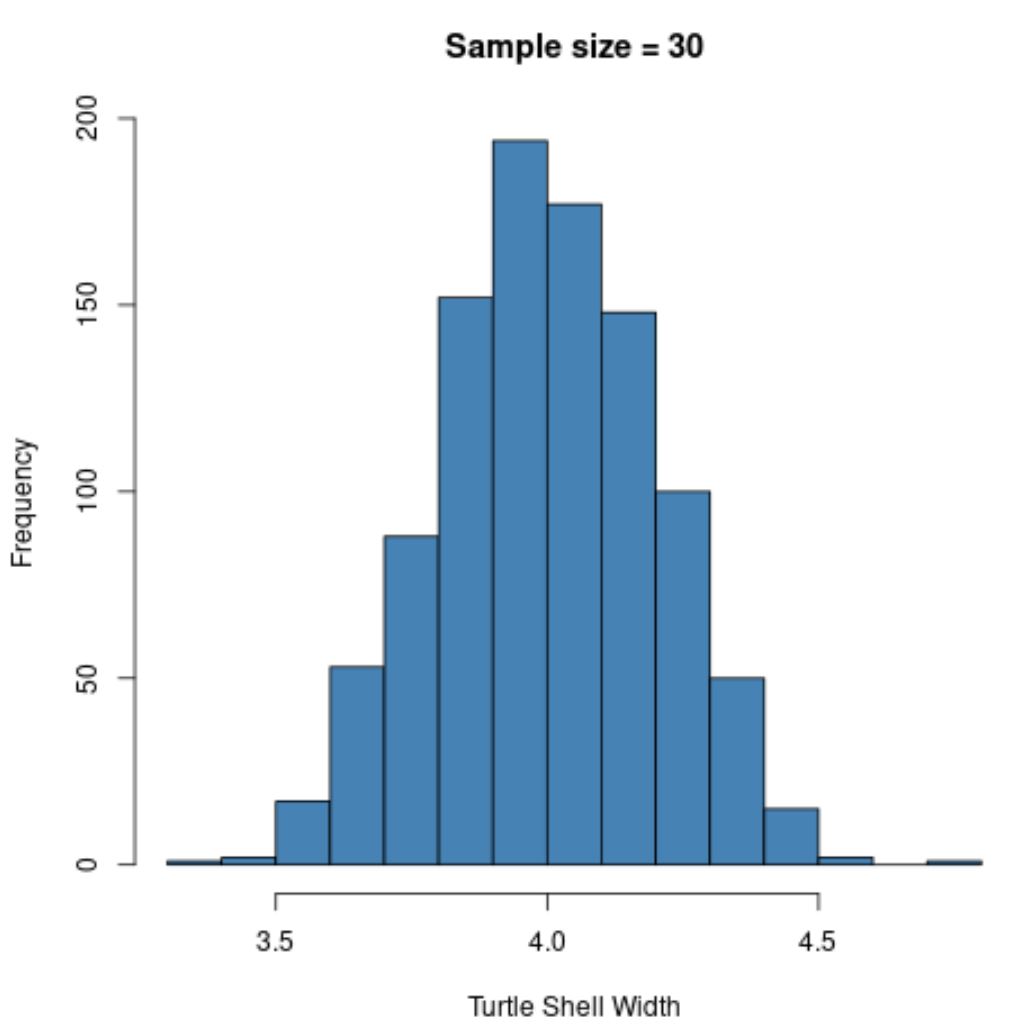
การกระจายตัวอย่างจะ มีการกระจายตามปกติ อีกครั้ง แต่ค่าเบี่ยงเบนมาตรฐานของกลุ่มตัวอย่างยังน้อยกว่า:

• วิ : 0.200

เนื่องจากเราใช้ขนาดตัวอย่างที่ใหญ่กว่า (n=30) เมื่อเทียบกับตัวอย่างก่อนหน้า (n=5) ดังนั้นค่าเบี่ยงเบนมาตรฐานของค่าเฉลี่ยตัวอย่างจึงน้อยกว่าด้วยซ้ำ

หากเรายังคงใช้ตัวอย่างที่ใหญ่ขึ้นเรื่อยๆ เราจะพบว่าค่าเบี่ยงเบนมาตรฐานของกลุ่มตัวอย่างนั้นเล็กลงเรื่อยๆ

นี่แสดงให้เห็นถึงทฤษฎีบทขีดจำกัดกลางในทางปฏิบัติ

แหล่งข้อมูลเพิ่มเติม

แหล่งข้อมูลต่อไปนี้ให้ข้อมูลเพิ่มเติมเกี่ยวกับทฤษฎีบทขีดจำกัดกลาง:

ความรู้เบื้องต้นเกี่ยวกับทฤษฎีบทขีดจำกัดศูนย์กลาง
เครื่องคำนวณทฤษฎีบทขีดจำกัดกลาง
5 ตัวอย่างการใช้ทฤษฎีบทขีดจำกัดกลางในชีวิตจริง