ทฤษฎีบทขีดจำกัดกลาง

โดย ดร.เบนจามิน แอนเดอร์สัน สิงหาคม 1, 2023 ความน่าจะเป็น 0 ความคิดเห็น

บทความนี้จะอธิบายว่าทฤษฎีบทขีดจำกัดกลาง (CLT) คืออะไร และใช้เพื่ออะไรในสถิติ นอกจากนี้คุณยังจะพบว่าสูตรของทฤษฎีบทขีด จำกัด จุดศูนย์กลางคืออะไรและตัวอย่างการประยุกต์ใช้ได้รับการแก้ไขทีละขั้นตอน

ทฤษฎีบทขีด จำกัด จุดศูนย์กลางคืออะไร?

ในสถิติ ทฤษฎีบทขีดจำกัดกลาง หรือที่เรียกว่า ทฤษฎีบทขีดจำกัดกลาง ระบุว่า การกระจายตัวของค่าเฉลี่ยตัวอย่าง เข้าใกล้การแจกแจงแบบปกติเมื่อขนาดตัวอย่างเพิ่มขึ้น โดยไม่คำนึงถึง การกระจายตัวของความน่าจะเป็น ของประชากร

นั่นคือ ทฤษฎีบทขีดจำกัดศูนย์กลางบอกว่าถ้าเราหาตัวอย่างจำนวนมากเพียงพอ ค่าเฉลี่ยของกลุ่มตัวอย่างเหล่านั้นก็สามารถประมาณได้ด้วยการแจกแจงแบบปกติ

นอกจากนี้ ทฤษฎีบทขีดจำกัดกลางระบุว่าค่าเฉลี่ยตัวอย่างจะเข้าใกล้ค่าเฉลี่ยประชากรเมื่อขนาดตัวอย่างเพิ่มขึ้น ซึ่งช่วยให้เราสามารถประมาณค่าพารามิเตอร์ของประชากรทางสถิติได้ ด้านล่างเราจะดูวิธีการทำสิ่งนี้

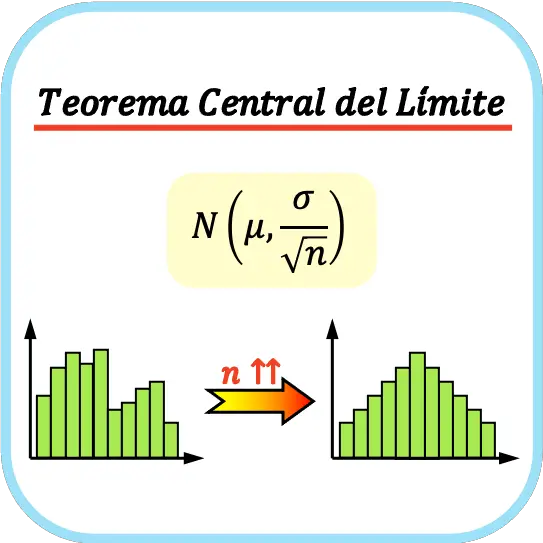
โดยทั่วไป ถือว่าการใช้ทฤษฎีบทขีดจำกัดกลาง ขนาดของกลุ่มตัวอย่างจะต้องมีการสังเกตอย่างน้อย 30 ครั้ง แม้ว่าจะขึ้นอยู่กับลักษณะของตัวแปรที่ศึกษาก็ตาม

ทฤษฎีบทขีดจำกัดศูนย์กลางมีการนำไปใช้ได้หลายอย่าง เนื่องจากการแจกแจงแบบปกติทำให้สามารถคำนวณทางสถิติเชิงอนุมานได้ เช่น การทดสอบสมมติฐานหรือช่วงความเชื่อมั่น ตัวอย่างเช่น ในด้านการเงิน ทฤษฎีบทขีดจำกัดกลางใช้เพื่อวิเคราะห์ผลตอบแทนและความเสี่ยงของการลงทุน

➤ ดู: การแจกแจงแบบปกติคืออะไร?

ตัวอย่างทฤษฎีบทขีดจำกัดจุดศูนย์กลาง

เมื่อเราได้เห็นคำจำกัดความของทฤษฎีบทขีดจำกัดจุดศูนย์กลางแล้ว เรามาดูตัวอย่างเพื่อทำความเข้าใจความหมายของทฤษฎีบทนี้กัน

ตัวอย่างของทฤษฎีบทขีดจำกัดจุดศูนย์กลางคือการทอยลูกเต๋า ลูกกลิ้งแม่พิมพ์มี การกระจายสม่ำเสมอสม่ำเสมอ เนื่องจากผลลัพธ์ทั้งหมดมีความเหมาะสม แต่การกระจายตัวของผลรวมของผลลัพธ์หลายรายการเข้าใกล้การแจกแจงแบบปกติ

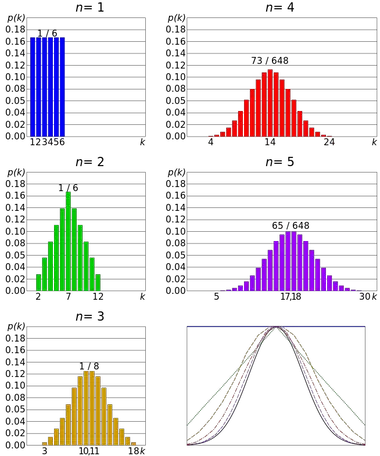
ดังนั้น ยิ่งมีการโยนมากเท่าใด รูปร่างของการแจกแจงของค่าเฉลี่ยก็จะมีแนวโน้มคล้ายกับกราฟของการแจกแจงแบบปกติมากขึ้นเท่านั้น

สูตรทฤษฎีบทขีดจำกัดกลาง

ทฤษฎีบทขีดจำกัดกลางระบุว่าหากประชากรมีค่าเฉลี่ย μ และค่าเบี่ยงเบนมาตรฐาน σ และเราหาตัวอย่างจำนวนมากเพียงพอ (n≥30) ชุดของค่าเฉลี่ยตัวอย่างสามารถประมาณได้กับการแจกแจงแบบปกติด้วยค่าเฉลี่ย μ และค่าเบี่ยงเบนมาตรฐาน σ /√น.

$\displaystyle N\left(\mu,\frac{\sigma}{\sqrt{n}}\right)$

นอกจากนี้ ถ้า X ₁ _{เป็นการ} แจกแจงแบบปกติที่กำหนดโดยสูตรต่อไปนี้ _:

$\displaystyle Y=\sum_{i=1}^n X_i \sim N\left(n\cdot \mu,\sigma \cdot \sqrt{n}\right)$

แก้แบบฝึกหัดของทฤษฎีบทขีดจำกัดกลาง

เพื่อให้คุณสามารถซึมซับแนวคิดนี้ได้อย่างเต็มที่ ต่อไปนี้คือแบบฝึกหัดแก้ไขของทฤษฎีบทขีดจำกัดจุดศูนย์กลาง

บริษัทแห่งหนึ่งจำหน่ายชิ้นส่วนที่ใช้ทดแทนส่วนประกอบของเล่นบางอย่าง เหรียญมีน้ำหนักเฉลี่ย 300 กรัม และส่วนเบี่ยงเบนมาตรฐาน 50 กรัม หากลูกค้าสั่งชุดละ 100 ชิ้น ความน่าจะเป็นที่น้ำหนักเฉลี่ยของชิ้นในชุดจะมากกว่า 305 กรัม เป็นเท่าใด และความน่าจะเป็นที่ชุด 100 ชิ้นจะมีน้ำหนักมากกว่า 31 กิโลกรัมเป็นเท่าใด

เนื่องจากขนาดแบทช์มีขนาดใหญ่ (n=100) เราจึงสามารถใช้ทฤษฎีบทขีดจำกัดกลางเพื่อแก้ปัญหาได้

ดังนั้น เมื่อใช้สูตรทฤษฎีบทขีดจำกัดกลาง การกระจายตัวของค่าเฉลี่ยตัวอย่างสามารถประมาณได้กับการแจกแจงแบบปกติด้วยพารามิเตอร์ต่อไปนี้

$\displaystyle N\left(\mu,\frac{\sigma}{\sqrt{n}}\right)$

$\mu_{\overline{X}}=\mu=300$

$\sigma_{\overline{X}}=\cfrac{\sigma}{\sqrt{n}}=\cfrac{50}{\sqrt{100}}=5$

$\displaystyle N\left(300,5\right)$

ตอนนี้เราดำเนินการขั้นตอนการพิมพ์เพื่อที่เราจะสามารถค้นหาความน่าจะเป็นที่แบบฝึกหัดขอให้เราทำได้ ในการทำเช่นนี้ เราต้องลบค่าเฉลี่ยจากการแจกแจงแล้วหารด้วยค่าเบี่ยงเบนมาตรฐาน:

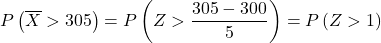$\displaystyle P\left(\overline{X}>305\right)=P\left(Z>\frac{305-300}{5}\right)=P\left(Z>1\right)” title=”Rendered by QuickLaTeX.com” height=”43″ width=”381″ style=”vertical-align: -17px;”> ดังนั้น เพื่อหาความน่าจะเป็นที่น้ำหนักเฉลี่ยของชิ้นส่วนในล็อตมากกว่า 305 กรัม เราต้องดูว่าค่า Z>1 สอดคล้องกับค่าใดใน <a href=$ ตารางการแจกแจงปกติ :

$\displaystyle P\left(\overline{X}>305\right)=P\left(Z>1\right)=0,1587″ title=”Rendered by QuickLaTeX.com” height=”22″ width=”276″ style=”vertical-align: -7px;”> ในทางกลับกัน ต้องขอบคุณทฤษฎีบทขีดจำกัดศูนย์กลางที่ทำให้เราสามารถรู้ได้ว่าเหรียญ 100 ชุดสามารถเข้าใกล้การแจกแจงแบบปกติได้ เนื่องจากเหรียญทั้งหมดมีการกระจายตัวแบบเดียวกัน ดังนั้น เพื่อพิจารณาความน่าจะเป็นที่เหรียญ 100 ชุดจะมีน้ำหนักมากกว่า 31 กิโลกรัม เราจึงต้องใช้สูตรอื่นของทฤษฎีบทขีดจำกัดศูนย์กลาง: <p class=$ $\displaystyle Y=\sum_{i=1}^n X_i \sim N\left(n\cdot \mu,\sigma \cdot \sqrt{n}\right)$

$\displaystyle Y\sim N\left(100\cdot 300,50\cdot \sqrt{100}\right)$

$\displaystyle Y\sim N\left(30000,500\right)$

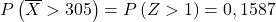
ดังนั้นเราจึงทำซ้ำขั้นตอนการพิมพ์ จากนั้นค้นหาความน่าจะเป็นที่สองที่ปัญหาถามเรา:

$\displaystyle P\left(Y>31000\right)=P\left(Z>\frac{31000-30000}{500}\right)=P\left(Z>2\right)” title=”Rendered by QuickLaTeX.com” height=”43″ width=”430″ style=”vertical-align: -17px;”> สุดท้ายนี้ เราสามารถระบุความน่าจะเป็นที่ชุดสินค้า 100 ชิ้นจะมีน้ำหนักมากกว่า 31 กก. 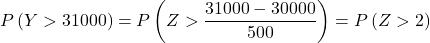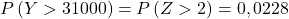โดยใช้ตารางการกระจายแบบปกติ: 31000\right)=P\left(Z>2\right)=0,0228″ title=”Rendered by QuickLaTeX.com” height=”19″ width=”289″ style=”vertical-align: -5px;”> <div style=$ ➤ ดู: กฎของจำนวนมาก

เกี่ยวกับผู้แต่ง

ดร.เบนจามิน แอนเดอร์สัน

สวัสดี ฉันชื่อเบนจามิน ศาสตราจารย์สถิติเกษียณอายุแล้ว และผันตัวมาเป็นครูสอนสถิติโดยเฉพาะ ด้วยประสบการณ์และความเชี่ยวชาญที่กว้างขวางในสาขาสถิติ ฉันกระตือรือร้นที่จะแบ่งปันความรู้ของฉันเพื่อเสริมศักยภาพนักเรียนผ่าน Statorials. รู้เพิ่มเติม