ฟังก์ชันความน่าจะเป็น

โดย ดร.เบนจามิน แอนเดอร์สัน สิงหาคม 5, 2023 ความน่าจะเป็น 0 ความคิดเห็น

บทความนี้จะอธิบายว่าฟังก์ชันความน่าจะเป็นคืออะไร ดังนั้น คุณจะพบความหมายของฟังก์ชันความน่าจะเป็น คุณสมบัติของฟังก์ชัน และตัวอย่างที่ชัดเจนในการคำนวณฟังก์ชันความน่าจะเป็น นอกจากนี้ ยังมีการนำเสนอความแตกต่างระหว่างฟังก์ชันความน่าจะเป็นและฟังก์ชันความน่าจะเป็นประเภทอื่นๆ อีกด้วย

ฟังก์ชันความน่าจะเป็นคืออะไร?

ฟังก์ชันความน่าจะ เป็น หรือที่เรียกว่า ฟังก์ชันมวลความน่า จะเป็น เป็นฟังก์ชันทางคณิตศาสตร์ที่อธิบายความน่าจะเป็นที่ตัวแปรสุ่มแบบไม่ต่อเนื่องรับค่าที่กำหนด

นั่นคือ ฟังก์ชันความน่าจะเป็นจะส่งกลับค่าความน่าจะเป็นที่เกี่ยวข้องกับตัวแปรที่ไม่ต่อเนื่องซึ่งมีค่าเท่ากับค่าหนึ่งทุกประการ

$f(x)=P[X=x]$

ตัวอย่างเช่น ความน่าจะเป็นที่จะทอยตัวเลขใดๆ เมื่อทอยลูกเต๋าคือ 1/6 (ลูกเต๋ามีหกด้าน) ดังนั้น ฟังก์ชันความน่าจะเป็นที่เกี่ยวข้องกับพื้นที่ตัวอย่างนี้จะเท่ากับ 1/6 สำหรับ n ไม่ว่าค่าใดก็ตาม

คุณสมบัติของฟังก์ชันความน่าจะเป็น

ฟังก์ชันความน่าจะเป็นมีคุณสมบัติดังต่อไปนี้:

ความน่าจะเป็นต้องไม่เป็นลบ ดังนั้นฟังก์ชันความน่าจะเป็นจึงเป็นศูนย์หรือบวกสำหรับค่า x ใดๆ

$f(x)\geq 0$

ในทำนองเดียวกัน ความน่าจะเป็นสูงสุดคือความสามัคคี ซึ่งหมายความว่าเหตุการณ์จะเกิดขึ้นเสมอ ดังนั้นค่าสูงสุดของฟังก์ชันความน่าจะเป็นจึงเท่ากับ 1

$f(x)\leq 1$

ในที่สุด ผลรวมของค่าทั้งหมดของฟังก์ชันความน่าจะเป็นให้ 1 เนื่องจากมันคือผลรวมของความน่าจะเป็นทั้งหมดในพื้นที่ตัวอย่าง

$\displaystyle \sum_{i=1}^{+\infty}f(x_i)=\sum_{i=1}^{+\infty}p_i=1$

ตัวอย่างฟังก์ชันความน่าจะเป็น

ตอนนี้เรารู้คำจำกัดความและคุณลักษณะของฟังก์ชันความน่าจะเป็นแล้ว เรามาดูตัวอย่างฟังก์ชันความน่าจะเป็นประเภทนี้กัน

คำนวณความน่าจะเป็นที่จะได้หัว 0, 1, 2, 3 และ 4 ครั้งโดยการพลิกเหรียญอิสระสี่ครั้ง ต่อไป ให้สร้างกราฟฟังก์ชันความน่าจะเป็นที่พบ

ก่อนอื่น เราต้องคำนวณความน่าจะเป็นที่จะได้หัว เมื่อต้องการทำเช่นนี้ เราต้องหารกรณีที่เป็นไปได้ด้วยจำนวนกรณีทั้งหมด คุณสามารถดูการคำนวณความน่าจะเป็นทั้งหมดได้ในตารางต่อไปนี้:

และเมื่อเราคำนวณความน่าจะเป็นทั้งหมดแล้ว เราก็สามารถแสดงค่าของฟังก์ชันความน่าจะเป็นบนกราฟได้:

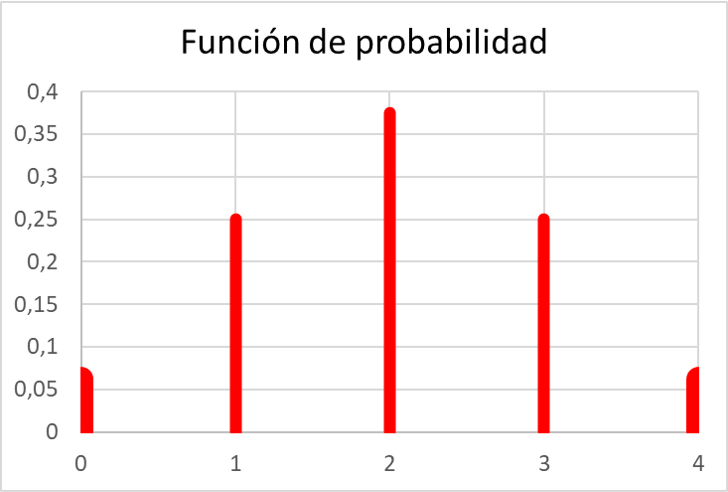
อย่างที่คุณเห็น ฟังก์ชันความน่าจะเป็นในแบบฝึกหัดมีคุณสมบัติตรงตามคุณสมบัติทั้งหมดของฟังก์ชันความน่าจะเป็น เนื่องจากค่าทั้งหมดอยู่ระหว่าง 0 ถึง 1 และยิ่งไปกว่านั้น ผลรวมของค่าทั้งหมดจะเท่ากับ 1

ฟังก์ชันความน่าจะเป็นและฟังก์ชันความหนาแน่น

ในส่วนนี้ เราจะเห็นความแตกต่างระหว่างฟังก์ชันความน่าจะเป็นและฟังก์ชันความหนาแน่น เนื่องจากเป็นฟังก์ชันความน่าจะเป็นสองประเภทที่มีจุดประสงค์เดียวกันแต่ใช้ในกรณีต่างกัน

ความแตกต่างระหว่างฟังก์ชันความน่าจะเป็นและฟังก์ชันความหนาแน่น คือประเภทของตัวแปรที่อธิบายความน่าจะเป็น ฟังก์ชันความน่าจะเป็นใช้เพื่อกำหนดความน่าจะเป็นของตัวแปรที่ไม่ต่อเนื่อง ในขณะที่ฟังก์ชันความหนาแน่นใช้เพื่อกำหนดความน่าจะเป็นของตัวแปรต่อเนื่อง

ดังนั้น จะใช้ฟังก์ชันความน่าจะเป็นหรือฟังก์ชันความหนาแน่น ขึ้นอยู่กับตัวแปร

หากต้องการเรียนรู้เพิ่มเติมเกี่ยวกับฟังก์ชันความหนาแน่น ให้คลิกลิงก์ต่อไปนี้:

➤ ดูที่: ฟังก์ชันความหนาแน่นของความน่าจะเป็น

ฟังก์ชันความน่าจะเป็นและฟังก์ชันการแจกแจง

ความแตกต่างระหว่างฟังก์ชันความน่าจะเป็นและฟังก์ชันการแจกแจง คือประเภทของความน่าจะเป็นที่ฟังก์ชันดังกล่าวกำหนด ฟังก์ชันความน่าจะเป็นจะระบุถึงความน่าจะเป็นที่ตัวแปรจะใช้กับค่าที่กำหนด ในขณะที่ฟังก์ชันการแจกแจงจะอธิบายความน่าจะเป็นสะสมของตัวแปร

ดังนั้นฟังก์ชันการแจกแจงจึงคำนวณจากฟังก์ชันความน่าจะเป็น

ตามตัวอย่าง ในลิงก์ต่อไปนี้ คุณสามารถดูการคำนวณฟังก์ชันการแจกแจงเพื่อให้ได้หัวจากการโยนเหรียญสี่ครั้ง โดยอิงตามฟังก์ชันความน่าจะเป็นที่พบในแบบฝึกหัดด้านบน

➤ ดู: ตัวอย่างฟังก์ชันการกระจาย

เกี่ยวกับผู้แต่ง

ดร.เบนจามิน แอนเดอร์สัน

สวัสดี ฉันชื่อเบนจามิน ศาสตราจารย์สถิติเกษียณอายุแล้ว และผันตัวมาเป็นครูสอนสถิติโดยเฉพาะ ด้วยประสบการณ์และความเชี่ยวชาญที่กว้างขวางในสาขาสถิติ ฉันกระตือรือร้นที่จะแบ่งปันความรู้ของฉันเพื่อเสริมศักยภาพนักเรียนผ่าน Statorials. รู้เพิ่มเติม