ฟังก์ชันความหนาแน่น

โดย ดร.เบนจามิน แอนเดอร์สัน สิงหาคม 5, 2023 ความน่าจะเป็น 0 ความคิดเห็น

ในบทความนี้ คุณจะค้นพบว่าฟังก์ชันความหนาแน่นคืออะไร ความน่าจะเป็นคำนวณจากฟังก์ชันความหนาแน่นได้อย่างไร และคุณลักษณะของฟังก์ชันความน่าจะเป็นนี้ นอกจากนี้ คุณยังจะได้เห็นความแตกต่างระหว่างฟังก์ชันความหนาแน่นและฟังก์ชันการกระจายอีกด้วย

ฟังก์ชันความหนาแน่นคืออะไร?

ฟังก์ชันความหนาแน่น หรือที่เรียกว่า ฟังก์ชันความหนาแน่นของความน่าจะ เป็น เป็นฟังก์ชันทางคณิตศาสตร์ที่อธิบายความน่าจะเป็นที่ตัวแปรสุ่มแบบต่อเนื่องจะใช้กับค่าที่กำหนด

กล่าวอีกนัยหนึ่ง ฟังก์ชันความหนาแน่นที่เกี่ยวข้องกับตัวแปรจะกำหนดความน่าจะเป็นที่ตัวแปรรับค่าทางคณิตศาสตร์

ตัวอย่างเช่น สมมติว่าความน่าจะเป็นที่ผู้ใหญ่จะสูงกว่า 1.80 เมตรในประชากรคือ 35% จากนั้นฟังก์ชันความหนาแน่นจะระบุความน่าจะเป็น 35% เมื่อคำนวณความน่าจะเป็นดังกล่าว

บางครั้งฟังก์ชันความหนาแน่นของความน่าจะเป็นจะใช้ตัวย่อเป็น PDF

คำนวณความน่าจะเป็นด้วยฟังก์ชันความหนาแน่น

ในการค้นหาความน่าจะเป็นที่ตัวแปรต่อเนื่องรับค่าในช่วงเวลาหนึ่ง จำเป็นต้องคำนวณอินทิกรัลของฟังก์ชันความหนาแน่นที่เกี่ยวข้องกับตัวแปรดังกล่าวระหว่างขีดจำกัดของช่วงเวลา

$\displaystyle P[a\leq X\leq b]=\int_a^b f(x)dx$

ทอง

$f(x)$

คือฟังก์ชันความหนาแน่นของตัวแปรสุ่มต่อเนื่อง

หรืออีกนัยหนึ่ง ความน่าจะเป็นที่ตัวแปรรับค่าในช่วงเวลาหนึ่งจะเท่ากับพื้นที่ใต้ฟังก์ชันความหนาแน่นในช่วงเวลานั้น

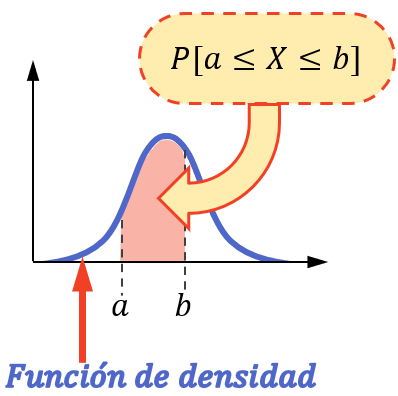
โปรดทราบว่าการคำนวณความน่าจะเป็นสามารถทำได้ด้วยวิธีนี้ก็ต่อเมื่อตัวแปรทางสถิติเป็นไปตามการแจกแจงแบบต่อเนื่อง เช่น การแจกแจงแบบปกติ การแจกแจงแบบเอ็กซ์โปเนนเชียล การแจกแจงแบบปัวซอง เป็นต้น

คุณสมบัติของฟังก์ชันความหนาแน่น

ฟังก์ชันความหนาแน่นมีคุณสมบัติดังต่อไปนี้:

ค่าของฟังก์ชันความหนาแน่นเป็นศูนย์หรือบวกสำหรับค่าใดๆ ของ x

$f(x)\geq 0$

นอกจากนี้ ค่าสูงสุดของฟังก์ชันความหนาแน่นจะเท่ากับ 1

$f(x)\leq 1$

ในความเป็นจริง พื้นที่ทั้งหมดใต้กราฟฟังก์ชันความหนาแน่นจะเท่ากับ 1 เสมอโดยไม่คำนึงถึงตัวแปร เนื่องจากมันสอดคล้องกับเซตของความน่าจะเป็นทั้งหมด

$\displaystyle \int_{-\infty}^{+\infty} f(x)dx=1$

ตามที่อธิบายไว้ในส่วนที่แล้ว ความน่าจะเป็นที่ตัวแปรต่อเนื่องรับค่าในช่วงเวลาหนึ่งจะคำนวณด้วยอินทิกรัลของฟังก์ชันความหนาแน่นในช่วงเวลานั้น

$\displaystyle P[a\leq X\leq b]=\int_a^b f(x)dx=F(b)-F(a)$

ฟังก์ชันความหนาแน่นและฟังก์ชันการกระจาย

ในส่วนสุดท้ายนี้ เราจะดูว่าฟังก์ชันความหนาแน่นและฟังก์ชันการแจกแจงแตกต่างกันอย่างไร เนื่องจากเป็นฟังก์ชันความน่าจะเป็นสองประเภทที่โดยทั่วไปแล้วจะสับสน

ในทางคณิตศาสตร์ ฟังก์ชันการแจกแจงเทียบเท่ากับอินทิกรัลของฟังก์ชันความหนาแน่น ดังนั้นฟังก์ชันการแจกแจงจึงอธิบายความน่าจะเป็นสะสมของตัวแปรต่อเนื่อง

นั่นคือ รูปภาพของฟังก์ชันการแจกแจงสำหรับค่าใดๆ จะเท่ากับความน่าจะเป็นที่ตัวแปรจะใช้ค่านั้นหรือค่าที่ต่ำกว่า

ความสัมพันธ์ทางคณิตศาสตร์ระหว่างฟังก์ชันทั้งสองประเภทนี้จึงเป็นดังนี้:

$\displaystyle P[X\leq a]=\int_{-\infty}^a f(x)dx=F(a)$

ทอง

$f(x)$

คือฟังก์ชันความหนาแน่น และ

$F(x)$

คือฟังก์ชันการกระจาย

สังเกตว่าการแสดงกราฟความหนาแน่นของฟังก์ชันความหนาแน่นเปลี่ยนแปลงอย่างไรโดยสัมพันธ์กับฟังก์ชันการกระจายของตัวแปรที่ตามหลังการแจกแจงแบบปกติด้วยค่าเฉลี่ย 1 และค่าเบี่ยงเบนมาตรฐาน 0.5:

ความแตกต่างระหว่างฟังก์ชันการกระจายและฟังก์ชันความหนาแน่น

หากต้องการเรียนรู้เพิ่มเติมเกี่ยวกับคุณลักษณะการเผยแพร่ คลิกลิงก์ด้านล่าง:

➤ ดูที่: ฟังก์ชันการกระจาย

เกี่ยวกับผู้แต่ง

ดร.เบนจามิน แอนเดอร์สัน

สวัสดี ฉันชื่อเบนจามิน ศาสตราจารย์สถิติเกษียณอายุแล้ว และผันตัวมาเป็นครูสอนสถิติโดยเฉพาะ ด้วยประสบการณ์และความเชี่ยวชาญที่กว้างขวางในสาขาสถิติ ฉันกระตือรือร้นที่จะแบ่งปันความรู้ของฉันเพื่อเสริมศักยภาพนักเรียนผ่าน Statorials. รู้เพิ่มเติม