ฟังก์ชันการกระจาย

โดย ดร.เบนจามิน แอนเดอร์สัน สิงหาคม 5, 2023 ความน่าจะเป็น 0 ความคิดเห็น

ในบทความนี้ คุณจะพบคำอธิบายเกี่ยวกับฟังก์ชันการแจกแจง วิธีคำนวณค่าของมัน และตัวอย่างฟังก์ชันการแจกแจงในโลกแห่งความเป็นจริง นอกจากนี้ คุณจะเห็นความแตกต่างระหว่างฟังก์ชันการกระจายและฟังก์ชันความหนาแน่นได้

ฟังก์ชันการกระจายคืออะไร?

ฟังก์ชันการแจกแจง หรือที่เรียกว่า ฟังก์ชันการแจกแจงสะสม เป็นฟังก์ชันทางคณิตศาสตร์ที่บ่งชี้ความน่าจะเป็นสะสมของการแจกแจง นั่นคือ รูปภาพของฟังก์ชันการแจกแจงสำหรับค่าใดๆ จะเท่ากับความน่าจะเป็นที่ตัวแปรจะใช้ค่านั้นหรือค่าที่ต่ำกว่า

ฟังก์ชันการแจกแจงสะสมอาจเรียกโดยตัวย่อ FDA แม้ว่าสัญลักษณ์ตามปกติของฟังก์ชันจะเป็นตัวพิมพ์ใหญ่ F

ฟังก์ชันการกระจายจึงถูกกำหนดโดยสูตรต่อไปนี้:

$F(x)=P[X\leq x]$

วิธีการคำนวณฟังก์ชันการกระจาย

จากนั้นเราจะอธิบายวิธีคำนวณค่าของฟังก์ชันการแจกแจง โดยขึ้นอยู่กับว่าการแจกแจงความน่าจะเป็นเป็นแบบแยกส่วนหรือต่อเนื่องกัน

กล่องรอบคอบ

หากตัวแปรสุ่มไม่ต่อเนื่อง ฟังก์ชันการแจกแจงสะสมจะเท่ากับผลรวมของความน่าจะเป็นของค่าทั้งหมดเท่ากับหรือน้อยกว่า x

$\displaystyle F(x)=P[X\leq x]=\sum_{u\leq x}f(u)$

ทอง

$f(u)$

คือฟังก์ชันความน่าจะเป็นที่เกี่ยวข้องกับตัวแปรไม่ต่อเนื่อง

คดีต่อเนื่อง

หากตัวแปรสุ่มมีความต่อเนื่อง ฟังก์ชันการแจกแจงสะสมจะเทียบเท่ากับอินทิกรัลของฟังก์ชันความหนาแน่นตั้งแต่ลบอนันต์ไปจนถึงค่าที่ต้องการ

$\displaystyle F(x)=P[X\leq x]=\int_{-\infty}^{x}f(u)du$

ทอง

$f(u)$

คือฟังก์ชันความหนาแน่นที่เกี่ยวข้องกับตัวแปรต่อเนื่อง

ตัวอย่างฟังก์ชันการกระจาย

ตอนนี้เรารู้คำจำกัดความของฟังก์ชันการแจกแจงแล้ว เรามาดูตัวอย่างเชิงปฏิบัติทีละขั้นตอนเพื่อเรียนรู้วิธีคำนวณค่าฟังก์ชันการแจกแจงกัน

คำนวณฟังก์ชันการแจกแจงสำหรับการทดลองสุ่มการโยนเหรียญสี่ครั้ง

ในการแก้ปัญหาแบบฝึกหัด ก่อนอื่นคุณต้องคำนวณความน่าจะเป็นทั้งหมดที่เกี่ยวข้องกับจำนวนหัวที่ได้รับระหว่างการโยนเหรียญทั้งสี่ครั้ง:

ดังนั้น เนื่องจากเป็นตัวแปรที่ไม่ต่อเนื่อง ในการกำหนดภาพของฟังก์ชันการแจกแจง จึงเพียงพอที่จะเพิ่มความน่าจะเป็นจนถึงค่าของตัวแปรที่ต้องการ:

$\begin{array}{l}F(X\leq 0)=f(0)=0,0625\\[4ex]\begin{aligned}F(X\leq 1)& =f(0)+f(1)\\[1.1ex] & =0,0625+0,25=0,3125\end{aligned}\\[6ex]\begin{aligned}F(X\leq 2)& =f(0)+f(1)+f(2)\\[1.1ex] & =0,0625+0,25+0,375=0,6875\end{aligned}\\[6ex]\begin{aligned}F(X\leq 3)& =f(0)+f(1)+f(2)+f(3)\\[1.1ex] & =0,0625+0,25+0,375+0,25=0,9375\end{aligned}\\[6ex]\begin{aligned}F(X\leq 4)& =f(0)+f(1)+f(2)+f(3)+f(4)\\[1.1ex] & =0,0625+0,25+0,375+0,25+0,0625=1\end{aligned}\end{array}$

ดังนั้นค่าของฟังก์ชันการกระจายของการพลิกหัวโดยการโยนเหรียญอิสระสี่เหรียญจึงเป็นดังนี้:

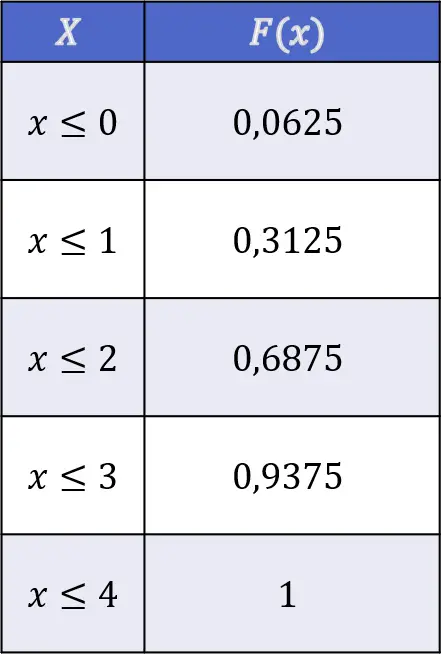
คุณสมบัติของฟังก์ชันการกระจาย

ไม่ว่าตัวแปรชนิดใด ฟังก์ชันการแจกแจงจะมีคุณสมบัติดังต่อไปนี้เสมอ:

ค่าของฟังก์ชันการแจกแจงสะสมอยู่ระหว่าง 0 ถึง 1 รวม

$0\leq F(x) \leq 1$

ลิมิตของฟังก์ชันการกระจายเมื่อ x มีแนวโน้มจะอนันต์เท่ากับ 1

$\displaystyle\lim_{x\to +\infty} F(x)=1$

ในทางกลับกัน ลิมิตของฟังก์ชันการกระจายเมื่อ x เข้าใกล้ลบอนันต์จะเป็นศูนย์

$\displaystyle\lim_{x\to -\infty} F(x)=0$

ตามลักษณะของฟังก์ชันการกระจายจะเป็นแบบโมโนโทนิกและไม่ลดลง

$x_1 \leq x_2 \implies F(x_1)\leq F(x_2)$

นอกจากนี้หาก
$a\leq b$

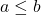
สมการต่อไปนี้เป็นที่พอใจ

 *** QuickLaTeX cannot compile formula:
\begin{array}{l}P(X < a) = F(a^-)\\[2ex] P(X>a)=1-F(a)\\[2ex]P(X \ge a )=1-F(a^-)\\[2ex]P(a<ul><li> Finally, if the statistical variable is continuous, the following equality is satisfied: </li></ul>[latex ]\begin{array}{l}P(a \le X < b) = \displaystyle\int_{a}^{b}f(x)\,dx = F(b)- F(a)\end{array}

*** Error message:
Missing $ inserted.
leading text: \begin{array}{l}
Please use \mathaccent for accents in math mode.
leading text: ... the statistical variable is continuous, the
Please use \mathaccent for accents in math mode.
leading text: ...iable statistic is continuous, equality
\begin{array} on input line 8 ended by \end{document}.
leading text: \end{document}
Improper \prevdepth.
leading text: \end{document}
Missing $ inserted.
leading text: \end{document}
Missing } inserted.
leading text: \end{document}
Missing \cr inserted.
leading text: \end{document}
Missing $ inserted.
leading text: \end{document}
You can't use `\end' in internal vertical mode.
leading text: \end{document}
\begin{array} on input line 8 ended by \end{document}.
leading text: \end{document}

ฟังก์ชันการกระจายและฟังก์ชันความหนาแน่น

สุดท้ายนี้ เราจะเห็นว่าอะไรคือความแตกต่างระหว่างฟังก์ชันการแจกแจงและฟังก์ชันความหนาแน่น เนื่องจากแนวคิดทางสถิติทั้งสองนี้มักจะสับสน

ความแตกต่างระหว่างฟังก์ชันการแจกแจงและฟังก์ชันความหนาแน่น คือประเภทของความน่าจะเป็นที่ฟังก์ชันดังกล่าวกำหนด ฟังก์ชันความหนาแน่นอธิบายความน่าจะเป็นที่ตัวแปรใช้กับค่าที่กำหนด ในขณะที่ฟังก์ชันการแจกแจงอธิบายความน่าจะเป็นสะสมของตัวแปร

นั่นคือฟังก์ชันการแจกแจงใช้ในการคำนวณความน่าจะเป็นที่ตัวแปรมีค่าเท่ากับหรือน้อยกว่าค่าที่กำหนด

โปรดทราบว่าฟังก์ชันความหนาแน่นหมายถึงตัวแปรต่อเนื่องเท่านั้น ดังนั้นความแตกต่างนี้จะสมเหตุสมผลหากตัวแปรที่กำลังศึกษาเป็นแบบต่อเนื่องเท่านั้น

สังเกตว่าการแสดงฟังก์ชันการกระจายแบบกราฟิกเปลี่ยนแปลงไปอย่างไรเมื่อเปรียบเทียบกับฟังก์ชันความหนาแน่นของตัวแปรที่ตามหลังการแจกแจงแบบปกติด้วยค่าเฉลี่ย 1 และค่าเบี่ยงเบนมาตรฐาน 0.5:

ความแตกต่างระหว่างฟังก์ชันการกระจายและฟังก์ชันความหนาแน่น

หากต้องการเรียนรู้เพิ่มเติมเกี่ยวกับฟังก์ชันความหนาแน่น โปรดดูบทความต่อไปนี้:

➤ ดูที่: ฟังก์ชันความหนาแน่น

เกี่ยวกับผู้แต่ง

ดร.เบนจามิน แอนเดอร์สัน

สวัสดี ฉันชื่อเบนจามิน ศาสตราจารย์สถิติเกษียณอายุแล้ว และผันตัวมาเป็นครูสอนสถิติโดยเฉพาะ ด้วยประสบการณ์และความเชี่ยวชาญที่กว้างขวางในสาขาสถิติ ฉันกระตือรือร้นที่จะแบ่งปันความรู้ของฉันเพื่อเสริมศักยภาพนักเรียนผ่าน Statorials. รู้เพิ่มเติม