วิธีการดำเนินการถดถอยพหุนามโดยใช้ scikit-learn
การถดถอยพหุนาม เป็นเทคนิคที่เราสามารถใช้ได้เมื่อความสัมพันธ์ระหว่างตัวแปรทำนายและ ตัวแปรตอบสนอง ไม่เป็นเชิงเส้น
การถดถอยประเภทนี้อยู่ในรูปแบบ:
Y = β 0 + β 1 X + β 2 X 2 + … + β ชั่วโมง
โดยที่ h คือ “ดีกรี” ของพหุนาม
ตัวอย่างทีละขั้นตอนต่อไปนี้แสดงวิธีการถดถอยพหุนามใน Python โดยใช้ sklearn
ขั้นตอนที่ 1: สร้างข้อมูล
ขั้นแรก เรามาสร้างอาร์เรย์ NumPy สองตัวเพื่อเก็บค่าของตัวทำนายและตัวแปรตอบสนอง:
import matplotlib. pyplot as plt import numpy as np #define predictor and response variables x = np. array ([2, 3, 4, 5, 6, 7, 7, 8, 9, 11, 12]) y = np. array ([18, 16, 15, 17, 20, 23, 25, 28, 31, 30, 29]) #create scatterplot to visualize relationship between x and y plt. scatter (x,y)
จากแผนภาพกระจาย เราจะเห็นว่าความสัมพันธ์ระหว่าง x และ y ไม่เป็นเชิงเส้น
ดังนั้นจึงเป็นความคิดที่ดีที่จะปรับแบบจำลองการถดถอยพหุนามเข้ากับข้อมูลเพื่อจับความสัมพันธ์แบบไม่เชิงเส้นระหว่างตัวแปรทั้งสอง
ขั้นตอนที่ 2: ติดตั้งแบบจำลองการถดถอยพหุนาม
รหัสต่อไปนี้แสดงวิธีใช้ฟังก์ชัน sklearn เพื่อให้พอดีกับแบบจำลองการถดถอยพหุนามระดับ 3 กับชุดข้อมูลนี้:
from sklearn. preprocessing import PolynomialFeatures
from sklearn. linear_model import LinearRegression
#specify degree of 3 for polynomial regression model
#include bias=False means don't force y-intercept to equal zero
poly = PolynomialFeatures(degree= 3 , include_bias= False )
#reshape data to work properly with sklearn
poly_features = poly. fit_transform ( x.reshape (-1, 1))
#fit polynomial regression model
poly_reg_model = LinearRegression()
poly_reg_model. fit (poly_features,y)
#display model coefficients
print (poly_reg_model. intercept_ , poly_reg_model. coef_ )
33.62640037532282 [-11.83877127 2.25592957 -0.10889554]
การใช้ค่าสัมประสิทธิ์แบบจำลองที่แสดงในแถวสุดท้าย เราสามารถเขียนสมการถดถอยพหุนามแบบพอดีได้ดังนี้:
y = -0.109x 3 + 2.256x 2 – 11.839x + 33.626
สมการนี้สามารถใช้เพื่อค้นหาค่าที่คาดหวังของตัวแปรตอบสนองโดยให้ค่าที่กำหนดของตัวแปรทำนาย
ตัวอย่างเช่น ถ้า x คือ 4 ค่าที่คาดหวังสำหรับตัวแปรตอบสนอง y จะเป็น 15.39:
y = -0.109(4) 3 + 2.256(4) 2 – 11.839(4) + 33.626= 15.39
หมายเหตุ : เพื่อให้พอดีกับโมเดลการถดถอยพหุนามที่มีดีกรีที่แตกต่างกัน เพียงเปลี่ยนค่าของอาร์กิวเมนต์ ดีกรี ในฟังก์ชัน PolynomialFeatures()
ขั้นตอนที่ 3: เห็นภาพแบบจำลองการถดถอยพหุนาม
สุดท้ายนี้ เราสามารถสร้างพล็อตง่ายๆ เพื่อให้เห็นภาพแบบจำลองการถดถอยพหุนามที่เหมาะกับจุดข้อมูลดั้งเดิม:
#use model to make predictions on response variable
y_predicted = poly_reg_model. predict (poly_features)
#create scatterplot of x vs. y
plt. scatter (x,y)
#add line to show fitted polynomial regression model
plt. plot (x,y_predicted,color=' purple ')
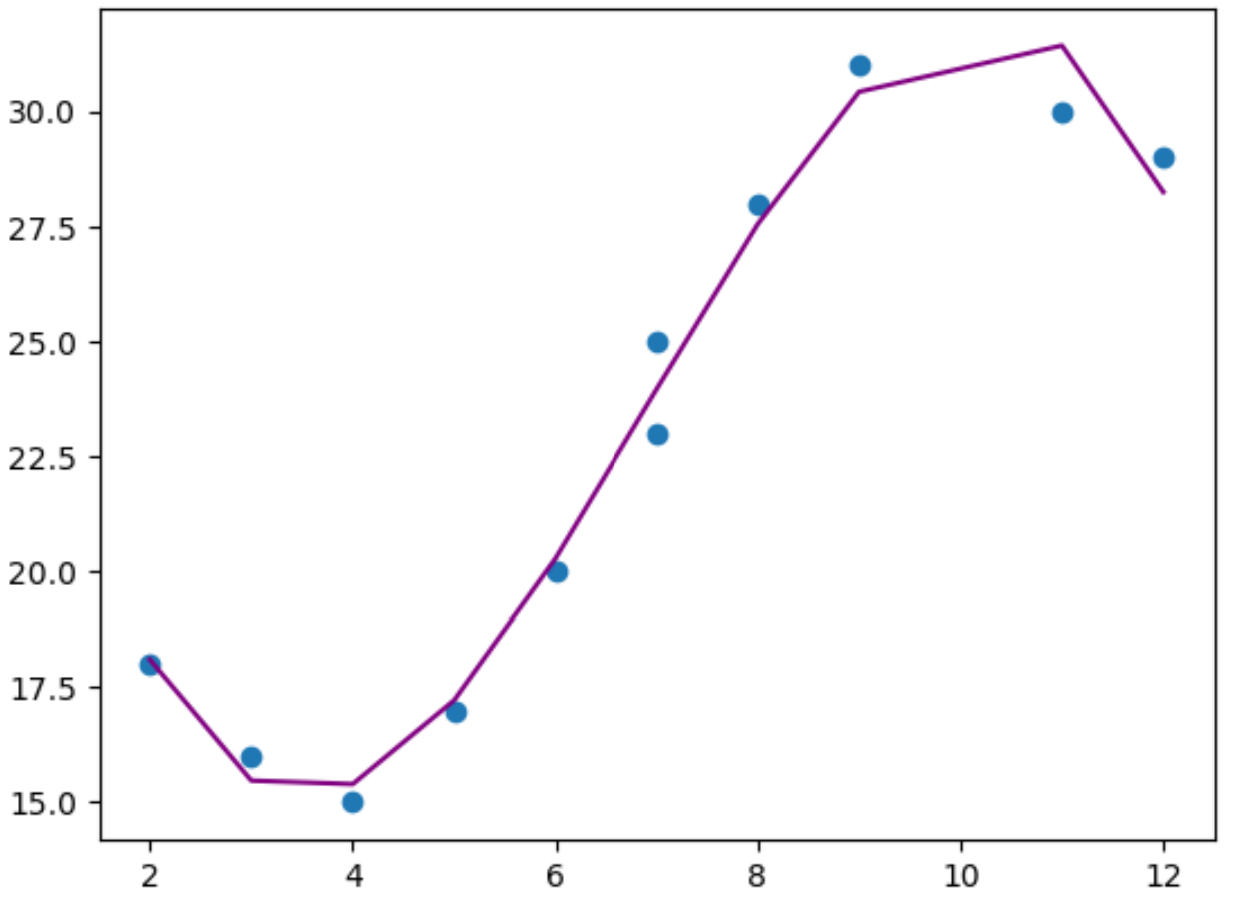
จากกราฟ เราจะเห็นว่าแบบจำลองการถดถอยพหุนามดูเหมือนว่าจะเหมาะสมกับข้อมูลได้ดีโดยไม่ ต้องใส่มากเกินไป
หมายเหตุ : คุณสามารถดูเอกสารฉบับเต็มสำหรับฟังก์ชัน sklearn PolynomialFeatures() ได้ที่นี่
แหล่งข้อมูลเพิ่มเติม
บทช่วยสอนต่อไปนี้จะอธิบายวิธีดำเนินการงานทั่วไปอื่นๆ โดยใช้ sklearn:
วิธีแยกค่าสัมประสิทธิ์การถดถอยจาก sklearn
วิธีการคำนวณความแม่นยำที่สมดุลโดยใช้ sklearn
วิธีตีความรายงานการจำแนกประเภทใน Sklearn