วิธีการตีความข้อผิดพลาดรูทค่าเฉลี่ยกำลังสอง (rmse)
การวิเคราะห์การถดถอย เป็นเทคนิคที่เราสามารถใช้เพื่อทำความเข้าใจความสัมพันธ์ระหว่างตัวแปรทำนายตั้งแต่หนึ่งตัวขึ้นไปและ ตัวแปรตอบสนอง
วิธีหนึ่งในการประเมินว่าแบบจำลองการถดถอยเหมาะสมกับชุดข้อมูลได้ดีเพียงใดคือการคำนวณ ค่าคลาดเคลื่อนกำลังสองเฉลี่ย ซึ่งเป็นหน่วยเมตริกที่บอกเราถึงระยะห่างเฉลี่ยระหว่างค่าที่คาดการณ์ของแบบจำลองกับค่าจริงของชุดข้อมูล
ยิ่ง RMSE ต่ำเท่าไร โมเดลที่กำหนดก็จะสามารถ “พอดี” ชุดข้อมูลได้ดีขึ้นเท่านั้น
สูตรการหาค่าคลาดเคลื่อนกำลังสองเฉลี่ย ซึ่งมักเรียกสั้น ๆ ว่า RMSE คือ:
RMSE = √ Σ(พี i – O i ) 2 / n
ทอง:
- Σ เป็นสัญลักษณ์แฟนซีที่หมายถึง “ผลรวม”
- P i คือค่าที่ทำนายไว้สำหรับการสังเกต ครั้งที่ 3 ในชุดข้อมูล
- O i คือค่าที่สังเกตได้สำหรับการสังเกต ครั้งที่ 3 ในชุดข้อมูล
- n คือขนาดตัวอย่าง
ตัวอย่างต่อไปนี้แสดงวิธีตีความ RMSE สำหรับแบบจำลองการถดถอยที่กำหนด
ตัวอย่าง: วิธีการตีความ RMSE สำหรับแบบจำลองการถดถอย
สมมติว่าเราต้องการสร้างแบบจำลองการถดถอยที่ใช้ “ชั่วโมงเรียน” เพื่อทำนาย “คะแนนสอบ” ของนักเรียนในการสอบเข้าวิทยาลัยโดยเฉพาะ
เรารวบรวมข้อมูลต่อไปนี้สำหรับนักเรียน 15 คน:
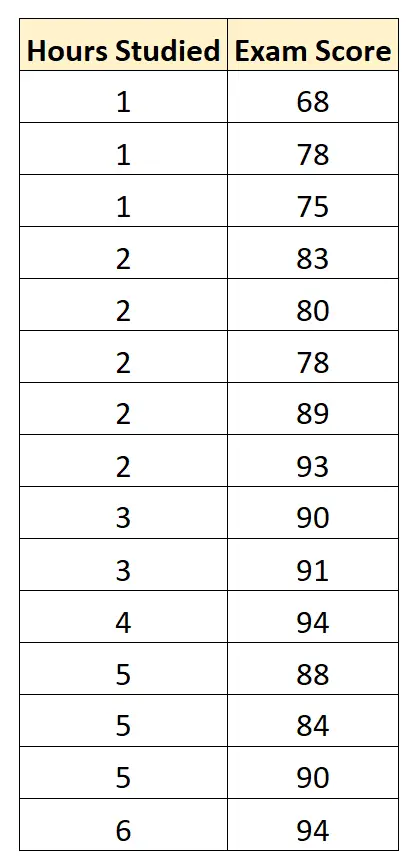
จากนั้นเราใช้ซอฟต์แวร์ทางสถิติ (เช่น Excel, SPSS, R, Python) เป็นต้น เพื่อค้นหาโมเดลการถดถอยที่พอดีต่อไปนี้:
คะแนนสอบ = 75.95 + 3.08* (จำนวนชั่วโมงเรียน)
จากนั้นเราสามารถใช้สมการนี้เพื่อทำนายคะแนนสอบของนักเรียนแต่ละคน โดยพิจารณาจากจำนวนชั่วโมงที่เรียน:
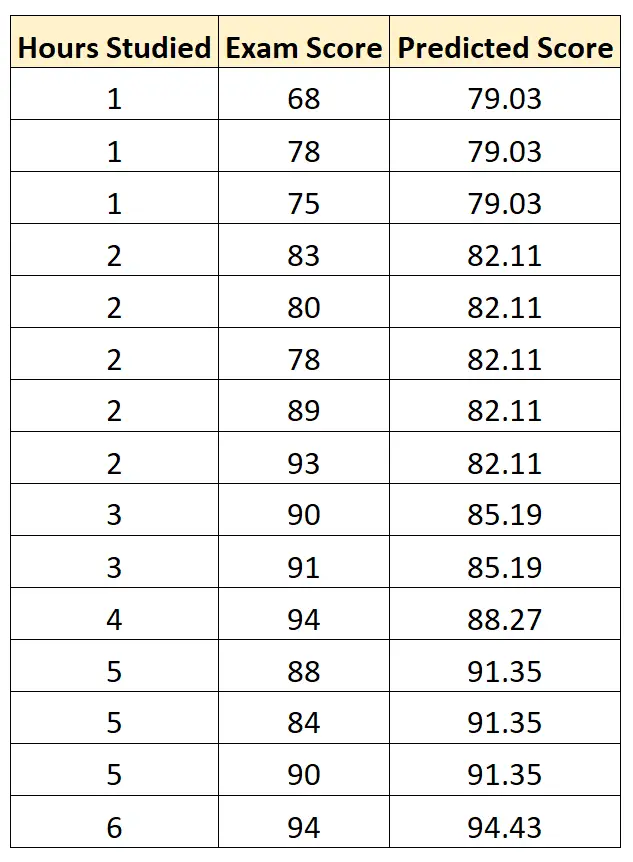
จากนั้นเราสามารถคำนวณผลต่างกำลังสองระหว่างคะแนนสอบที่คาดการณ์ไว้แต่ละคะแนนกับคะแนนสอบจริงได้ จากนั้นเราก็หารากที่สองของค่าเฉลี่ยของผลต่างเหล่านี้ได้:
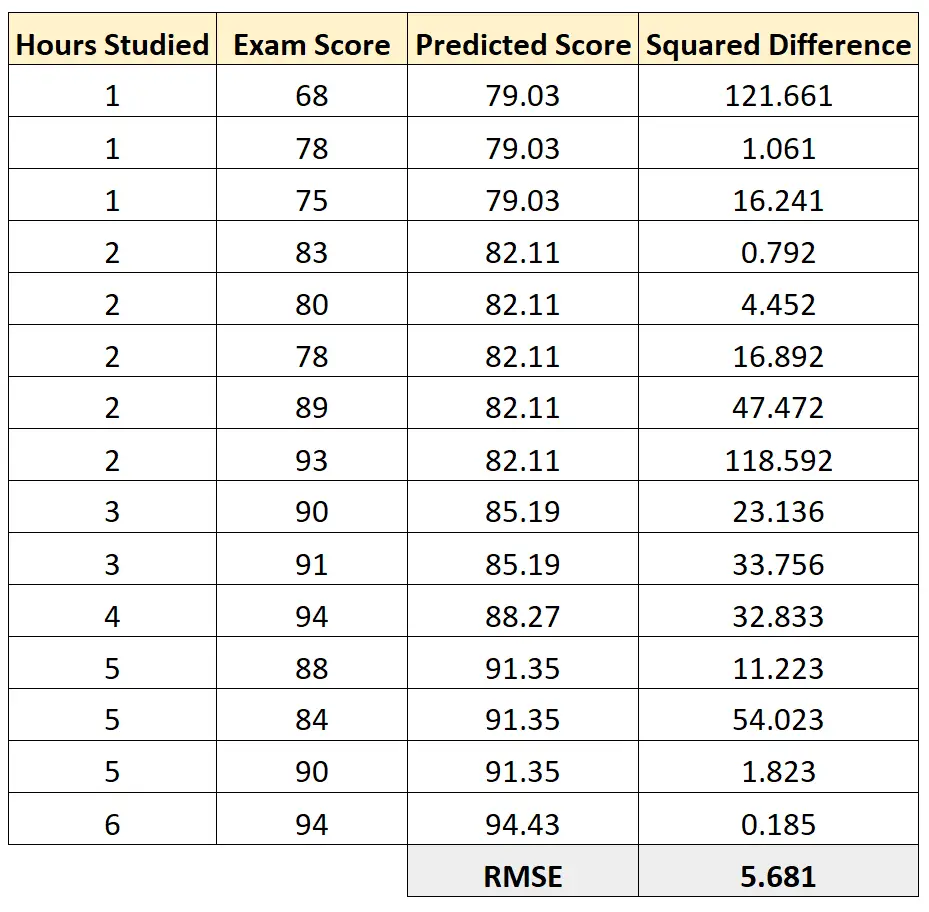
RMSE ของแบบจำลองการถดถอยนี้กลายเป็น 5.681
โปรดจำไว้ว่า ส่วนที่เหลือ ของแบบจำลองการถดถอยคือความแตกต่างระหว่างค่าข้อมูลที่สังเกตได้และค่าที่คาดการณ์ไว้ของแบบจำลอง
คงเหลือ = (P ผม – O ผม )
ทอง
- P i คือค่าที่ทำนายไว้สำหรับการสังเกต ครั้งที่ 3 ในชุดข้อมูล
- O i คือค่าที่สังเกตได้สำหรับการสังเกต ครั้งที่ 3 ในชุดข้อมูล
และโปรดจำไว้ว่า RMSE ของแบบจำลองการถดถอยมีการคำนวณดังนี้:
RMSE = √ Σ(พี i – O i ) 2 / n
ซึ่งหมายความว่า RMSE แสดงถึงรากที่สองของความแปรปรวนของค่าคงเหลือ
นี่เป็นค่าที่มีประโยชน์ที่ควรรู้เพราะมันทำให้เราทราบถึงระยะห่างเฉลี่ยระหว่างค่าข้อมูลที่สังเกตได้กับค่าข้อมูลที่คาดการณ์ไว้
สิ่งนี้ตรงกันข้ามกับ R-squared ของโมเดล ซึ่งบอกเราว่าตัวแปรทำนายของโมเดลสามารถอธิบายความแปรปรวนได้มากเพียงใด
การเปรียบเทียบค่า RMSE ของรุ่นต่างๆ
RMSE มีประโยชน์อย่างยิ่งสำหรับการเปรียบเทียบความพอดีของแบบจำลองการถดถอยต่างๆ
ตัวอย่างเช่น สมมติว่าเราต้องการสร้างแบบจำลองการถดถอยเพื่อทำนายคะแนนสอบของนักเรียน และเราต้องการค้นหาแบบจำลองที่ดีที่สุดที่เป็นไปได้จากแบบจำลองที่เป็นไปได้หลายแบบ
สมมติว่าเราพอดีกับแบบจำลองการถดถอยที่แตกต่างกันสามแบบและค้นหาค่า RMSE ที่สอดคล้องกัน:
- RMSE ของรุ่น 1: 14.5
- RMSE ของโมเดล 2: 16.7
- RMSE ของรุ่น 3: 9.8
โมเดล 3 มี RMSE ต่ำที่สุด ซึ่งบอกเราว่าสามารถใส่ชุดข้อมูลได้ดีที่สุดในบรรดาโมเดลที่เป็นไปได้ทั้งสามแบบ
แหล่งข้อมูลเพิ่มเติม
เครื่องคิดเลข RMSE
วิธีการคำนวณ RMSE ใน Excel
วิธีการคำนวณ RMSE ใน R
วิธีการคำนวณ RMSE ใน Python