วิธีทำการทดสอบ mann-whitney u ใน excel

การทดสอบ Mann-Whitney U (บางครั้งเรียกว่าการทดสอบผลรวมอันดับของ Wilcoxon) ใช้เพื่อเปรียบเทียบความแตกต่างระหว่างสองตัวอย่าง เมื่อการแจกแจงตัวอย่างไม่กระจายตามปกติและขนาดตัวอย่างมีขนาดเล็ก (n < 30)

ถือว่าเทียบเท่าแบบไม่มีพารามิเตอร์ของ การทดสอบ t สองตัวอย่าง

บทช่วยสอนนี้จะอธิบายวิธีดำเนินการทดสอบ Mann-Whitney U ใน Excel

ตัวอย่าง: การทดสอบ Mann-Whitney U ใน Excel

นักวิจัยต้องการทราบว่าการบำบัดน้ำมันเชื้อเพลิงทำให้ MPG เฉลี่ยของรถยนต์เปลี่ยนแปลงหรือไม่ เพื่อทดสอบสิ่งนี้ พวกเขาทำการทดลองโดยวัด MPG ของรถยนต์ 12 คันที่มีการบำบัดน้ำมันเชื้อเพลิง และ 12 คันที่ไม่มีการบำบัด

เนื่องจากขนาดตัวอย่างมีขนาดเล็กและพวกเขาสงสัยว่าการแจกแจงตัวอย่างไม่ปกติกระจาย พวกเขาจึงตัดสินใจทำการทดสอบ Mann-Whitney U เพื่อตรวจสอบว่ามีความแตกต่างที่มีนัยสำคัญทางสถิติใน mpg ระหว่างทั้งสองกลุ่มหรือไม่

ทำตามขั้นตอนต่อไปนี้เพื่อทำการทดสอบ Mann-Whitney U ใน Excel

ขั้นตอนที่ 1: ป้อนข้อมูล

ป้อนข้อมูลดังต่อไปนี้:

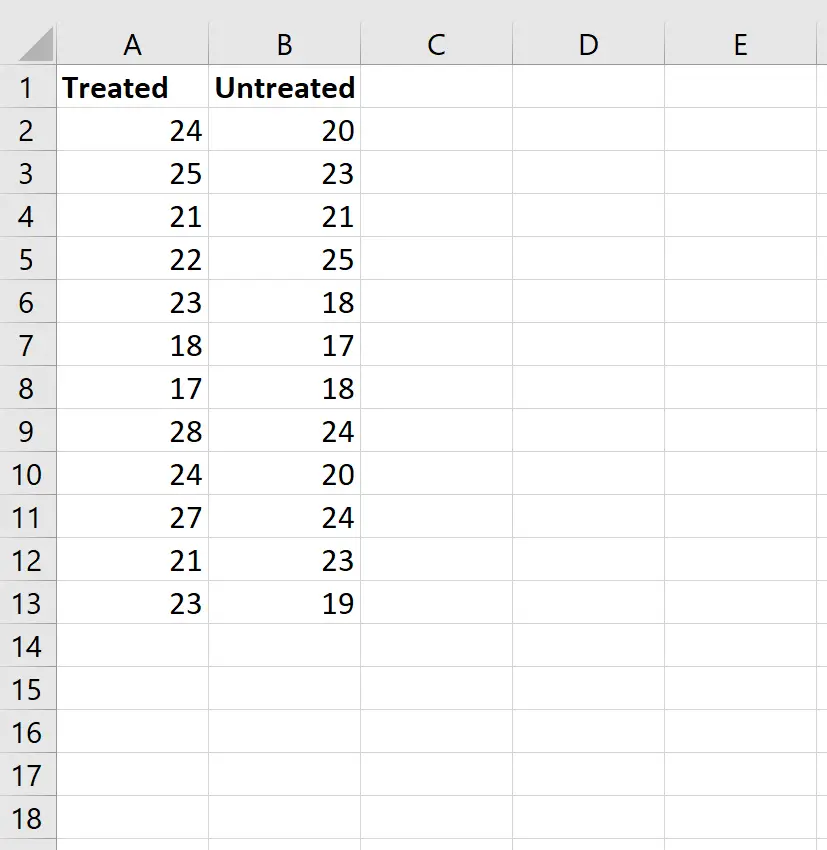
ขั้นตอนที่ 2: คำนวณอันดับของทั้งสองกลุ่ม

ต่อไปเราจะคำนวณอันดับของแต่ละกลุ่ม รูปภาพต่อไปนี้แสดงสูตรที่จะใช้คำนวณอันดับของค่าแรกในกลุ่มที่ประมวลผลแล้ว:

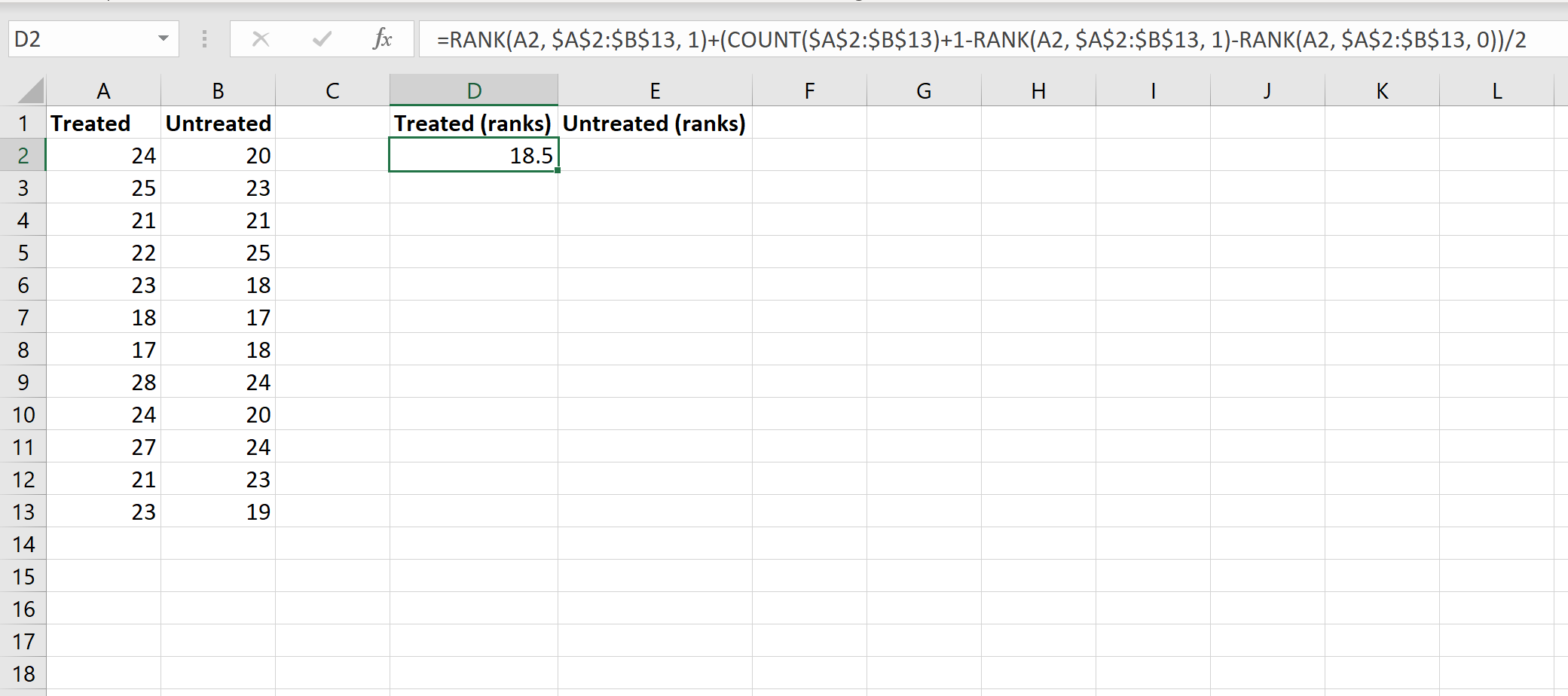
แม้ว่าสูตรนี้จะค่อนข้างซับซ้อน แต่คุณจะต้องป้อนเพียงครั้งเดียวเท่านั้น จากนั้นคุณก็สามารถลากสูตรไปยังเซลล์อื่นๆ ทั้งหมดเพื่อเติมแถวได้:

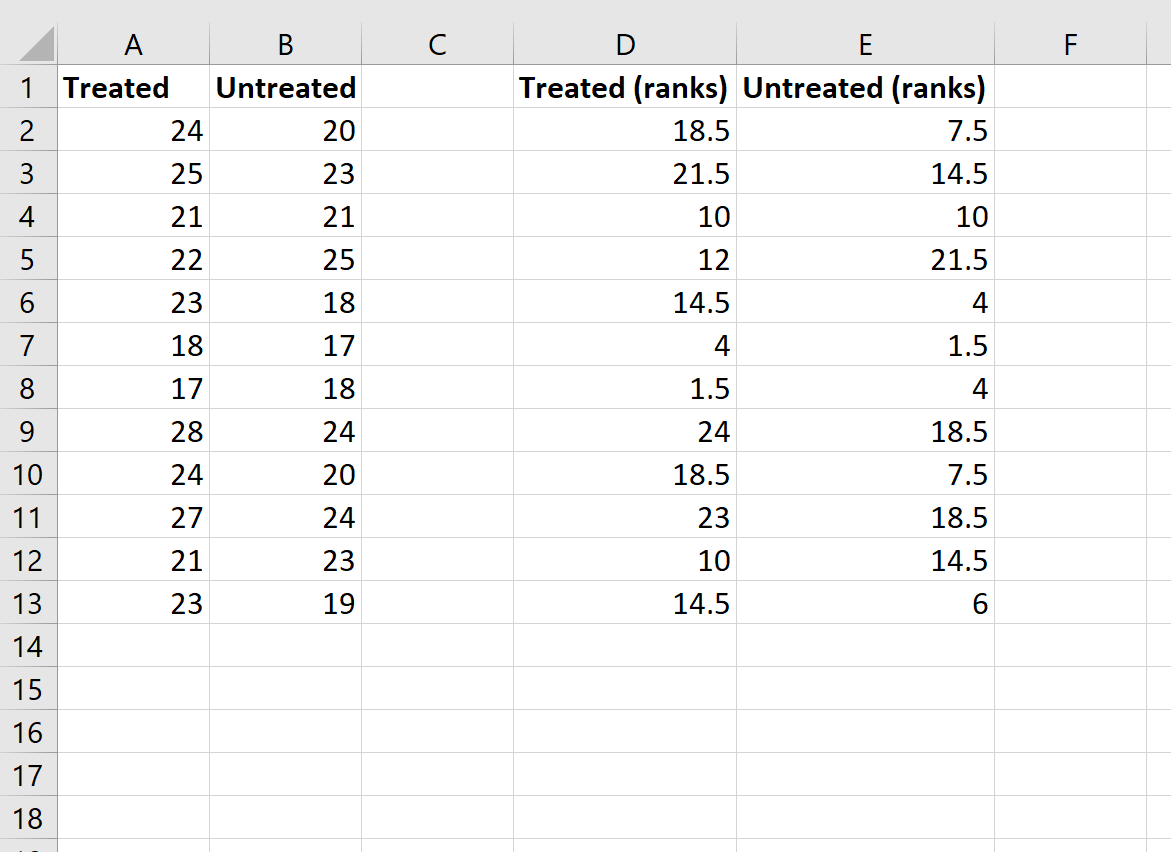
ขั้นตอนที่ 3: คำนวณค่าที่จำเป็นสำหรับสถิติการทดสอบ

ต่อไป เราจะใช้สูตรต่อไปนี้ในการคำนวณผลรวมของอันดับสำหรับแต่ละกลุ่ม ขนาดตัวอย่างสำหรับแต่ละกลุ่ม สถิติการทดสอบ U สำหรับแต่ละกลุ่ม และสถิติการทดสอบ U โดยรวม:

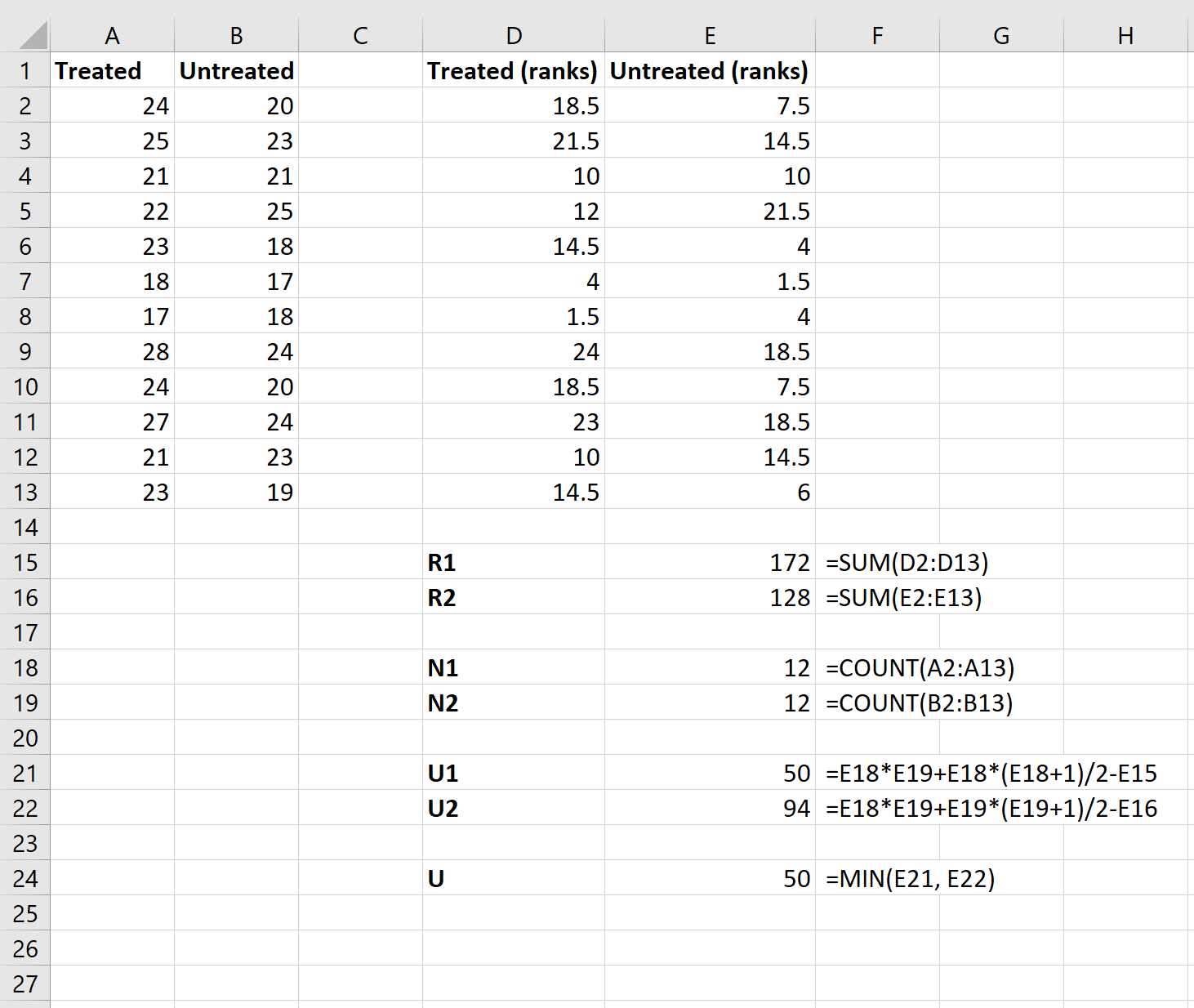
ขั้นตอนที่ 4: คำนวณสถิติการทดสอบ z และค่า p ที่สอดคล้องกัน

สุดท้าย เราจะใช้สูตรต่อไปนี้ในการคำนวณสถิติการทดสอบค่ามาตรฐานและ ค่า p ที่สอดคล้องกันเพื่อพิจารณาว่าเราควรปฏิเสธสมมติฐานว่างหรือไม่:

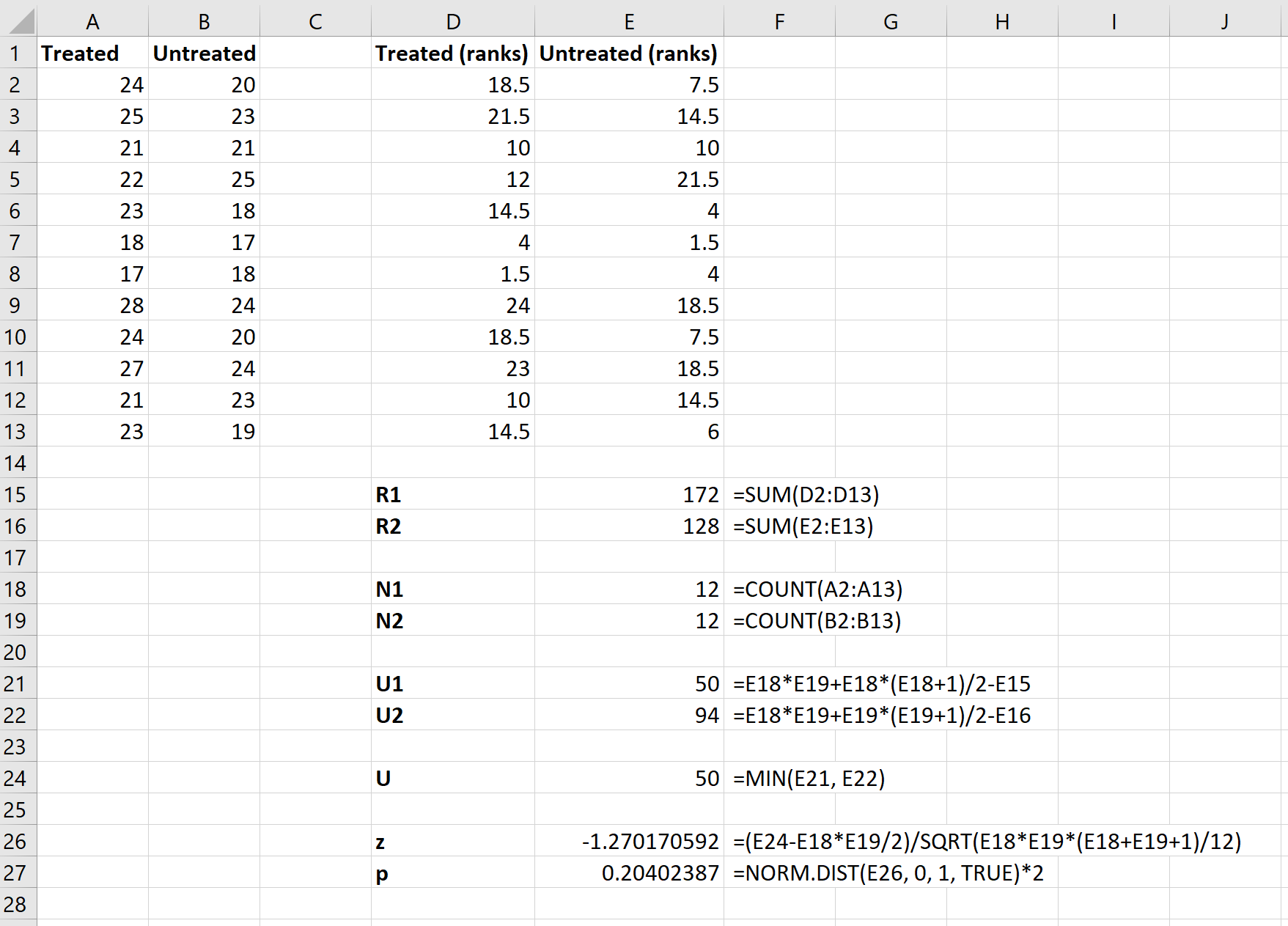
สมมติฐานว่างของการทดสอบระบุว่าทั้งสองกลุ่มมี MPG เฉลี่ยเท่ากัน เนื่องจากค่า p ทดสอบ ( 0.20402387 ) ไม่น้อยกว่าระดับนัยสำคัญของเราที่ 0.05 เราจึงล้มเหลวในการปฏิเสธสมมติฐานว่าง

เราไม่มีหลักฐานเพียงพอที่จะบอกว่า mpg เฉลี่ยที่แท้จริงนั้นแตกต่างกันระหว่างทั้งสองกลุ่ม