วิธีค้นหาค่า p จากคะแนน z ใน excel

การทดสอบสมมติฐาน หลายๆ รายการในสถิติจะส่งผลให้เกิดสถิติการทดสอบ z เมื่อเราพบสถิติการทดสอบค่ามาตรฐานแล้ว เราก็มักจะพบค่า p ที่เกี่ยวข้องด้วย หากค่า p นี้ต่ำกว่าระดับอัลฟ่าที่กำหนด (เช่น 0.10, 0.05, 0.01) เราจะปฏิเสธสมมติฐานว่างของการทดสอบและสรุปว่าผลลัพธ์ของเรามีนัยสำคัญ

บทช่วยสอนนี้สาธิตตัวอย่างต่างๆ ของการค้นหาค่า p จากคะแนน z ใน Excel โดยใช้ฟังก์ชัน NORM.DIST ซึ่งรับอาร์กิวเมนต์ต่อไปนี้:

NORM.DIST (x, ค่าเฉลี่ย, standard_dev, สะสม)

ทอง:

• x คือคะแนน z ที่เราสนใจ
• ค่าเฉลี่ย คือค่าเฉลี่ยของการแจกแจง เราจะใช้ “0” สำหรับการแจกแจงแบบปกติมาตรฐาน
• standard_dev คือค่าเบี่ยงเบนมาตรฐานของการแจกแจง เราจะใช้ “1” สำหรับการแจกแจงแบบปกติมาตรฐาน
• cumulative รับค่า “TRUE” (ส่งคืน CDF) หรือ “FALSE” (ส่งคืน PDF) – เราจะใช้ “TRUE” เพื่อรับค่าของฟังก์ชันการแจกแจงสะสม

เรามาดูตัวอย่างกัน

ตัวอย่างที่ 1: การค้นหาค่า P จากคะแนน Z (การทดสอบแบบสองด้าน)

บริษัทต้องการทราบว่าแบตเตอรี่ชนิดใหม่มีอายุการใช้งานเฉลี่ยแตกต่างจากแบตเตอรี่มาตรฐานปัจจุบันซึ่งมีอายุการใช้งานเฉลี่ย 18 ชั่วโมงหรือไม่ ใน การสุ่มตัวอย่าง แบตเตอรี่ใหม่ 100 ก้อน พวกเขาพบว่าอายุการใช้งานเฉลี่ยคือ 19 ชั่วโมง โดยมีค่าเบี่ยงเบนมาตรฐาน 4 ชั่วโมง

ทำการทดสอบสมมติฐานแบบสองด้านโดยใช้ระดับอัลฟา 0.05 เพื่อตรวจสอบว่าอายุการใช้งานเฉลี่ยของแบตเตอรี่ใหม่แตกต่างจากอายุการใช้งานเฉลี่ยของแบตเตอรี่มาตรฐานปัจจุบันหรือไม่

ขั้นตอนที่ 1: ระบุ สมมติฐาน

สมมติฐานว่าง (H ₀ ): μ = 18

สมมติฐานทางเลือก: (ฮา): μ ≠ 18

ขั้นตอนที่ 2: ค้นหาสถิติการทดสอบ z

สถิติการทดสอบ z = (x-μ) / (s/√n) = (19-18) / (4/√100) = 2.5

ขั้นตอนที่ 3: ค้นหาค่า p ของสถิติการทดสอบ z โดยใช้ Excel

หากต้องการค้นหาค่า p สำหรับ z = 2.5 เราจะใช้สูตรต่อไปนี้ใน Excel: =1 – NORM.DIST(2.5, 0, 1, TRUE)

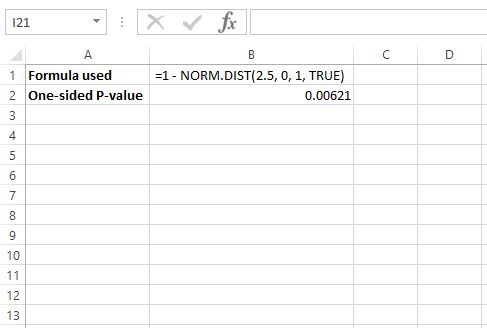
นี่บอกเราว่าค่า p ด้านเดียวคือ .00621 แต่เนื่องจากเรากำลังทำการทดสอบแบบสองด้าน เราจึงต้องคูณค่านี้ด้วย 2 ดังนั้นค่า p จะเป็น .00612 * 2 = .01224

ขั้นตอนที่ 4: ปฏิเสธหรือไม่ปฏิเสธสมมติฐานว่าง

เนื่องจากค่า p ของ 0.01224 น้อยกว่าระดับอัลฟาที่เลือกคือ 0.05 เราจึงปฏิเสธสมมติฐานที่เป็นโมฆะ เรามีหลักฐานเพียงพอที่จะบอกว่าอายุการใช้งานเฉลี่ยของแบตเตอรี่ใหม่แตกต่างอย่างมากจากอายุการใช้งานเฉลี่ยของแบตเตอรี่มาตรฐานในปัจจุบัน

ตัวอย่างที่ 2: การค้นหาค่า P จากคะแนน Z (การทดสอบด้านเดียว)

นักพฤกษศาสตร์ประเมินว่าความสูงเฉลี่ยของพืชบางชนิดคือน้อยกว่า 14 นิ้ว เธอสุ่มเลือกต้นไม้ 30 ต้นและวัดขนาดพวกมัน เธอพบว่าความสูงเฉลี่ยอยู่ที่ 13.5 นิ้ว โดยมีค่าเบี่ยงเบนมาตรฐาน 2 นิ้ว

ทำการทดสอบสมมติฐานด้านเดียวโดยใช้ระดับอัลฟา 0.01 เพื่อตรวจสอบว่าความสูงเฉลี่ยของต้นไม้นี้น้อยกว่า 14 นิ้วจริงหรือไม่

ขั้นตอนที่ 1: ระบุ สมมติฐาน

สมมติฐานว่าง (H0): μ≥ 14

สมมติฐานทางเลือก: (ฮา): μ < 14

ขั้นตอนที่ 2: ค้นหาสถิติการทดสอบ z

สถิติการทดสอบ z = (x-μ) / (s/√n) = (13.5-14) / (2/√30) = -1.369

ขั้นตอนที่ 3: ค้นหาค่า p ของสถิติการทดสอบ z โดยใช้ Excel

หากต้องการค้นหาค่า p สำหรับ z = -1.369 เราจะใช้สูตรต่อไปนี้ใน Excel: =NORM.DIST(-1.369, 0, 1, TRUE)

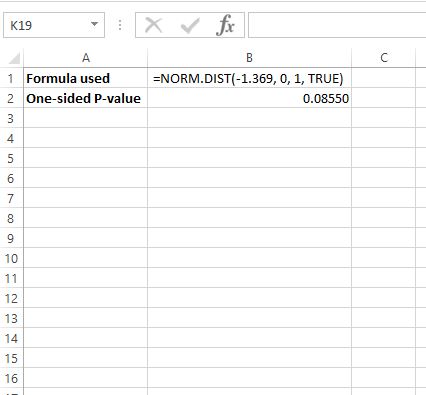
สิ่งนี้บอกเราว่าค่า p ด้านเดียวคือ 0.08550

ขั้นตอนที่ 4: ปฏิเสธหรือไม่ปฏิเสธสมมติฐานว่าง

เนื่องจากค่า p ของ 0.08550 มากกว่าระดับอัลฟาที่เลือกคือ 0.01 เราจึงไม่สามารถปฏิเสธสมมติฐานที่เป็นโมฆะได้ เราไม่มีหลักฐานเพียงพอที่จะบอกว่าความสูงเฉลี่ยของพืชชนิดนี้คือน้อยกว่า 14 นิ้ว

หากต้องการบทช่วยสอน เพิ่มเติม เกี่ยวกับสถิติใน Excel โปรดตรวจดูรายการ คำแนะนำ Excel ทั้งหมดของเรา