วิธีอ่านตารางแจกแจงไคสแควร์

บทช่วยสอนนี้จะอธิบายวิธีการอ่านและตีความแผนภูมิการกระจายไคสแควร์

ตารางการกระจายไคสแควร์คืออะไร?

ตารางการกระจาย ไคสแควร์ เป็นตารางที่แสดงค่าวิกฤตของการแจกแจงไคสแควร์ หากต้องการใช้ตารางการแจกแจงไคสแควร์ คุณจะต้องทราบค่าเพียงสองค่าเท่านั้น:

• องศาอิสระสำหรับการทดสอบไคสแควร์
• ระดับอัลฟาของการทดสอบ (ตัวเลือกทั่วไปคือ 0.01, 0.05 และ 0.10)

รูปภาพต่อไปนี้แสดง 20 แถวแรกของตารางการกระจายไคสแควร์ โดยมีองศาอิสระทางด้านซ้ายของตาราง และระดับอัลฟ่าที่ด้านบนของตาราง:

หมายเหตุ: คุณสามารถดูตารางการแจกแจงไคสแควร์แบบเต็มพร้อมระดับความเป็นอิสระเพิ่มเติมได้ที่นี่

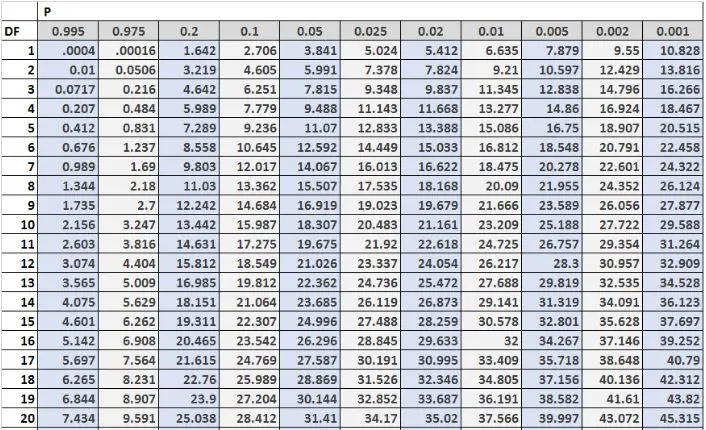
ค่าวิกฤตในตารางมักจะถูกเปรียบเทียบกับสถิติการทดสอบของการทดสอบไคสแควร์ หากสถิติการทดสอบมากกว่าค่าวิกฤตที่พบในตาราง คุณสามารถปฏิเสธสมมติฐานว่างของการทดสอบไคสแควร์ และสรุปได้ว่าผลการทดสอบมีนัยสำคัญทางสถิติ

ตัวอย่างการใช้ตารางแจกแจงไคสแควร์

เราจะแสดงวิธีใช้ตารางการแจกแจงไคสแควร์กับการทดสอบไคสแควร์สามประเภทต่อไปนี้:

• การทดสอบไคสแควร์เพื่อความเป็นอิสระ
• การทดสอบไคสแควร์เพื่อความพอดี
• การทดสอบไคสแควร์เพื่อความสม่ำเสมอ

การทดสอบไคสแควร์เพื่อความเป็นอิสระ

เราใช้ การทดสอบไคสแควร์เพื่อความเป็นอิสระ เมื่อเราต้องการทดสอบว่ามีความสัมพันธ์ที่มีนัยสำคัญระหว่างตัวแปรหมวดหมู่สองตัวหรือไม่

ตัวอย่าง: สมมติว่าเราต้องการทราบว่าเพศสัมพันธ์กับการเลือกพรรคการเมืองหรือไม่ เราสุ่มตัวอย่างผู้มีสิทธิเลือกตั้ง 500 คน และถามพวกเขาเกี่ยวกับความชอบพรรคการเมืองของพวกเขา เราใช้ระดับนัยสำคัญที่ 0.05 เราทำการทดสอบไคสแควร์เพื่อตรวจสอบว่าเพศสัมพันธ์กับความชอบของพรรคการเมืองหรือไม่ ตารางต่อไปนี้แสดงผลการสำรวจ:

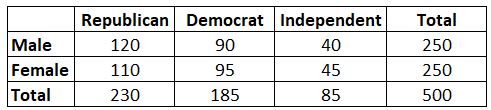
ปรากฎว่าสถิติการทดสอบสำหรับการทดสอบไคสแควร์นี้คือ 0.864

จากนั้นเราจะหาค่าทดสอบวิกฤติในตารางการแจกแจงไคสแควร์ องศาความเป็นอิสระเท่ากับ (#rows-1) * (#columns-1) = (2-1) * (3-1) = 2 และปัญหาบอกเราว่าเราควรใช้ระดับอัลฟา 0.05 ดังนั้น ตามตารางการกระจายไคสแควร์ ค่าวิกฤตของการทดสอบคือ 5.991

เนื่องจากสถิติการทดสอบของเราน้อยกว่าค่าวิกฤติ เราจึงไม่สามารถปฏิเสธสมมติฐานว่างได้ ซึ่งหมายความว่าเราไม่มีหลักฐานเพียงพอที่จะกล่าวว่ามีความสัมพันธ์ระหว่างเพศและการตั้งค่าของพรรคการเมือง

การทดสอบไคสแควร์เพื่อความพอดี

เราใช้ การทดสอบความพอดีของ ไคสแควร์ เมื่อเราต้องการทดสอบว่าตัวแปรเชิงหมวดหมู่เป็นไปตามการแจกแจงเชิงสมมุติหรือไม่

ตัวอย่าง: เจ้าของร้านบอกว่า 30% ของลูกค้าช่วงสุดสัปดาห์มาในวันศุกร์ 50% ในวันเสาร์ และ 20% ในวันอาทิตย์ นักวิจัยอิสระเข้าเยี่ยมชมร้านค้าในช่วงสุดสัปดาห์แบบสุ่มและพบลูกค้า 91 รายในวันศุกร์ 104 รายในวันเสาร์ และ 65 รายในวันอาทิตย์ เราทำการทดสอบไคสแควร์โดยใช้ระดับนัยสำคัญที่ 0.10 เพื่อตรวจสอบความพอดีเพื่อพิจารณาว่าข้อมูลสอดคล้องกับคำกล่าวอ้างของเจ้าของร้านค้าหรือไม่

ในกรณีนี้ สถิติการทดสอบกลายเป็น 10,616

จากนั้นเราจะหาค่าทดสอบวิกฤติในตารางการแจกแจงไคสแควร์ องศาความเป็นอิสระเท่ากับ (#ผลลัพธ์-1) = 3-1 = 2 และปัญหาบอกเราว่าเราควรใช้ระดับอัลฟ่าที่ 0.10 ดังนั้นตามตารางการแจกแจงไคสแควร์ ค่าวิกฤตของการทดสอบคือ 4.605 .

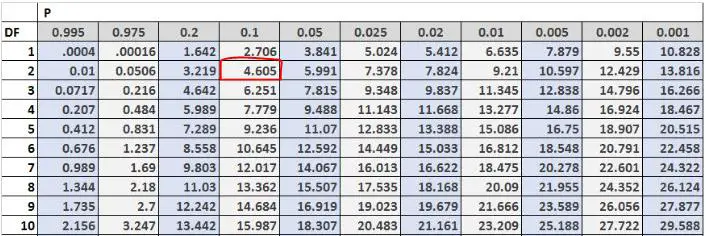
เนื่องจากสถิติการทดสอบของเรามากกว่าค่าวิกฤต เราจึงปฏิเสธสมมติฐานว่าง ซึ่งหมายความว่าเรามีหลักฐานเพียงพอที่จะบอกว่าการกระจายตัวที่แท้จริงของลูกค้าที่มาร้านนี้ในช่วงสุดสัปดาห์ไม่เท่ากับ 30% ในวันศุกร์ 50% ในวันเสาร์ และ 20% ในวันอาทิตย์

การทดสอบไคสแควร์เพื่อความสม่ำเสมอ

เราใช้ การทดสอบไคสแควร์สำหรับความเป็นเนื้อเดียวกัน เมื่อเราต้องการทดสอบอย่างเป็นทางการว่ามีความแตกต่างในสัดส่วนระหว่างหลายกลุ่มหรือไม่

ตัวอย่าง: ศูนย์ฝึกบาสเก็ตบอลแห่งหนึ่งต้องการดูว่าโปรแกรมการฝึกใหม่ 2 รายการปรับปรุงสัดส่วนของผู้เล่นที่ผ่านการทดสอบการยิงที่ยากหรือไม่ ผู้เล่น 172 คนจะถูกสุ่มให้อยู่ในโปรแกรม 1, 173 คนในโปรแกรม 2 และ 215 คนในโปรแกรมปัจจุบัน หลังจากใช้โปรแกรมการฝึกเป็นเวลาหนึ่งเดือน ผู้เล่นจึงทำการทดสอบการยิง ตารางด้านล่างแสดงจำนวนผู้เล่นที่ผ่านการทดสอบการยิงตามโปรแกรมที่พวกเขาใช้

เราทำการทดสอบไคสแควร์โดยใช้ระดับนัยสำคัญที่ 0.05 เพื่อตรวจสอบว่าอัตราความสำเร็จเท่ากันสำหรับแต่ละโปรแกรมการฝึกหรือไม่

ปรากฎว่าสถิติการทดสอบสำหรับการทดสอบไคสแควร์นี้คือ 4.208

จากนั้นเราจะหาค่าทดสอบวิกฤติในตารางการแจกแจงไคสแควร์ องศาความเป็นอิสระเท่ากับ (#rows-1) * (#columns-1) = (2-1) * (3-1) = 2 และปัญหาบอกเราว่าเราควรใช้ระดับอัลฟา 0.05 ดังนั้น ตามตารางการกระจายไคสแควร์ ค่าวิกฤตของการทดสอบคือ 5.991

เนื่องจากสถิติการทดสอบของเราน้อยกว่าค่าวิกฤติ เราจึงไม่สามารถปฏิเสธสมมติฐานว่างได้ ซึ่งหมายความว่าเราไม่มีหลักฐานเพียงพอที่จะกล่าวว่าโปรแกรมการฝึกอบรมทั้งสามโปรแกรมให้ผลลัพธ์ที่แตกต่างกัน