วิธีอ่านตารางการแจกแจงแบบทวินาม

ตารางการแจกแจงแบบทวินาม   เป็นตารางแสดงความน่าจะเป็นที่เกี่ยวข้องกับ การแจกแจงแบบทวินาม หากต้องการใช้ตารางการแจกแจงแบบทวินาม คุณต้องมีค่าเพียง 3 ค่าเท่านั้น:

• n: จำนวนครั้งที่พยายาม
• r: จำนวน “ความสำเร็จ” ระหว่างการพยายาม n ครั้ง
• p: ความน่าจะเป็นที่จะประสบความสำเร็จของการทดลองที่กำหนด

เมื่อใช้ตัวเลขทั้งสามนี้ คุณจะสามารถใช้ตารางการแจกแจงแบบทวินามเพื่อค้นหาความน่าจะเป็นที่จะประสบความสำเร็จ r อย่างแน่นอนตลอดการทดลอง n ครั้ง เมื่อความน่าจะเป็นที่จะประสบความสำเร็จในการทดลองแต่ละครั้งคือ p

ตัวอย่างต่อไปนี้แสดงวิธีการอ่านตารางการแจกแจงแบบทวินาม

ตัวอย่างที่ 1

คำถาม: เจสสิก้าทำ 60% ของความพยายามในการโยนโทษของเธอ ถ้าเธอโยนโทษ 6 ครั้ง ความน่าจะเป็นที่เธอได้โยนโทษ 4 ครั้งพอดีเป็นเท่าใด

เพื่อตอบคำถามนี้ เราสามารถหาค่าในตารางการแจกแจงทวินามที่สอดคล้องกับ n = 6, r = 4 และ p = 0.60:

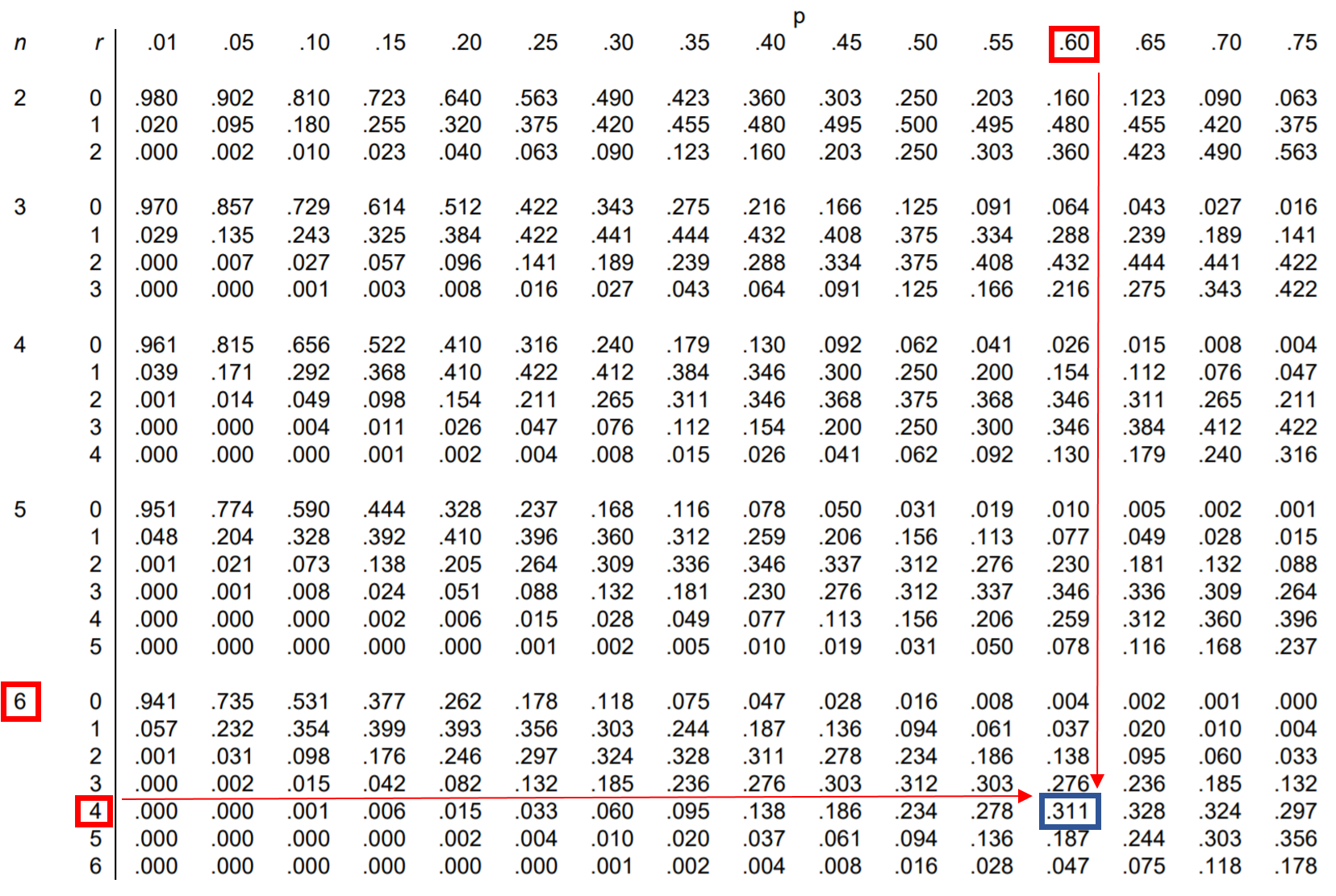
ความน่าจะเป็นที่เจสสิก้าโยนโทษ 4 ครั้งจาก 6 ครั้งพอดีคือ 0.311

ตัวอย่างที่ 2

คำถาม: เจสสิก้าทำ 60% ของความพยายามในการโยนโทษของเธอ ถ้าเธอโยนโทษ 6 ครั้ง ความน่าจะเป็นที่เธอโยนโทษน้อยกว่า 4 ครั้งเป็นเท่าใด

หากต้องการค้นหาความน่าจะเป็นนี้ คุณต้องเพิ่มความน่าจะเป็นต่อไปนี้:

P(ได้น้อยกว่า 4) = P(ได้ 0) + P(ได้ 1) + P(ได้ 2) + P(ได้ 3)

ดังนั้นเราจึงสามารถค้นหาความน่าจะเป็นทั้งสี่ประการเหล่านี้ในตารางการแจกแจงแบบทวินามแล้วบวกเข้าด้วยกัน:

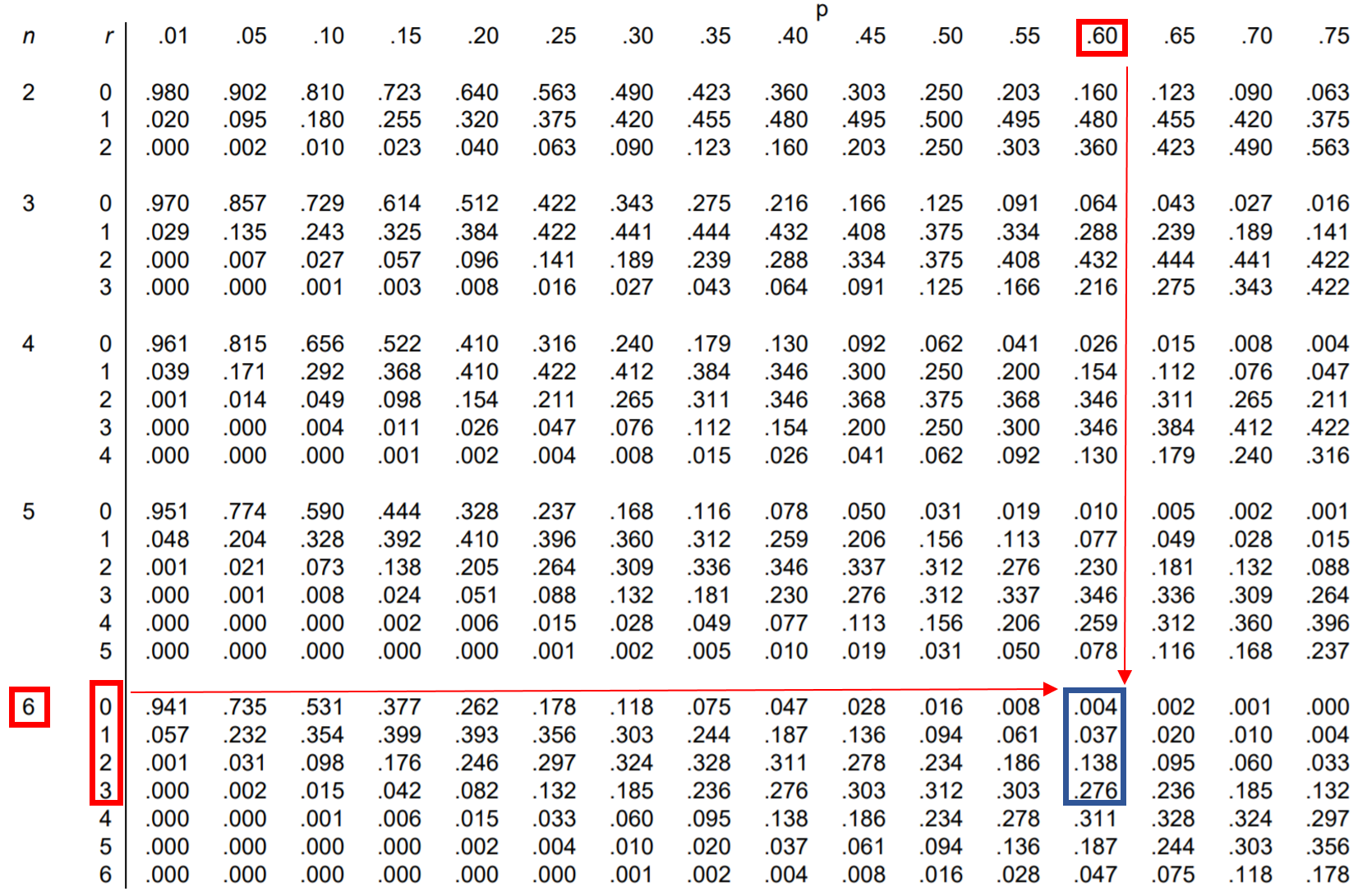
จากตาราง P(น้อยกว่า 4) = .004 + .037 + .138 + .276 = 0.455

ความน่าจะเป็นที่เจสสิก้าโยนโทษน้อยกว่า 4 ครั้งคือ 0.455

ตัวอย่างที่ 3

คำถาม: เจสสิก้าทำ 60% ของความพยายามในการโยนโทษของเธอ ถ้าเธอโยนโทษ 6 ครั้ง ความน่าจะเป็นที่เธอโยนโทษ 4 ครั้งขึ้นไปเป็นเท่าใด

ในการค้นหาความน่าจะเป็นนี้ เราต้องเพิ่มความน่าจะเป็นต่อไปนี้:

P(ได้ 4 หรือมากกว่า) = P(ได้ 4) + P(ได้ 5) + P(ได้ 6)

ดังนั้นเราจึงสามารถค้นหาความน่าจะเป็นทั้งสามอย่างนี้ในตารางการแจกแจงแบบทวินามแล้วบวกเข้าด้วยกัน:

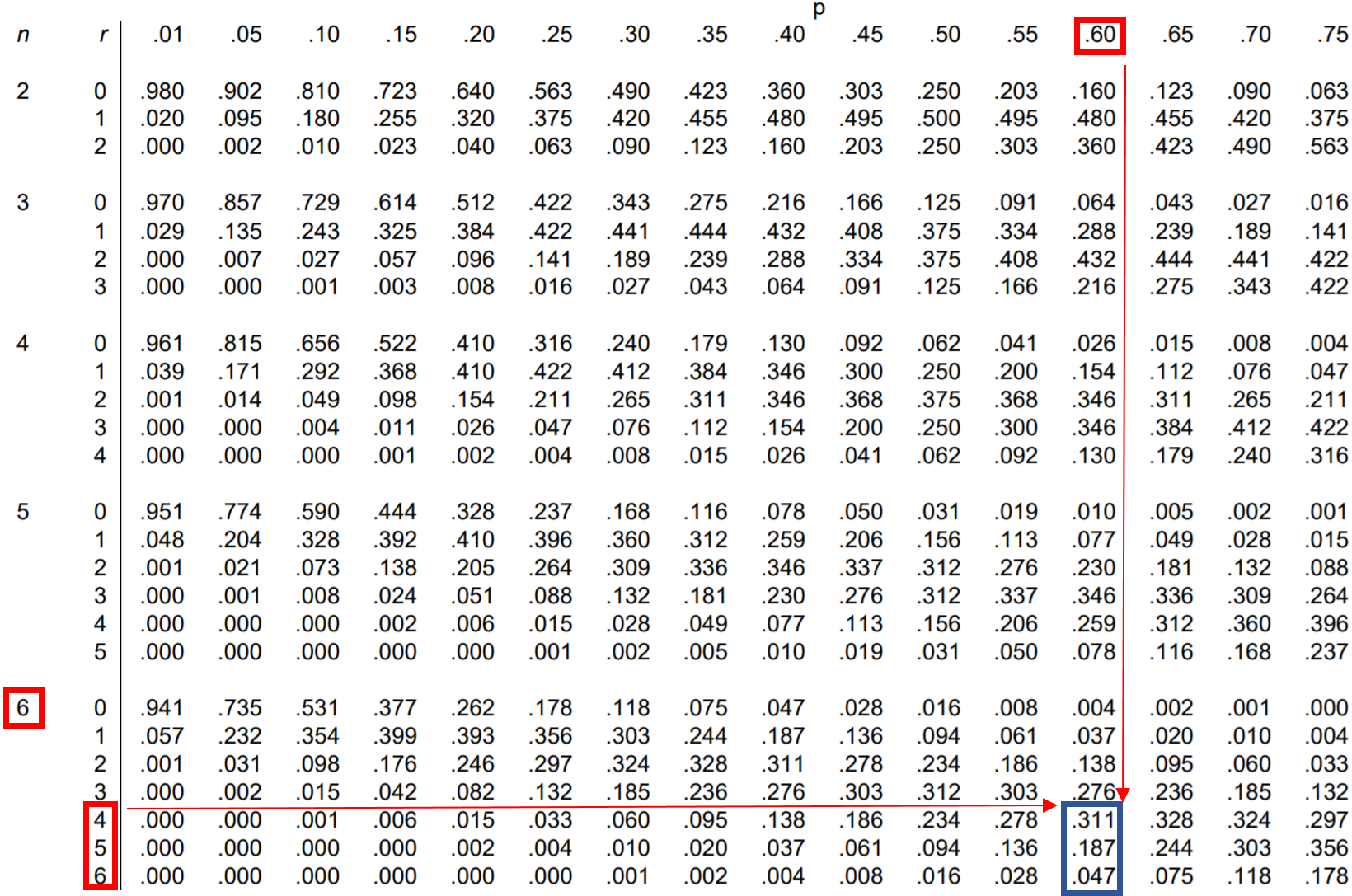
จากตาราง P(ได้ 4 หรือมากกว่า) = .311 + .187 + .047 = 0.545

ความน่าจะเป็นที่เจสสิก้าโยนโทษ 4 ครั้งขึ้นไปคือ 0.545