วิธีอ่านเมทริกซ์สหสัมพันธ์

ในทางสถิติ เรามักจะพยายามทำความเข้าใจความสัมพันธ์ระหว่างตัวแปรสองตัว

ตัวอย่างเช่น เราอาจต้องการทำความเข้าใจความสัมพันธ์ระหว่างจำนวนชั่วโมงที่นักเรียนเรียนกับเกรดที่พวกเขาได้รับจากการสอบ

วิธีหนึ่งในการหาปริมาณความสัมพันธ์นี้คือการใช้ สัมประสิทธิ์ สหสัมพันธ์แบบเพียร์สัน ซึ่งเป็นหน่วยวัดความสัมพันธ์เชิงเส้นระหว่างตัวแปรสองตัว มีค่าระหว่าง -1 ถึง 1 โดยที่:

• -1 บ่งชี้ถึงความสัมพันธ์เชิงเส้นเชิงลบอย่างสมบูรณ์ระหว่างตัวแปรสองตัว
• 0 บ่งชี้ว่าไม่มีความสัมพันธ์เชิงเส้นระหว่างตัวแปรสองตัว
• 1 บ่งชี้ความสัมพันธ์เชิงเส้นเชิงบวกอย่างสมบูรณ์ระหว่างตัวแปรสองตัว

ยิ่งค่าสัมประสิทธิ์สหสัมพันธ์จากศูนย์มากเท่าใด ความสัมพันธ์ระหว่างตัวแปรทั้งสองก็จะยิ่งแข็งแกร่งขึ้นเท่านั้น

ที่เกี่ยวข้อง: อะไรคือความสัมพันธ์ที่ “แข็งแกร่ง”?

แต่ในบางกรณี เราต้องการเข้าใจความสัมพันธ์ระหว่างตัวแปรหลายคู่ ในกรณีเหล่านี้ เราสามารถสร้าง เมทริกซ์สหสัมพันธ์ ซึ่งเป็นตารางสี่เหลี่ยมที่แสดงค่าสัมประสิทธิ์สหสัมพันธ์ระหว่างตัวแปรหลายตัว

ตัวอย่างเมทริกซ์สหสัมพันธ์

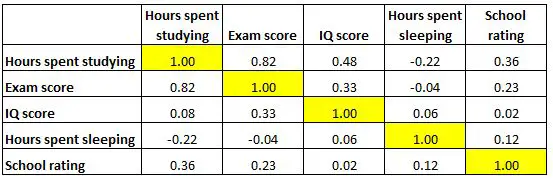
เมทริกซ์สหสัมพันธ์ด้านล่างแสดงค่าสัมประสิทธิ์สหสัมพันธ์ระหว่างตัวแปรที่เกี่ยวข้องกับการศึกษาหลายตัว:

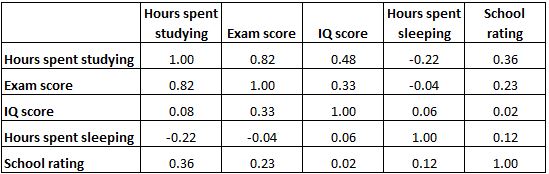
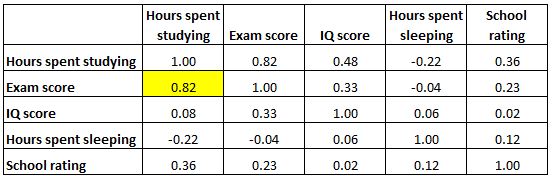
แต่ละเซลล์ในตารางแสดงความสัมพันธ์ระหว่างตัวแปรเฉพาะสองตัว ตัวอย่างเช่น เซลล์ที่ไฮไลต์ด้านล่างแสดงว่าความสัมพันธ์ระหว่าง “ชั่วโมงการเรียน” และ “เกรดสอบ” คือ 0.82 ซึ่งบ่งชี้ว่ามีความสัมพันธ์เชิงบวกอย่างยิ่ง ชั่วโมงเรียนที่มากขึ้นมีความเชื่อมโยงอย่างใกล้ชิดกับคะแนนสอบที่สูงขึ้น

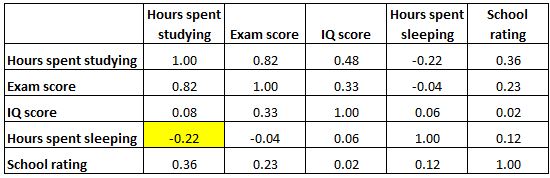
และเซลล์ที่ไฮไลต์ด้านล่างแสดงให้เห็นว่าความสัมพันธ์ระหว่าง “ชั่วโมงที่ใช้ในการเรียน” และ “ชั่วโมงที่ใช้ไปกับการนอนหลับ” คือ -0.22 ซึ่งบ่งชี้ว่ามีความสัมพันธ์เชิงลบเพียงเล็กน้อย ชั่วโมงเรียนที่มากขึ้นสัมพันธ์กับการใช้เวลานอนน้อยลง

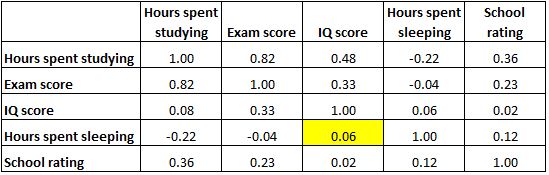
และเซลล์ที่ไฮไลต์ด้านล่างแสดงให้เห็นว่าความสัมพันธ์ระหว่าง “ชั่วโมงที่ใช้ในการนอนหลับ” และ “คะแนน IQ” คือ 0.06 ซึ่งบ่งชี้ว่าโดยพื้นฐานแล้วพวกมันไม่มีความสัมพันธ์กัน มีความเกี่ยวข้องน้อยมากระหว่างจำนวนชั่วโมงที่นักเรียนนอนหลับและคะแนนไอคิวของพวกเขา

โปรดทราบว่าค่าสัมประสิทธิ์สหสัมพันธ์ตามแนวทแยงของตารางมีค่าเท่ากับ 1 เนื่องจากตัวแปรแต่ละตัวมีความสัมพันธ์อย่างสมบูรณ์กับตัวมันเอง เซลล์เหล่านี้ไม่มีประโยชน์สำหรับการตีความ

การแปรผันของเมทริกซ์สหสัมพันธ์

โปรดทราบว่าเมทริกซ์สหสัมพันธ์มีความสมมาตรอย่างสมบูรณ์แบบ ตัวอย่างเช่น เซลล์ด้านบนขวาจะแสดงค่าเดียวกันกับเซลล์ด้านล่างซ้ายทุกประการ:

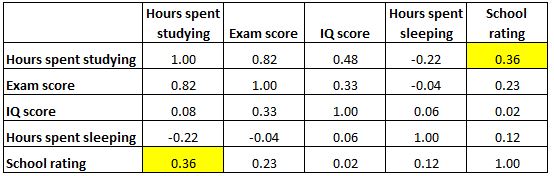
แท้จริงแล้ว ทั้งสองเซลล์วัดความสัมพันธ์ระหว่าง “ชั่วโมงที่ใช้เรียน” และ “เกรดของโรงเรียน”

เนื่องจากเมทริกซ์สหสัมพันธ์มีความสมมาตร ครึ่งหนึ่งของค่าสัมประสิทธิ์สหสัมพันธ์ที่แสดงในเมทริกซ์จึงซ้ำซ้อนและไม่จำเป็น ดังนั้น บางครั้งจะแสดงเพียงครึ่งหนึ่งของเมทริกซ์สหสัมพันธ์เท่านั้น:

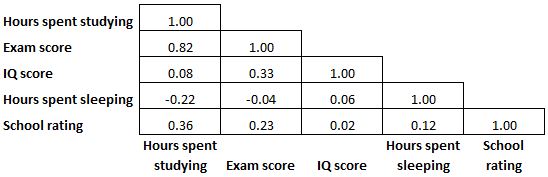
และบางครั้งเมทริกซ์สหสัมพันธ์จะมีสีเหมือนแผนที่ความร้อนเพื่อทำให้ค่าสัมประสิทธิ์สหสัมพันธ์อ่านง่ายยิ่งขึ้น:

เมื่อใดควรใช้เมทริกซ์สหสัมพันธ์

ในทางปฏิบัติ เมทริกซ์สหสัมพันธ์มักใช้ด้วยเหตุผลสามประการ:

1. เมทริกซ์สหสัมพันธ์สรุปชุดข้อมูลได้อย่างสะดวก

เมทริกซ์สหสัมพันธ์เป็นวิธีง่ายๆ ในการสรุปความสัมพันธ์ระหว่างตัวแปรทั้งหมดในชุดข้อมูล ตัวอย่างเช่น สมมติว่าเรามีชุดข้อมูลต่อไปนี้ซึ่งมีข้อมูลต่อไปนี้สำหรับนักเรียน 1,000 คน:

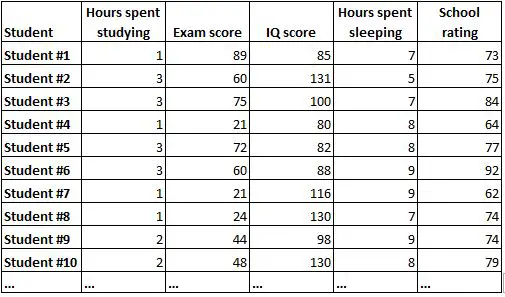
มันจะยากมากที่จะเข้าใจความสัมพันธ์ระหว่างตัวแปรแต่ละตัวเพียงแค่ดูข้อมูลดิบ โชคดีที่เมทริกซ์สหสัมพันธ์สามารถช่วยให้เราเข้าใจความสัมพันธ์ระหว่างตัวแปรแต่ละคู่ได้อย่างรวดเร็ว

2. เมทริกซ์สหสัมพันธ์ทำหน้าที่เป็นการวินิจฉัยการถดถอย

สมมติฐานหลักข้อหนึ่งของ การถดถอยเชิงเส้นพหุคูณ คือไม่มีตัวแปรอิสระในแบบจำลองที่มีความสัมพันธ์อย่างมากกับตัวแปรอื่นๆ ในแบบจำลอง

เมื่อตัวแปรอิสระสองตัวมีความสัมพันธ์กันสูง จะส่งผลให้เกิดปัญหาที่เรียกว่า multicollinearity และอาจทำให้ตีความผลลัพธ์ของการถดถอยได้ยาก

วิธีที่ง่ายที่สุดวิธีหนึ่งในการระบุปัญหาหลายคอลลิเนียริตี้ที่อาจเกิดขึ้นคือการดูเมทริกซ์สหสัมพันธ์และตรวจดูด้วยสายตาว่ามีตัวแปรตัวใดมีความสัมพันธ์กันสูงหรือไม่

3. เมทริกซ์สหสัมพันธ์สามารถใช้เป็นข้อมูลเข้าในการวิเคราะห์อื่นๆ ได้

เมทริกซ์สหสัมพันธ์ถูกใช้เป็นข้อมูลป้อนเข้าสำหรับการวิเคราะห์ที่ซับซ้อนอื่นๆ เช่น การวิเคราะห์ปัจจัยเชิงสำรวจ และแบบจำลองสมการโครงสร้าง

แหล่งข้อมูลเพิ่มเติม

บทช่วยสอนต่อไปนี้จะอธิบายวิธีสร้างเมทริกซ์สหสัมพันธ์โดยใช้ซอฟต์แวร์ทางสถิติต่างๆ

วิธีสร้างเมทริกซ์สหสัมพันธ์ใน Excel
วิธีสร้างเมทริกซ์สหสัมพันธ์ใน SPSS
วิธีสร้างเมทริกซ์สหสัมพันธ์ใน Stata
วิธีสร้างเมทริกซ์สหสัมพันธ์ใน Python