วิธีใช้ข้อผิดพลาดมาตรฐานที่แข็งแกร่งในการถดถอยใน stata

การถดถอยเชิงเส้นพหุคูณ เป็นวิธีการที่เราสามารถใช้เพื่อทำความเข้าใจความสัมพันธ์ระหว่างตัวแปรอธิบายหลายตัวและตัวแปรตอบสนอง

น่าเสียดายที่ปัญหาที่มักเกิดขึ้นในการถดถอยเรียกว่า เฮเทอโรสซิดาสติกซิตี ซึ่งมีการเปลี่ยนแปลงอย่างเป็นระบบในด้านความแปรปรวนของค่าคงเหลือในช่วงของค่าที่วัดได้

สิ่งนี้นำไปสู่การเพิ่มขึ้นของความแปรปรวนของการประมาณค่าสัมประสิทธิ์การถดถอย แต่แบบจำลองการถดถอยไม่ได้คำนึงถึงสิ่งนี้ ซึ่งทำให้มีโอกาสมากขึ้นที่แบบจำลองการถดถอยจะอ้างว่าคำในแบบจำลองนั้นมีนัยสำคัญทางสถิติ ทั้งที่ในความเป็นจริงกลับไม่มีนัยสำคัญ

วิธีหนึ่งในการอธิบายปัญหานี้คือการใช้ ข้อผิดพลาดมาตรฐานที่เข้มงวด ซึ่งจะ “แข็งแกร่ง” มากกว่าสำหรับปัญหาแบบเฮเทอโรสเกดาสติก และมีแนวโน้มที่จะให้การวัดข้อผิดพลาดมาตรฐานที่แท้จริงของค่าสัมประสิทธิ์การถดถอยได้แม่นยำยิ่งขึ้น

บทช่วยสอนนี้จะอธิบายวิธีใช้ข้อผิดพลาดมาตรฐานที่แข็งแกร่งในการวิเคราะห์การถดถอยใน Stata

ตัวอย่าง: ข้อผิดพลาดมาตรฐานที่แข็งแกร่งใน Stata

เราจะใช้ชุดข้อมูล Stata ที่ผสานรวม โดยอัตโนมัติ เพื่อแสดงวิธีใช้ข้อผิดพลาดมาตรฐานที่เข้มงวดในการถดถอย

ขั้นตอนที่ 1: โหลดและแสดงข้อมูล

ขั้นแรก ให้ใช้คำสั่งต่อไปนี้เพื่อโหลดข้อมูล:

การใช้งานระบบอัตโนมัติ

จากนั้นแสดงข้อมูลดิบโดยใช้คำสั่งต่อไปนี้:

พี่ชาย

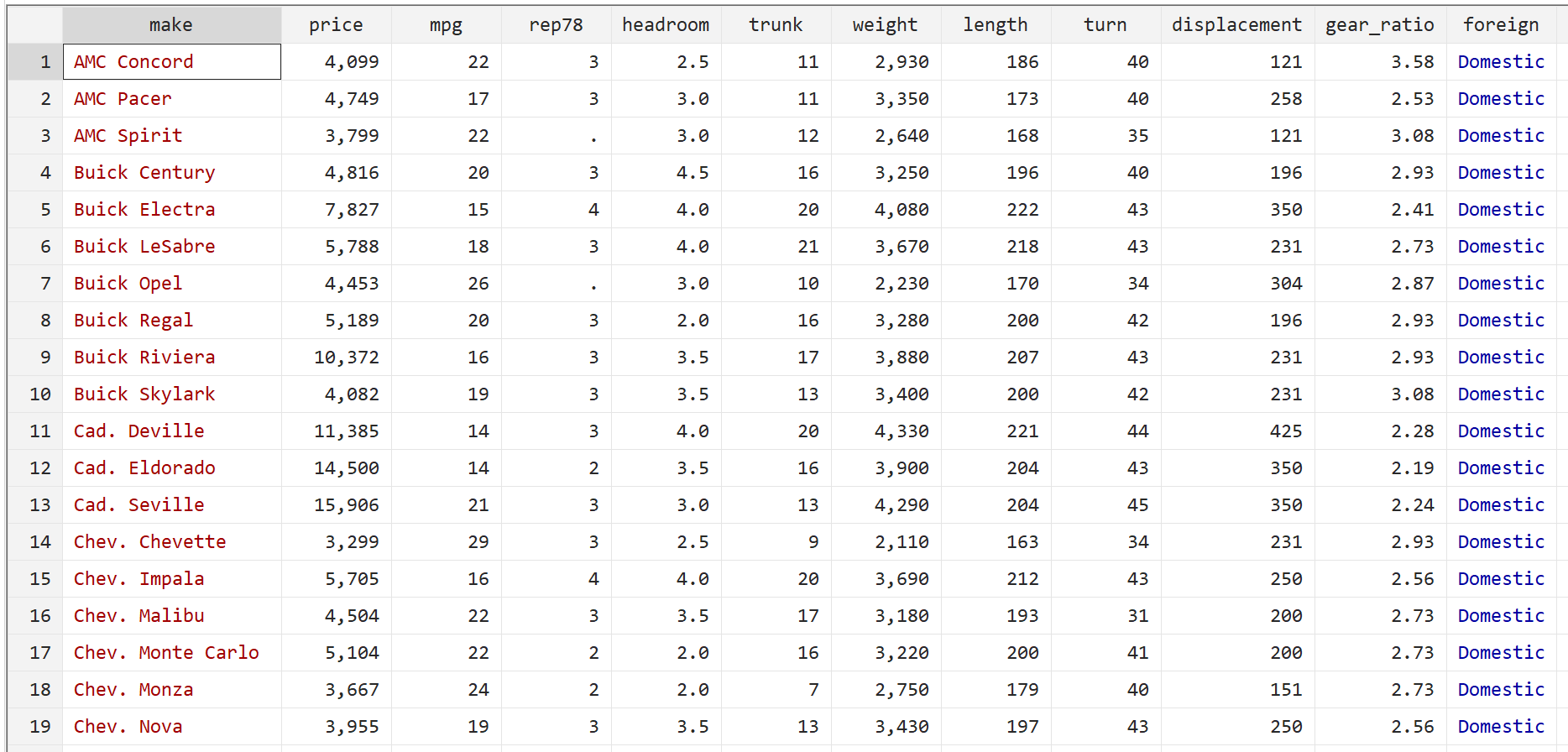
ขั้นตอนที่ 2: ดำเนินการถดถอยเชิงเส้นหลายรายการโดยไม่มีข้อผิดพลาดมาตรฐานที่แข็งแกร่ง

ต่อไป เราจะป้อนคำสั่งต่อไปนี้เพื่อทำการถดถอยเชิงเส้นพหุคูณโดยใช้ ราคา เป็นตัวแปรตอบสนอง และใช้ mpg และ น้ำหนัก เป็นตัวแปรอธิบาย:

ราคาถดถอย mpg น้ำหนัก

ขั้นตอนที่ 3: ดำเนินการถดถอยเชิงเส้นหลายรายการโดยใช้ข้อผิดพลาดมาตรฐานที่แข็งแกร่ง

ตอนนี้เราจะทำการถดถอยเชิงเส้นพหุคูณแบบเดียวกันทุกประการ แต่คราวนี้เราจะใช้คำสั่ง vce(robust) เพื่อให้ Stata รู้วิธีใช้ข้อผิดพลาดมาตรฐานที่แข็งแกร่ง:

ราคาถดถอย mpg น้ำหนัก, vce (แข็งแกร่ง)

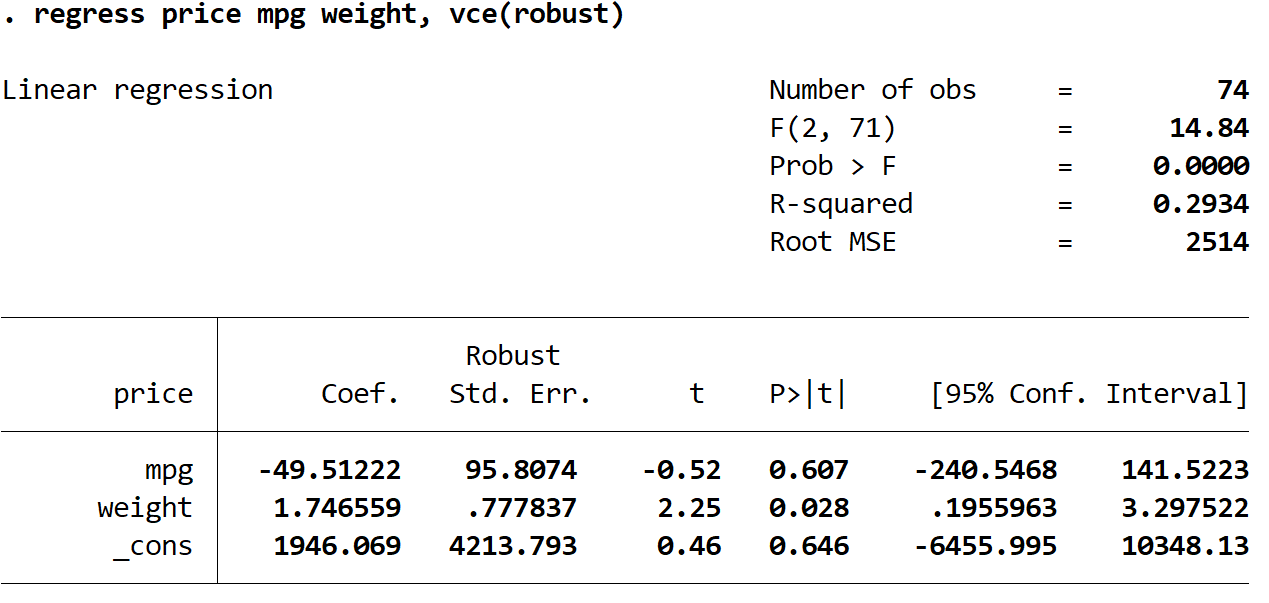
มีสิ่งที่น่าสนใจบางประการที่ควรทราบที่นี่:

1. การประมาณค่าสัมประสิทธิ์ยังคงเหมือนเดิม เมื่อเราใช้ข้อผิดพลาดมาตรฐานที่เข้มงวด การประมาณค่าสัมประสิทธิ์จะไม่เปลี่ยนแปลงเลย โปรดทราบว่าการประมาณค่าสัมประสิทธิ์สำหรับ MPG น้ำหนัก และค่าคงที่จะเป็นดังนี้สำหรับการถดถอยทั้งสอง:

• mpg: -49.51222
• น้ำหนัก: 1.746559
• _ต่อ: 1946.069

2. ข้อผิดพลาดมาตรฐานมีการเปลี่ยนแปลง โปรดทราบว่าเมื่อเราใช้ข้อผิดพลาดมาตรฐานที่เข้มงวด ข้อผิดพลาดมาตรฐานสำหรับการประมาณค่าสัมประสิทธิ์แต่ละรายการจะเพิ่มขึ้น

หมายเหตุ: ในกรณีส่วนใหญ่ ข้อผิดพลาดมาตรฐานที่เข้มงวดจะมีขนาดใหญ่กว่าข้อผิดพลาดมาตรฐานปกติ แต่ในบางกรณีที่เกิดขึ้นไม่บ่อยนัก อาจเป็นไปได้ว่าข้อผิดพลาดมาตรฐานที่เข้มงวดจะมีขนาดเล็กลง

3. สถิติการทดสอบของแต่ละสัมประสิทธิ์มีการเปลี่ยนแปลง โปรดทราบว่าค่าสัมบูรณ์ของสถิติการทดสอบแต่ละรายการ t ลดลง ผลก็คือ สถิติการทดสอบจะคำนวณเป็นค่าสัมประสิทธิ์โดยประมาณหารด้วยข้อผิดพลาดมาตรฐาน ดังนั้น ยิ่งค่าความผิดพลาดมาตรฐานมาก ค่าสัมบูรณ์ของสถิติการทดสอบก็จะยิ่งน้อยลง

4. ค่า p มีการเปลี่ยนแปลง โปรดทราบว่าค่า p สำหรับแต่ละตัวแปรก็เพิ่มขึ้นเช่นกัน เนื่องจากสถิติการทดสอบที่น้อยกว่าจะสัมพันธ์กับค่า p ที่มากกว่า

แม้ว่าค่า p จะเปลี่ยนไปสำหรับสัมประสิทธิ์ของเรา แต่ตัวแปร mpg ก็ยังไม่มีนัยสำคัญทางสถิติที่ α = 0.05 และ น้ำหนัก ตัวแปรยังคงมีนัยสำคัญทางสถิติที่ α = 0.05