สถิติเชิงพรรณนาหรือเชิงอนุมาน: อะไรคือความแตกต่าง?

มีสองสาขาหลักในสาขาสถิติ:

• สถิติเชิงพรรณนา
• สถิติอนุมาน

บทช่วยสอนนี้จะอธิบายความแตกต่างระหว่างสองสาขาและเหตุใดแต่ละสาขาจึงมีประโยชน์ในบางสถานการณ์

สถิติ เชิง พรรณนา

โดย สรุป สถิติเชิง พรรณนามีจุดมุ่งหมายเพื่อ อธิบาย ชุด ข้อมูลดิบ โดยใช้สถิติสรุป กราฟ และตาราง

สถิติเชิงพรรณนามีประโยชน์เนื่องจากช่วยให้คุณเข้าใจกลุ่มข้อมูลได้เร็วและง่ายกว่าการดูแถวและแถวของค่าข้อมูลดิบ

ตัวอย่างเช่น สมมติว่าเรามีชุดข้อมูลดิบที่แสดงคะแนนสอบของนักเรียน 1,000 คนในโรงเรียนแห่งหนึ่ง เราอาจสนใจคะแนนสอบเฉลี่ยตลอดจนการกระจายคะแนนสอบ

เมื่อใช้สถิติเชิงพรรณนา เราสามารถหาคะแนนเฉลี่ยและสร้างกราฟที่ช่วยให้เห็นภาพการกระจายตัวของคะแนนได้

สิ่งนี้ช่วยให้เราเข้าใจคะแนนสอบของนักเรียนได้ง่ายกว่าการดูข้อมูลดิบมาก

สถิติเชิงพรรณนารูปแบบทั่วไป

สถิติเชิงพรรณนาทั่วไปมีสามรูปแบบ:

1. สถิติสรุป เป็นสถิติที่ สรุป ข้อมูลโดยใช้ตัวเลขเพียงตัวเดียว สถิติสรุปทั่วไปมี 2 ประเภท:

• การวัดแนวโน้มจากศูนย์กลาง : ตัวเลขเหล่านี้อธิบายว่าศูนย์กลางของชุดข้อมูลอยู่ที่ใด ตัวอย่างได้แก่ ค่าเฉลี่ย   และ ค่ามัธยฐาน
• มาตรการการกระจาย: ตัวเลขเหล่านี้อธิบายการกระจายของค่าในชุดข้อมูล ตัวอย่าง ได้แก่ ช่วง ช่วงระหว่างควอไทล์ ค่าเบี่ยงเบนมาตรฐาน และ ความแปรปรวน

2. กราฟิก . แผนภูมิช่วยให้เราเห็นภาพข้อมูล แผนภูมิประเภททั่วไปที่ใช้ในการแสดงภาพข้อมูล ได้แก่ แผนภูมิกล่อง ฮิสโตแกรม แผนภูมิก้านและใบ และ แผนภูมิกระจาย

3. ตาราง . ตารางสามารถช่วยให้เราเข้าใจวิธีการกระจายข้อมูล ตารางประเภททั่วไปคือ ตารางความถี่ ซึ่งบอกเราว่าค่าข้อมูลจำนวนเท่าใดอยู่ในช่วงที่กำหนด

ตัวอย่างการใช้สถิติเชิงพรรณนา

ตัวอย่างต่อไปนี้แสดงให้เห็นว่าเราอาจใช้สถิติเชิงพรรณนาในโลกแห่งความเป็นจริงได้อย่างไร

สมมติว่านักเรียน 1,000 คนในโรงเรียนบางแห่งทำแบบทดสอบเดียวกันทั้งหมด เราต้องการทำความเข้าใจการกระจายตัวของผลการทดสอบ ดังนั้นเราจึงใช้สถิติเชิงพรรณนาต่อไปนี้:

1. สถิติสรุป

เฉลี่ย: 82.13 . สิ่งนี้บอกเราว่าคะแนนสอบเฉลี่ยของนักเรียน 1,000 คนคือ 82.13

ค่ามัธยฐาน: 84 นี่บอกเราว่าครึ่งหนึ่งของนักเรียนทั้งหมดทำคะแนนได้มากกว่า 84 และอีกครึ่งหนึ่งได้คะแนนต่ำกว่า 84

สูงสุด: 100 ต่ำสุด: 45 สิ่งนี้บอกเราว่าคะแนนสูงสุดที่นักเรียนคนใดก็ตามได้รับคือ 100 และคะแนนขั้นต่ำคือ 45 ช่วง ซึ่งบอกเราถึงความแตกต่างระหว่างคะแนนสูงสุดและต่ำสุดคือ 55

2. กราฟิก

เพื่อให้เห็นภาพการกระจายตัวของผลการทดสอบ เราสามารถสร้างฮิสโตแกรม ซึ่งเป็นแผนภูมิประเภทหนึ่งที่ใช้แท่งสี่เหลี่ยมเพื่อแสดงความถี่

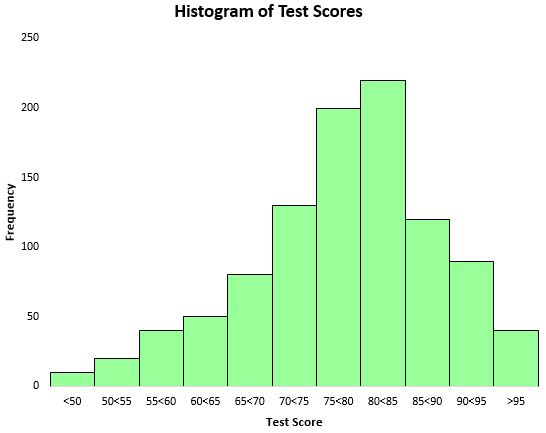
จากฮิสโตแกรมนี้ เราจะเห็นว่าการกระจายตัวของคะแนนการทดสอบเป็นรูประฆังโดยประมาณ นักเรียนส่วนใหญ่ทำคะแนนได้ระหว่าง 70 ถึง 90 ในขณะที่มีเพียงไม่กี่คนที่ได้คะแนนสูงกว่า 95 และคะแนนน้อยกว่า 50 อีกด้วย

3. ตาราง

อีกวิธีง่ายๆ ในการทำความเข้าใจการกระจายคะแนนคือการสร้างตารางความถี่ ตัวอย่างเช่น ตารางความถี่ต่อไปนี้แสดงเปอร์เซ็นต์ของนักเรียนที่ทำคะแนนระหว่างช่วงต่างๆ:

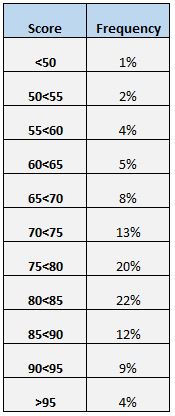
เราจะเห็นว่ามีเพียง 4% ของนักเรียนทั้งหมดที่ทำคะแนนได้มากกว่า 95 นอกจากนี้เรายังเห็นว่า (12% + 9% + 4% = ) 25% ของนักเรียนทั้งหมดทำคะแนนได้ 85 ขึ้นไป

ตารางความถี่มีประโยชน์อย่างยิ่งหากเราต้องการทราบว่าค่าข้อมูลเป็นเปอร์เซ็นต์สูงหรือต่ำกว่าค่าที่กำหนด ตัวอย่างเช่น สมมติว่าโรงเรียนถือว่าคะแนนสอบที่ “ยอมรับได้” เป็นคะแนนใดๆ ที่สูงกว่า 75

เมื่อดูตารางความถี่ เราจะเห็นได้ง่ายว่า (20% + 22% + 12% + 9% + 4% = ) 67% ของนักเรียนได้รับคะแนนที่ยอมรับได้ในการทดสอบ

สถิติอนุมาน

โดยสรุป สถิติเชิงอนุมาน ใช้ตัวอย่างข้อมูลขนาดเล็กเพื่อสรุป ผล เกี่ยวกับประชากรกลุ่มใหญ่ที่ใช้สุ่มตัวอย่าง

ตัวอย่างเช่น เราอาจต้องการทำความเข้าใจความชอบทางการเมืองของผู้คนหลายล้านคนในประเทศหนึ่งๆ

อย่างไรก็ตาม การสำรวจทุกคนในประเทศอาจใช้เวลานานและมีราคาแพงเกินไป ดังนั้น เราจะทำการสำรวจชาวอเมริกันจำนวน 1,000 คนที่มีขนาดเล็กกว่าแทน และใช้ผลการสำรวจเพื่อสรุปเกี่ยวกับประชากรโดยรวม

นี่คือหลักฐานทั้งหมดของสถิติเชิงอนุมาน: เราต้องการตอบคำถามเกี่ยวกับประชากร ดังนั้นเราจึงได้รับข้อมูลสำหรับกลุ่มตัวอย่างเล็กๆ ของประชากรนั้น และใช้ข้อมูลตัวอย่างในการอนุมานเกี่ยวกับประชากร

ความสำคัญของตัวอย่างที่เป็นตัวแทน

เพื่อให้มั่นใจในความสามารถของเราในการใช้ตัวอย่างเพื่อสรุปเกี่ยวกับประชากร เราต้องแน่ใจว่าเรามี ตัวอย่างที่เป็นตัวแทน กล่าวคือ ตัวอย่างที่มีลักษณะเฉพาะของบุคคลในประชากร กลุ่มตัวอย่างตรงกับกลุ่มตัวอย่างอย่างใกล้ชิด ลักษณะเฉพาะ. ของประชากรโดยรวม

ตามหลักการแล้ว เราต้องการให้ตัวอย่างของเรามีลักษณะคล้ายกับ “เวอร์ชันจิ๋ว” ของประชากรของเรา ดังนั้น หากเราต้องการสรุปเกี่ยวกับประชากรของนักเรียนที่ประกอบด้วยเด็กผู้หญิง 50% และเด็กผู้ชาย 50% ตัวอย่างของเราจะไม่เป็นตัวแทนได้หากรวมเด็กผู้ชาย 90% และเด็กผู้หญิงเพียง 10% เท่านั้น

หากกลุ่มตัวอย่างของเราไม่เหมือนกับประชากรโดยรวม เราไม่สามารถสรุปผลลัพธ์จากกลุ่มตัวอย่างกับประชากรโดยรวมได้อย่างมั่นใจ

วิธีการรับตัวอย่างตัวแทน

เพื่อเพิ่มโอกาสในการได้รับตัวอย่างที่เป็นตัวแทน คุณควรมุ่งเน้นไปที่สองสิ่ง:

1. ตรวจสอบให้แน่ใจว่าคุณใช้วิธีการสุ่มตัวอย่าง

มี วิธีสุ่มตัวอย่าง หลายวิธีที่คุณสามารถใช้ได้ซึ่งมีแนวโน้มที่จะสร้างตัวอย่างที่เป็นตัวแทน ซึ่งรวมถึง:

• สุ่มตัวอย่างง่ายๆ
• การสุ่มตัวอย่างอย่างเป็นระบบ
• ตัวอย่างแบบสุ่มแบบคลัสเตอร์
• ตัวอย่างแบบแบ่งชั้น

วิธีการสุ่มตัวอย่างมีแนวโน้มที่จะสร้างตัวอย่างที่เป็นตัวแทน เนื่องจากสมาชิกแต่ละคนมีโอกาสเท่ากันที่จะถูกรวมไว้ในกลุ่มตัวอย่าง

2. ตรวจสอบให้แน่ใจว่าขนาดตัวอย่างของคุณใหญ่เพียงพอ

นอกเหนือจากการใช้วิธีการสุ่มตัวอย่างที่เหมาะสมแล้ว สิ่งสำคัญคือต้องแน่ใจว่าตัวอย่างมีขนาดใหญ่เพียงพอเพื่อให้คุณมีข้อมูลเพียงพอที่จะสรุปกับประชากรกลุ่มใหญ่ได้

ในการกำหนดขนาดตัวอย่างของคุณ คุณต้องพิจารณาขนาดของประชากรที่คุณกำลังศึกษา ระดับความเชื่อมั่นที่คุณต้องการใช้ และขอบเขตของข้อผิดพลาดที่คุณถือว่ายอมรับได้

โชคดีที่คุณสามารถใช้เครื่องคิดเลขออนไลน์เพื่อป้อนค่าเหล่านี้และดูว่าขนาดตัวอย่างของคุณควรเป็นเท่าใด

รูปแบบทั่วไปของสถิติเชิงอนุมาน

สถิติเชิงอนุมานทั่วไปมีสามรูปแบบ:

1. การทดสอบสมมติฐาน

เรามักต้องการตอบคำถามเกี่ยวกับประชากร เช่น:

• เปอร์เซ็นต์ของคนในโอไฮโอที่สนับสนุนผู้สมัคร A มากกว่า 50% หรือไม่?
• ความสูงเฉลี่ยของต้นไม้บางชนิดเท่ากับ 14 นิ้วหรือไม่?
• ความสูงเฉลี่ยของนักเรียนที่โรงเรียน A และโรงเรียน B แตกต่างกันหรือไม่?

เพื่อตอบคำถามเหล่านี้ เราสามารถทำได้ การทดสอบสมมติฐาน ซึ่งช่วยให้เราใช้ข้อมูลจากกลุ่มตัวอย่างเพื่อสรุปเกี่ยวกับประชากรได้

2. ช่วงความมั่นใจ

บางครั้งเราต้องการประมาณค่าที่แน่นอนของประชากร ตัวอย่างเช่น เราอาจสนใจความสูงเฉลี่ยของพืชบางชนิดในออสเตรเลีย

แทนที่จะไปตรวจวัดพืชทุกต้นในประเทศ เราสามารถเก็บตัวอย่างพืชเล็กๆ และวัดแต่ละต้นได้ จากนั้นเราสามารถใช้ความสูงเฉลี่ยของต้นไม้ในกลุ่มตัวอย่างเพื่อประมาณความสูงเฉลี่ยของประชากรได้

อย่างไรก็ตาม ตัวอย่างของเราไม่สามารถให้การประมาณประชากรที่สมบูรณ์แบบได้ โชคดีที่เราสามารถอธิบายความไม่แน่นอนนี้ได้โดยการสร้าง ช่วงความเชื่อมั่น ซึ่งให้ช่วงของค่าภายในที่เรามั่นใจว่าพารามิเตอร์ประชากรที่แท้จริงอยู่

ตัวอย่างเช่น เราสามารถสร้างช่วงความเชื่อมั่น 95% ที่ [13.2, 14.8] ซึ่งหมายความว่าเรามั่นใจ 95% ว่าความสูงเฉลี่ยที่แท้จริงของพืชชนิดนี้อยู่ระหว่าง 13.2 นิ้วถึง 14.8 นิ้ว

3. การถดถอย .

บางครั้งเราต้องการเข้าใจความสัมพันธ์ระหว่างตัวแปรสองตัวในกลุ่มประชากร

ตัวอย่างเช่น สมมติว่าเราต้องการทราบว่า ชั่วโมงเรียนต่อสัปดาห์ เกี่ยวข้องกับ คะแนนสอบหรือ ไม่ เพื่อตอบคำถามนี้ เราสามารถใช้เทคนิคที่เรียกว่า การวิเคราะห์การถดถอย

ดังนั้นเราจึงสามารถดูจำนวนชั่วโมงเรียนและคะแนนการทดสอบของนักเรียน 100 คน และทำการวิเคราะห์การถดถอยเพื่อดูว่ามีความสัมพันธ์ที่มีนัยสำคัญระหว่างตัวแปรทั้งสองหรือไม่

หาก พบว่าค่า p ของการถดถอยมีนัยสำคัญ เราสามารถสรุปได้ว่ามีความสัมพันธ์ที่มีนัยสำคัญระหว่างตัวแปรทั้งสองนี้ในประชากรนักเรียนโดยรวม

ความแตกต่างระหว่างสถิติเชิงพรรณนาและสถิติเชิงอนุมาน

โดยสรุป ความแตกต่างระหว่างสถิติเชิงพรรณนาและสถิติเชิงอนุมานสามารถอธิบายได้ดังนี้

สถิติเชิงพรรณนา ใช้สถิติสรุป กราฟ และตารางเพื่อ อธิบาย ชุดข้อมูล

สิ่งนี้มีประโยชน์ในการช่วยให้เราเข้าใจชุดข้อมูลได้อย่างรวดเร็วและง่ายดาย โดยไม่ต้องผ่านค่าข้อมูลแต่ละรายการทั้งหมด

สถิติเชิงอนุมาน ใช้ตัวอย่างเพื่อสรุป ผล เกี่ยวกับประชากรกลุ่มใหญ่

คุณอาจตัดสินใจใช้วิธีการใดวิธีหนึ่งต่อไปนี้ ขึ้นอยู่กับคำถามที่คุณต้องการตอบเกี่ยวกับประชากร: การทดสอบสมมติฐาน ช่วงความเชื่อมั่น และการวิเคราะห์การถดถอย

หากคุณเลือกที่จะใช้วิธีใดวิธีหนึ่งเหล่านี้ โปรดทราบว่า ตัวอย่างของคุณจะต้องเป็นตัวแทนของประชากรของคุณ มิฉะนั้นข้อสรุปที่คุณสรุปได้จะไม่น่าเชื่อถือ