สมมติฐานสี่ประการของการถดถอยเชิงเส้น
การถดถอยเชิงเส้น เป็นวิธีการทางสถิติที่มีประโยชน์ที่เราสามารถใช้เพื่อทำความเข้าใจความสัมพันธ์ระหว่างตัวแปรสองตัว นั่นคือ x และ y อย่างไรก็ตาม ก่อนที่จะทำการถดถอยเชิงเส้น เราต้องตรวจสอบให้แน่ใจก่อนว่าเป็นไปตามสมมติฐานสี่ประการ:
1. ความสัมพันธ์เชิงเส้น: มีความสัมพันธ์เชิงเส้นระหว่างตัวแปรอิสระ x และตัวแปรตาม y
2. ความเป็นอิสระ: ส่วนที่เหลือเป็นอิสระ โดยเฉพาะอย่างยิ่งไม่มีความสัมพันธ์ระหว่างข้อมูลตกค้างติดต่อกันในข้อมูลอนุกรมเวลา
3. ความเป็นเนื้อเดียวกัน: สารตกค้างมีความแปรปรวนคงที่ในแต่ละระดับของ x
4. Normality: โมเดลที่เหลือมีการกระจายตามปกติ
หากไม่เป็นไปตามสมมติฐานเหล่านี้ตั้งแต่หนึ่งข้อขึ้นไป ผลลัพธ์ของการถดถอยเชิงเส้นของเราอาจไม่น่าเชื่อถือหรืออาจทำให้เข้าใจผิดได้
ในบทความนี้ เราจะให้คำอธิบายสำหรับแต่ละสมมติฐาน วิธีตรวจสอบว่าเป็นไปตามสมมติฐานหรือไม่ และต้องทำอย่างไรหากไม่เป็นไปตามสมมติฐาน
สมมติฐานที่ 1: ความสัมพันธ์เชิงเส้น
คำอธิบาย
ข้อสันนิษฐานแรกของการถดถอยเชิงเส้นคือมีความสัมพันธ์เชิงเส้นระหว่างตัวแปรอิสระ x และตัวแปรอิสระ y
จะทราบได้อย่างไรว่าเป็นไปตามสมมติฐานนี้
วิธีที่ง่ายที่สุดในการตรวจสอบว่าสมมติฐานนี้เป็นไปตามสมมติฐานหรือไม่คือการสร้างแผนภาพกระจายของ x กับ y วิธีนี้ช่วยให้คุณมองเห็นได้ว่ามีความสัมพันธ์เชิงเส้นตรงระหว่างตัวแปรทั้งสองหรือไม่ หากปรากฏว่าจุดบนโครงเรื่องสามารถวางเป็นเส้นตรงได้ แสดงว่ามีความสัมพันธ์เชิงเส้นบางประเภทระหว่างตัวแปรทั้งสองและเป็นไปตามสมมติฐานนี้
ตัวอย่างเช่น จุดในกราฟด้านล่างดูเหมือนจะตกลงบนเส้นตรง ซึ่งบ่งชี้ว่ามีความสัมพันธ์เชิงเส้นระหว่าง x และ y:

อย่างไรก็ตาม ดูเหมือนจะไม่มีความสัมพันธ์เชิงเส้นระหว่าง x และ y ในกราฟด้านล่าง:
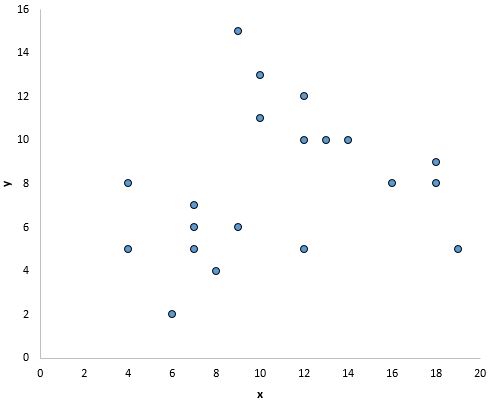
และในกราฟนี้ดูเหมือนว่าจะมีความสัมพันธ์ที่ชัดเจนระหว่าง x และ y แต่ไม่ใช่ความสัมพันธ์เชิงเส้น :
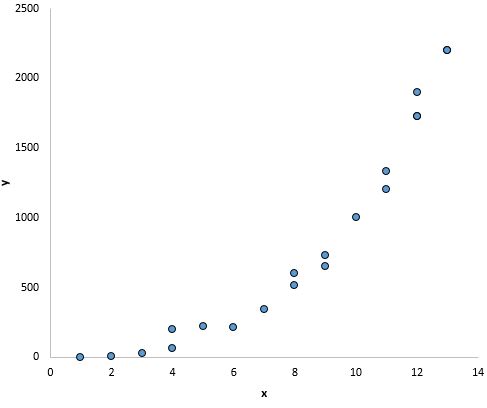
จะทำอย่างไรถ้าสมมติฐานนี้ไม่ได้รับการเคารพ
หากคุณสร้างแผนภาพกระจายของค่าสำหรับ x และ y และพบว่า ไม่มี ความสัมพันธ์เชิงเส้นระหว่างตัวแปรทั้งสอง คุณจะมีหลายตัวเลือก:
1. ใช้การแปลงแบบไม่เชิงเส้นกับตัวแปรอิสระและ/หรือตัวแปรตาม ตัวอย่างทั่วไปได้แก่ การหาบันทึก รากที่สอง หรือส่วนกลับของตัวแปรอิสระและ/หรือตัวแปรตาม
2. เพิ่มตัวแปรอิสระอื่นให้กับโมเดล ตัวอย่างเช่น หากโครงเรื่องของ x เทียบกับ y มีรูปร่างพาราโบลา ก็อาจสมเหตุสมผลที่จะเพิ่ม X 2 เป็นตัวแปรอิสระเพิ่มเติมในแบบจำลอง
สมมติฐานที่ 2: ความเป็นอิสระ
คำอธิบาย
สมมติฐานต่อไปของการถดถอยเชิงเส้นคือส่วนที่เหลือเป็นอิสระจากกัน สิ่งนี้มีความเกี่ยวข้องอย่างยิ่งเมื่อทำงานกับข้อมูลอนุกรมเวลา ตามหลักแล้ว เราไม่ต้องการให้มีแนวโน้มในจำนวนคงเหลือต่อเนื่องกัน ตัวอย่างเช่น สารตกค้างไม่ควรเพิ่มขึ้นอย่างต่อเนื่องเมื่อเวลาผ่านไป
จะทราบได้อย่างไรว่าเป็นไปตามสมมติฐานนี้
วิธีที่ง่ายที่สุดในการทดสอบว่าสมมติฐานนี้ยังคงอยู่หรือไม่คือการดูแผนภาพอนุกรมเวลาของสารตกค้าง ซึ่งเป็นแผนภาพของสารตกค้างเทียบกับเวลา ตามหลักการแล้ว ความสัมพันธ์อัตโนมัติที่ตกค้างส่วนใหญ่ควรอยู่ภายในแถบความเชื่อมั่น 95% รอบศูนย์ ซึ่งอยู่ที่ประมาณ +/- 2 บนรากที่สองของ n โดยที่ n คือขนาดตัวอย่าง คุณยังสามารถทดสอบอย่างเป็นทางการว่าเป็นไปตามสมมติฐานนี้หรือไม่โดยใช้ การทดสอบ Durbin-Watson
จะทำอย่างไรถ้าสมมติฐานนี้ไม่ได้รับการเคารพ
คุณมีหลายทางเลือก ขึ้นอยู่กับว่าสมมติฐานนี้ถูกละเมิดอย่างไร:
- สำหรับความสัมพันธ์แบบอนุกรมเชิงบวก ให้พิจารณาเพิ่มความล่าช้าของตัวแปรตามและ/หรือตัวแปรอิสระให้กับโมเดล
- สำหรับความสัมพันธ์แบบอนุกรมเชิงลบ ตรวจสอบให้แน่ใจว่าไม่มีตัวแปรใด ล่าช้าเกินไป
- สำหรับความสัมพันธ์ตามฤดูกาล ให้ลองเพิ่มหุ่นตามฤดูกาลให้กับโมเดล
สมมติฐานที่ 3: ความคล้ายคลึงกัน
คำอธิบาย
สมมติฐานถัดไปของการถดถอยเชิงเส้นคือส่วนที่เหลือมีความแปรปรวนคงที่ในแต่ละระดับของ x สิ่งนี้เรียกว่า การรักร่วมเพศ เมื่อไม่เป็นเช่นนั้น สิ่งตกค้างจะประสบกับ ภาวะเฮเทอโรซีดาสติกซิตี
เมื่อมีภาวะเฮเทอโรสซิดาสติกในการวิเคราะห์การถดถอย ผลลัพธ์ของการวิเคราะห์จึงเป็นเรื่องยากที่จะเชื่อได้ โดยเฉพาะอย่างยิ่ง ความแปรปรวนแบบเฮเทอโรสเคดาสติกจะเพิ่มความแปรปรวนของการประมาณค่าสัมประสิทธิ์การถดถอย แต่แบบจำลองการถดถอยไม่ได้คำนึงถึงค่าดังกล่าว ซึ่งทำให้มีโอกาสมากขึ้นที่แบบจำลองการถดถอยจะอ้างว่าคำในแบบจำลองนั้นมีนัยสำคัญทางสถิติ ทั้งที่ในความเป็นจริงกลับไม่มีนัยสำคัญ
จะทราบได้อย่างไรว่าเป็นไปตามสมมติฐานนี้
วิธีที่ง่ายที่สุดในการตรวจจับความแตกต่างแบบเฮเทอโรสเคดาสติกคือการสร้าง ค่าที่พอดี/จุดคงเหลือ
เมื่อคุณปรับเส้นการถดถอยให้พอดีกับชุดข้อมูลแล้ว คุณสามารถสร้างแผนภูมิกระจายที่แสดงค่าที่พอดีของโมเดลเทียบกับค่าที่เหลือของค่าที่พอดีเหล่านั้น แผนภูมิกระจายด้านล่างแสดง แผนภาพทั่วไปของค่าที่พอดีเทียบกับค่าคงเหลือ ซึ่งมีความเป็นเฮเทอโรสเคดาสติกอยู่
สังเกตว่าส่วนที่เหลือจะกระจายออกไปมากขึ้นเรื่อยๆ เมื่อค่าติดตั้งเพิ่มขึ้น รูปร่าง “กรวย” นี้เป็นสัญลักษณ์คลาสสิกของความแตกต่าง:
จะทำอย่างไรถ้าสมมติฐานนี้ไม่ได้รับการเคารพ
มีสามวิธีทั่วไปในการแก้ไขความแตกต่าง:
1. แปลงตัวแปรตาม การแปลงทั่วไปคือเพียงนำบันทึกของตัวแปรตามมา ตัวอย่างเช่น หากเราใช้ขนาดประชากร (ตัวแปรอิสระ) เพื่อทำนายจำนวนร้านดอกไม้ในเมือง (ตัวแปรตาม) เราสามารถลองใช้ขนาดประชากรเพื่อทำนายลอการิทึมของจำนวนร้านดอกไม้ในเมืองแทนได้ การใช้บันทึกของตัวแปรตาม แทนที่จะเป็นตัวแปรตามดั้งเดิม มักจะส่งผลให้ความต่างกันหายไป
2. กำหนดตัวแปรตามใหม่ วิธีทั่วไปในการกำหนดตัวแปรตามใหม่คือการใช้ อัตรา แทนค่าดิบ ตัวอย่างเช่น แทนที่จะใช้ขนาดประชากรเพื่อทำนายจำนวนร้านดอกไม้ในเมือง เราสามารถใช้ขนาดประชากรเพื่อทำนายจำนวนร้านดอกไม้ต่อหัวได้ ในกรณีส่วนใหญ่ สิ่งนี้จะช่วยลดความแปรปรวนที่เกิดขึ้นตามธรรมชาติภายในประชากรจำนวนมากขึ้น เนื่องจากเราวัดจำนวนร้านดอกไม้ต่อคน มากกว่าที่จะวัดจำนวนร้านดอกไม้เอง
3. ใช้การถดถอยแบบถ่วงน้ำหนัก อีกวิธีหนึ่งในการแก้ไขความแตกต่างแบบเฮเทอโรสเคดาสติกคือการใช้การถดถอยแบบถ่วงน้ำหนัก การถดถอยประเภทนี้จะกำหนดน้ำหนักให้กับจุดข้อมูลแต่ละจุดโดยพิจารณาจากความแปรปรวนของค่าที่พอดี โดยพื้นฐานแล้ว สิ่งนี้จะให้น้ำหนักที่ต่ำแก่จุดข้อมูลที่มีความแปรปรวนสูงกว่า ช่วยลดกำลังสองที่เหลือ เมื่อใช้ตุ้มน้ำหนักที่เหมาะสม สิ่งนี้สามารถขจัดปัญหาความไม่สมดุลได้
สมมติฐานที่ 4: ความปกติ
คำอธิบาย
สมมติฐานต่อไปของการถดถอยเชิงเส้นคือส่วนที่เหลือมีการกระจายตามปกติ
จะทราบได้อย่างไรว่าเป็นไปตามสมมติฐานนี้
มีสองวิธีทั่วไปในการตรวจสอบว่าสมมติฐานนี้เป็นไปตามข้อกำหนดหรือไม่:
1. ตรวจสอบสมมติฐานด้วยสายตาโดยใช้ แผน QQ
พล็อต QQ ย่อมาจาก พล็อตควอนไทล์-ควอนไทล์ เป็นพล็อตประเภทหนึ่งที่เราสามารถใช้เพื่อพิจารณาว่าส่วนที่เหลือของแบบจำลองเป็นไปตามการแจกแจงแบบปกติหรือไม่ หากจุดบนโครงเรื่องเป็นเส้นทแยงมุมโดยประมาณ ก็จะถือว่าเป็นไปตามภาวะปกติ
แผนภาพ QQ ต่อไปนี้แสดงตัวอย่างส่วนที่เหลือซึ่งเป็นไปตามการแจกแจงแบบปกติโดยประมาณ:
อย่างไรก็ตาม แผนภาพ QQ ด้านล่างแสดงตัวอย่างกรณีที่สารตกค้างเบี่ยงเบนไปจากเส้นทแยงมุมอย่างชัดเจน ซึ่งบ่งชี้ว่าสิ่งตกค้างไม่เป็นไปตามการแจกแจงแบบปกติ:
2. คุณสามารถตรวจสอบสมมติฐานภาวะปกติได้โดยใช้การทดสอบทางสถิติอย่างเป็นทางการ เช่น Shapiro-Wilk, Kolmogorov-Smironov, Jarque-Barre หรือ D’Agostino-Pearson อย่างไรก็ตาม โปรดทราบว่าการทดสอบเหล่านี้ไวต่อตัวอย่างขนาดใหญ่ กล่าวคือ มักจะสรุปว่าสารตกค้างไม่ปกติเมื่อตัวอย่างของคุณมีขนาดใหญ่ ด้วยเหตุนี้จึงมักจะง่ายกว่าที่จะใช้วิธีการแบบกราฟิก เช่น พล็อต QQ เพื่อยืนยันสมมติฐานนี้
จะทำอย่างไรถ้าสมมติฐานนี้ไม่ได้รับการเคารพ
หากไม่เป็นไปตามสมมติฐานของภาวะปกติ คุณจะมีหลายทางเลือก:
- ขั้นแรก ตรวจสอบว่าค่าผิดปกติไม่มีผลกระทบอย่างมากต่อการกระจาย หากมีค่าผิดปกติตรวจสอบให้แน่ใจว่าเป็นค่าจริงไม่ใช่ข้อผิดพลาดในการป้อนข้อมูล
- จากนั้นคุณสามารถใช้การแปลงแบบไม่เชิงเส้นกับตัวแปรอิสระและ/หรือตัวแปรตามได้ ตัวอย่างทั่วไปได้แก่ การหาบันทึก รากที่สอง หรือส่วนกลับของตัวแปรอิสระและ/หรือตัวแปรตาม
อ่านเพิ่มเติม:
รู้เบื้องต้นเกี่ยวกับการถดถอยเชิงเส้นอย่างง่าย
การทำความเข้าใจเฮเทอโรสเคดาสติกซิตี้ในการวิเคราะห์การถดถอย
วิธีสร้างและตีความพล็อต QQ ใน R