วิธีดำเนินการทดสอบทีสองตัวอย่างใน excel
การทดสอบทีแบบสองตัวอย่าง ใช้เพื่อทดสอบว่าค่าเฉลี่ยของประชากรทั้งสองเท่ากันหรือไม่
บทช่วยสอนนี้จะอธิบายวิธีดำเนินการทดสอบทีสองตัวอย่างใน Excel
วิธีดำเนินการทดสอบทีสองตัวอย่างใน Excel
สมมติว่านักวิจัยต้องการทราบว่าพืชสองชนิดในประเทศที่กำหนดมีความสูงเฉลี่ยเท่ากันหรือไม่ เนื่องจากใช้เวลานานเกินไปในการตรวจวัดแต่ละต้น พวกเขาจึงตัดสินใจเก็บตัวอย่างพืชแต่ละชนิดจำนวน 20 ต้น
รูปภาพต่อไปนี้แสดงความสูง (เป็นนิ้ว) ของแต่ละต้นในแต่ละตัวอย่าง:

เราสามารถทำการทดสอบทีสองตัวอย่างเพื่อตรวจสอบว่าทั้งสองสายพันธุ์มีความสูงเฉลี่ยเท่ากันหรือไม่โดยทำตามขั้นตอนเหล่านี้:
ขั้นตอนที่ 1: พิจารณาว่าความแปรปรวนของประชากรเท่ากันหรือไม่
เมื่อเราทำการทดสอบค่าทีสองตัวอย่าง เราต้องตัดสินใจก่อนว่าเราจะถือว่าประชากรทั้งสองมีความแปรปรวนเท่ากันหรือไม่เท่ากัน โดยทั่วไป เราสามารถสรุปได้ว่าประชากรมีความแปรปรวนเท่ากัน หากอัตราส่วนของความแปรปรวนตัวอย่างที่ใหญ่ที่สุดต่อความแปรปรวนตัวอย่างที่เล็กที่สุดน้อยกว่า 4:1
เราสามารถค้นหาความแปรปรวนสำหรับแต่ละตัวอย่างได้โดยใช้ฟังก์ชัน Excel =VAR.S(Cell range) ดังที่แสดงในรูปภาพต่อไปนี้:
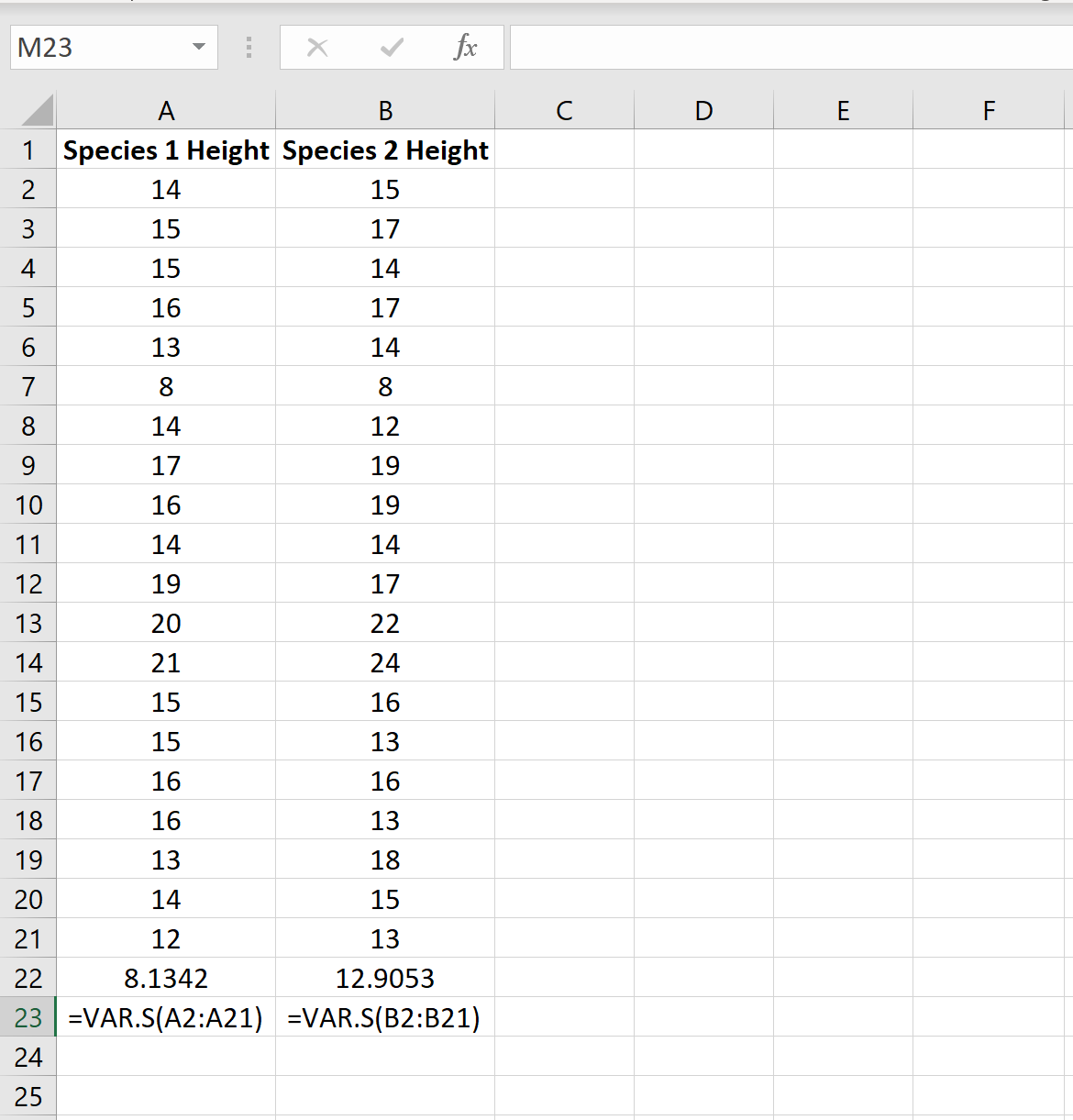
อัตราส่วนของความแปรปรวนตัวอย่างที่ใหญ่ที่สุดต่อความแปรปรวนตัวอย่างที่น้อยที่สุดคือ 12.9053/8.1342 = 1.586 ซึ่งน้อยกว่า 4 ซึ่งหมายความว่าเราสามารถสรุปได้ว่าความแปรปรวนของประชากรเท่ากัน
ขั้นตอนที่ 2: เปิด Analysis ToolPak
ในแท็บข้อมูลของ Ribbon ด้านบน คลิก “การวิเคราะห์ข้อมูล”

หากคุณไม่เห็นตัวเลือกนี้ให้คลิก คุณต้อง ดาวน์โหลด Analysis ToolPak ซึ่งไม่มีค่าใช้จ่ายใดๆ ทั้งสิ้น
ขั้นตอนที่ 3: เลือกการทดสอบที่เหมาะสมที่จะใช้
เลือกตัวเลือกที่ระบุว่า t-test: สองตัวอย่างถือว่าความแปรปรวนเท่ากัน แล้วคลิกตกลง
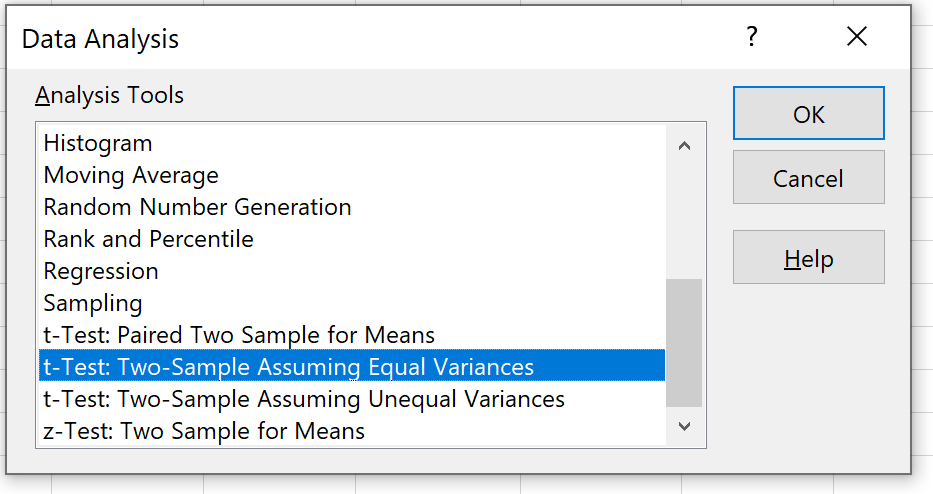
ขั้นตอนที่ 4: ป้อนข้อมูลที่จำเป็น
ป้อนช่วงของค่าสำหรับตัวแปร 1 (ตัวอย่างแรกของเรา), ตัวแปร 2 (ตัวอย่างที่สองของเรา), ผลต่างค่าเฉลี่ยสมมุติ (ในกรณีนี้เราใส่ “0” เพราะเราต้องการทราบว่าผลต่างของประชากรที่แท้จริงคือ 0 หรือไม่) และช่วงเอาท์พุตที่เราต้องการเห็นผลการทดสอบทีแสดงขึ้น จากนั้นคลิกตกลง

ขั้นตอนที่ 5: ตีความผลลัพธ์
เมื่อคุณคลิกตกลงในขั้นตอนก่อนหน้า ผลการทดสอบทีจะแสดงขึ้น

ต่อไปนี้เป็นวิธีการตีความผลลัพธ์:
ค่าเฉลี่ย: นี่คือค่าเฉลี่ยของแต่ละตัวอย่าง ตัวอย่างที่ 1 มีความสูงเฉลี่ย 15.15 และตัวอย่างที่ 2 มีความสูงเฉลี่ย 15.8
ความแปรปรวน: นี่คือความแปรปรวนสำหรับแต่ละตัวอย่าง ตัวอย่างที่ 1 มีความแปรปรวน 8.13 และตัวอย่างที่ 2 มีความแปรปรวน 12.90
การสังเกต: นี่คือจำนวนการสังเกตในแต่ละตัวอย่าง ตัวอย่างทั้งสองมีการสังเกต 20 รายการ (เช่น พืช 20 ต้นในแต่ละตัวอย่าง)
ความแปรปรวนรวม: ตัวเลขที่คำนวณโดย “การรวมกลุ่ม” ความแปรปรวนของแต่ละตัวอย่างโดยใช้สูตร s 2 p = [ (n 1 -1)s 2 1 + (n 2 -1)s 2 2 ] / (n 1 +n 2 – 2) ซึ่งกลายเป็น 10.51974 จากนั้นจะใช้ตัวเลขนี้ในการคำนวณสถิติ t -test
ความแตกต่างเฉลี่ยสมมุติ: จำนวนที่เรา “ตั้งสมมติฐาน” คือความแตกต่างระหว่างค่าเฉลี่ยของประชากรทั้งสอง ในกรณีนี้ เราเลือก 0 เพราะเราต้องการทดสอบว่าความแตกต่างระหว่างค่าเฉลี่ยของประชากรทั้งสองมีค่าเท่ากับ 0 หรือไม่ เช่น ไม่มีความแตกต่างกัน
df: องศาอิสระสำหรับการทดสอบที คำนวณเป็น n 1 + n 2 -2 = 20 + 20 – 2 = 38
t Stat: สถิติการทดสอบ t คำนวณเป็น t = [ x 1 – x 2 ] / √ [s 2 p (1/n 1 + 1/n 2 )]
ในกรณีนี้ t = [15.15-15.8] / √ [10.51974(1/20+1/20)] = -0.63374 .
P แบบสองด้าน(T<=t): ค่า p สำหรับการทดสอบแบบสองด้าน ในกรณีนี้ p = 0.530047 . ซึ่งมากกว่าอัลฟ่า = 0.05 มาก ดังนั้นเราจึงไม่สามารถปฏิเสธสมมติฐานว่างได้ เราไม่มีหลักฐานเพียงพอที่จะบอกว่าค่าเฉลี่ยของประชากรทั้งสองแตกต่างกัน
ค่าวิกฤตแบบสองด้าน: นี่คือค่าวิกฤตของการทดสอบ ซึ่งพบได้จากการระบุค่าในตารางการแจกแจงแบบ t ที่สอดคล้องกับการทดสอบแบบสองด้านโดยมีค่า alpha = 0.05 และ df = 38 ซึ่งกลายเป็น 2 024394 . เนื่องจากสถิติการทดสอบ ที ของเราน้อยกว่าค่านี้ เราจึงปฏิเสธสมมติฐานว่างไม่ได้ เราไม่มีหลักฐานเพียงพอที่จะบอกว่าค่าเฉลี่ยของประชากรทั้งสองแตกต่างกัน
โปรดทราบว่าทั้งวิธีค่า p และค่าวิกฤตจะนำไปสู่ข้อสรุปเดียวกัน
แหล่งข้อมูลเพิ่มเติม
บทช่วยสอนต่อไปนี้จะอธิบายวิธีการทดสอบทีประเภทอื่นๆ ใน Excel:
วิธีดำเนินการทดสอบทีตัวอย่างเดียวใน Excel
วิธีดำเนินการทดสอบตัวอย่างแบบจับคู่ใน Excel