วิธีการคำนวณค่าสัมประสิทธิ์สหสัมพันธ์เพียร์สันด้วยตนเอง

ค่าสัมประสิทธิ์สหสัมพันธ์แบบเพียร์สัน วัดความสัมพันธ์เชิงเส้นระหว่างตัวแปรสองตัว

จะใช้ค่าระหว่าง -1 ถึง 1 เสมอโดยที่:

• -1 บ่งชี้ถึงความสัมพันธ์เชิงเส้นเชิงลบอย่างสมบูรณ์ระหว่างตัวแปรสองตัว
• 0 บ่งชี้ว่าไม่มีความสัมพันธ์เชิงเส้นระหว่างตัวแปรสองตัว
• 1 บ่งชี้ความสัมพันธ์เชิงเส้นเชิงบวกอย่างสมบูรณ์ระหว่างตัวแปรสองตัว

สูตรในการคำนวณค่าสัมประสิทธิ์สหสัมพันธ์แบบเพียร์สัน แทนด้วย r คือ:

บทช่วยสอนนี้ให้ตัวอย่างทีละขั้นตอนของวิธีคำนวณค่าสัมประสิทธิ์สหสัมพันธ์แบบเพียร์สันด้วยตนเองสำหรับชุดข้อมูลต่อไปนี้:

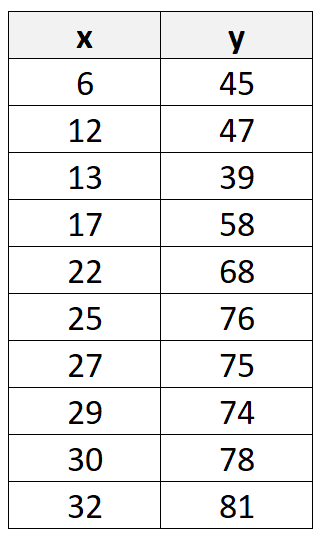
ขั้นตอนที่ 1: คำนวณค่าเฉลี่ยของ X และ Y

ขั้นแรก เราจะคำนวณค่าเฉลี่ยของค่า X และ Y:

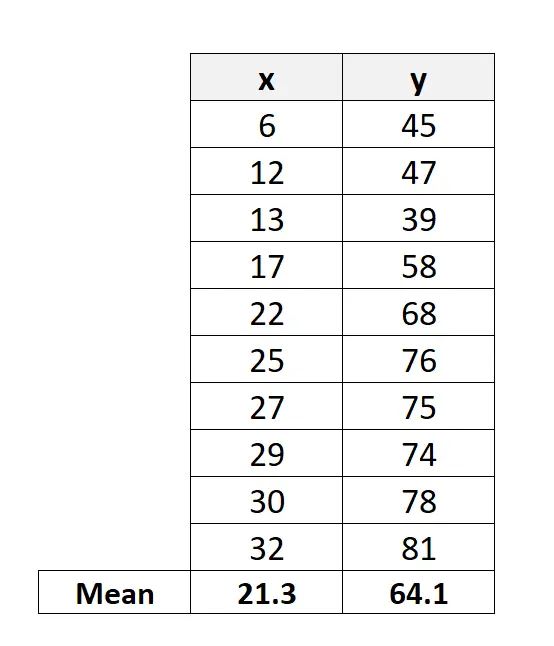
ขั้นตอนที่ 2: คำนวณความแตกต่างระหว่างค่าเฉลี่ย

ต่อไปเราจะคำนวณความแตกต่างระหว่างแต่ละค่า X และ Y และวิธีการตามลำดับ:

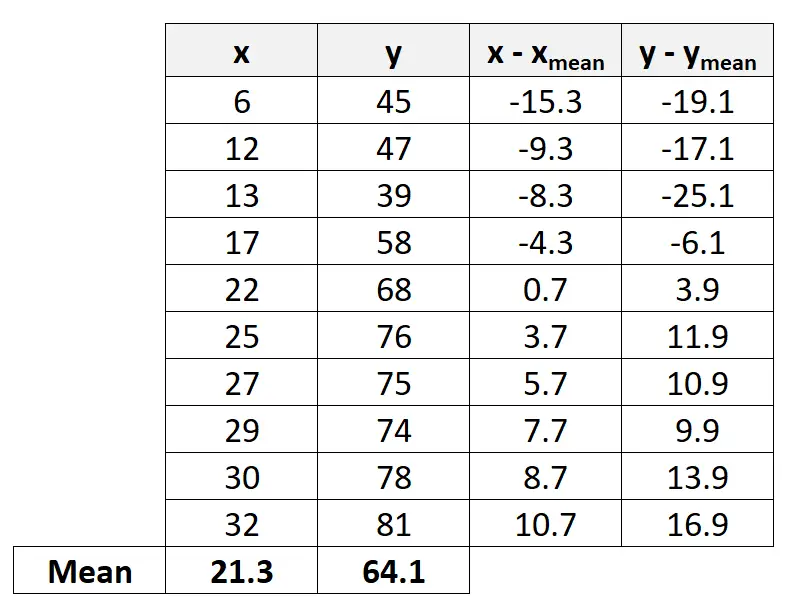
ขั้นตอนที่ 3: คำนวณค่าที่เหลือ

ต่อไปเราจะคำนวณค่าที่เหลือที่จำเป็นในการกรอกสูตรสัมประสิทธิ์สหสัมพันธ์ของเพียร์สัน:

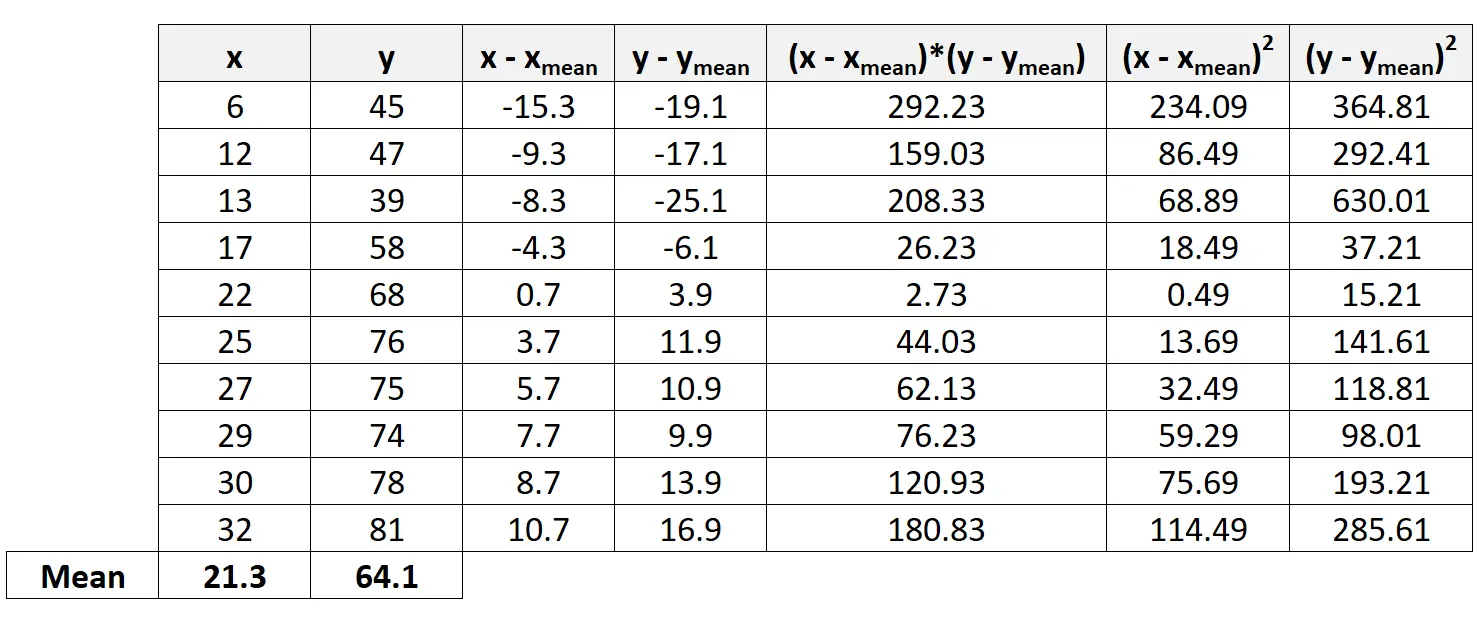
ขั้นตอนที่ 4: คำนวณผลรวม

ต่อไป เราจะคำนวณผลรวมของสามคอลัมน์สุดท้าย:

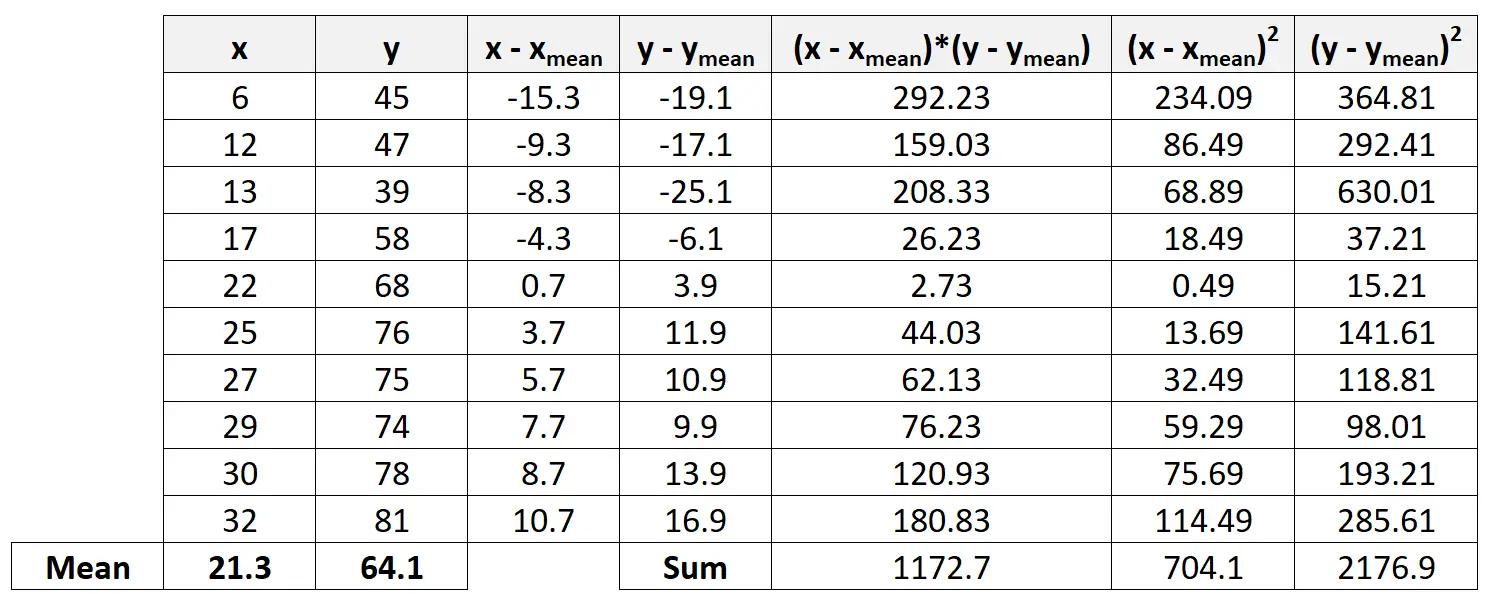
ขั้นตอนที่ 5: คำนวณค่าสัมประสิทธิ์สหสัมพันธ์เพียร์สัน

ตอนนี้เราจะแทนผลรวมจากขั้นตอนที่แล้วลงในสูตรสัมประสิทธิ์สหสัมพันธ์แบบเพียร์สัน:

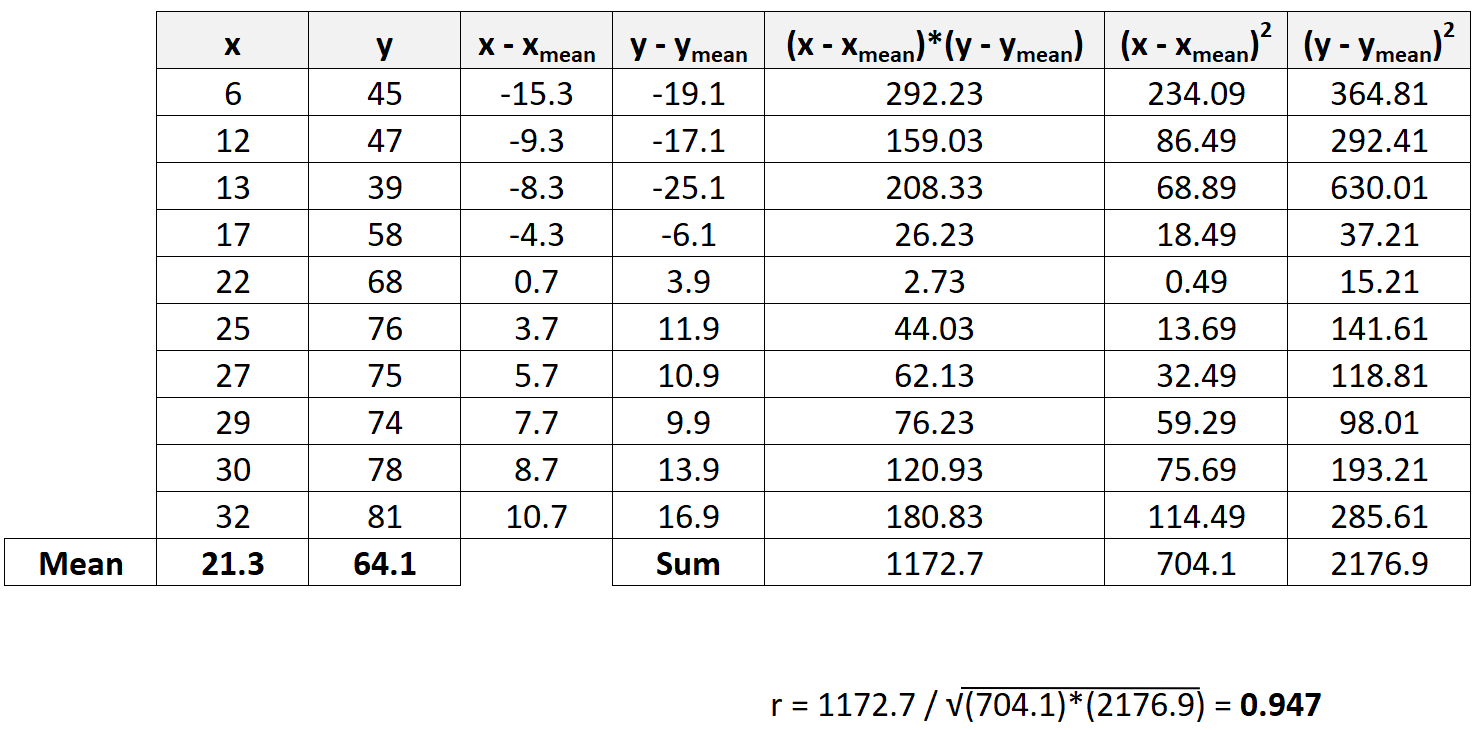
ค่าสัมประสิทธิ์สหสัมพันธ์เพียร์สันกลายเป็น 0.947

เนื่องจากค่านี้ใกล้กับ 1 จึงบ่งชี้ว่า X และ Y มีความสัมพันธ์เชิงบวกอย่างมาก

กล่าวอีกนัยหนึ่ง เมื่อค่าของ X เพิ่มขึ้น ค่าของ Y ก็จะเพิ่มขึ้นในลักษณะที่สามารถคาดเดาได้สูงเช่นกัน

แหล่งข้อมูลเพิ่มเติม

ความรู้เบื้องต้นเกี่ยวกับสัมประสิทธิ์สหสัมพันธ์เพียร์สัน
วิธีค้นหาช่วงความเชื่อมั่นของค่าสัมประสิทธิ์สหสัมพันธ์