สารตกค้างในสถิติคืออะไร?

คงเหลือ คือความแตกต่างระหว่างค่าที่สังเกตได้และค่าที่คาดการณ์ไว้ใน การวิเคราะห์การถดถอย

มีการคำนวณดังนี้:

คงเหลือ = ค่าที่สังเกตได้ – ค่าที่คาดการณ์ไว้

โปรดจำไว้ว่าเป้าหมายของการถดถอยเชิงเส้นคือการหาปริมาณความสัมพันธ์ระหว่างตัวแปรทำนายตั้งแต่หนึ่งตัวขึ้นไปกับ ตัวแปรตอบสนอง เมื่อต้องการทำเช่นนี้ การถดถอยเชิงเส้นจะค้นหาเส้นที่ “พอดี” กับข้อมูลมากที่สุด ซึ่งเรียกว่า เส้นการถดถอยกำลังสองน้อยที่สุด

เส้นนี้สร้างคำทำนายสำหรับ การสังเกต แต่ละครั้งในชุดข้อมูล แต่ไม่น่าเป็นไปได้ที่การทำนายที่ทำโดยเส้นการถดถอยจะ ตรง กับค่าที่สังเกตได้ทุกประการ

ความแตกต่างระหว่างการทำนายและค่าที่สังเกตได้คือค่าคงเหลือ หากเราพล็อตค่าที่สังเกตได้และวางทับเส้นการถดถอยที่ติดตั้งไว้ ยอดคงเหลือสำหรับการสังเกตแต่ละครั้งจะเป็นระยะห่างแนวตั้งระหว่างการสังเกตและเส้นการถดถอย:

การสังเกตจะมีค่า คงเหลือเป็นบวก ถ้าค่าของมันมากกว่าค่าที่ทำนายไว้โดยเส้นการถดถอย

ในทางกลับกัน การสังเกตจะมีค่า คงเหลือเป็นลบ หากค่าของมันน้อยกว่าค่าที่ทำนายไว้โดยเส้นการถดถอย

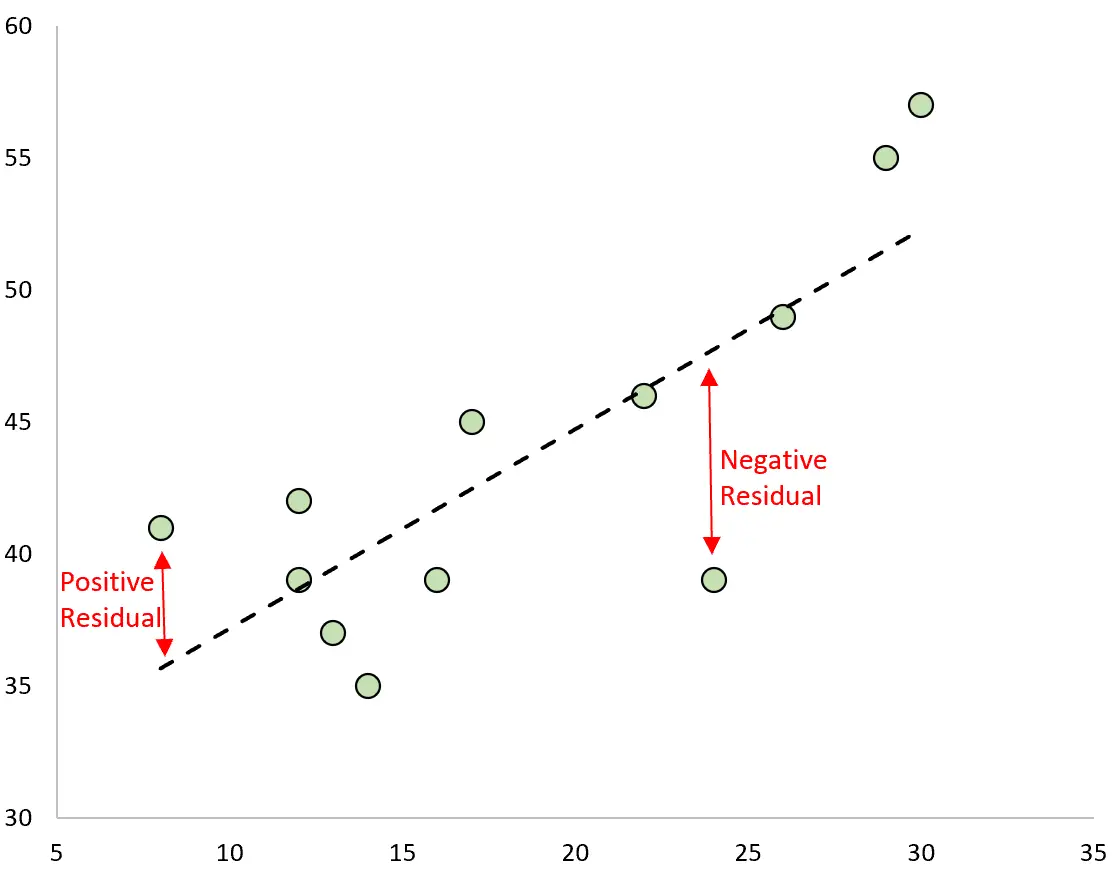
การสังเกตบางอย่างจะมีค่าตกค้างเป็นบวก ในขณะที่บางค่าจะมีค่าตกค้างเป็นลบ แต่ค่าตกค้างทั้งหมดจะรวมกัน เป็นศูนย์

ตัวอย่างการคำนวณยอดคงเหลือ

สมมติว่าเรามีชุดข้อมูลต่อไปนี้ซึ่งมีการสังเกตทั้งหมด 12 รายการ:

หากเราใช้ซอฟต์แวร์ทางสถิติ (เช่น R , Excel , Python , Stata ฯลฯ) เพื่อให้พอดีกับเส้นการถดถอยเชิงเส้นกับชุดข้อมูลนี้ เราจะพบว่าเส้นที่เหมาะสมที่สุดกลายเป็น:

y = 29.63 + 0.7553x

เมื่อใช้เส้นนี้ เราสามารถคำนวณค่าที่ทำนายไว้สำหรับค่า Y แต่ละค่าตามค่าของ X ตัวอย่างเช่น ค่าที่ทำนายของการสังเกตครั้งแรกจะเป็น:

y = 29.63 + 0.7553*(8) = 35.67

จากนั้นเราสามารถคำนวณค่าคงเหลือสำหรับการสังเกตนี้ได้ดังนี้:

คงเหลือ = ค่าที่สังเกตได้ – ค่าที่คาดการณ์ = 41 – 35.67 = 5.33

เราสามารถทำซ้ำขั้นตอนนี้เพื่อค้นหาสิ่งตกค้างสำหรับการสังเกตแต่ละครั้ง:

หากเราสร้างแผนภาพกระจายเพื่อแสดงภาพการสังเกตด้วยเส้นการถดถอยที่พอดี เราจะเห็นว่าการสังเกตบางส่วนอยู่เหนือเส้น ในขณะที่บางจุดอยู่ใต้เส้น:

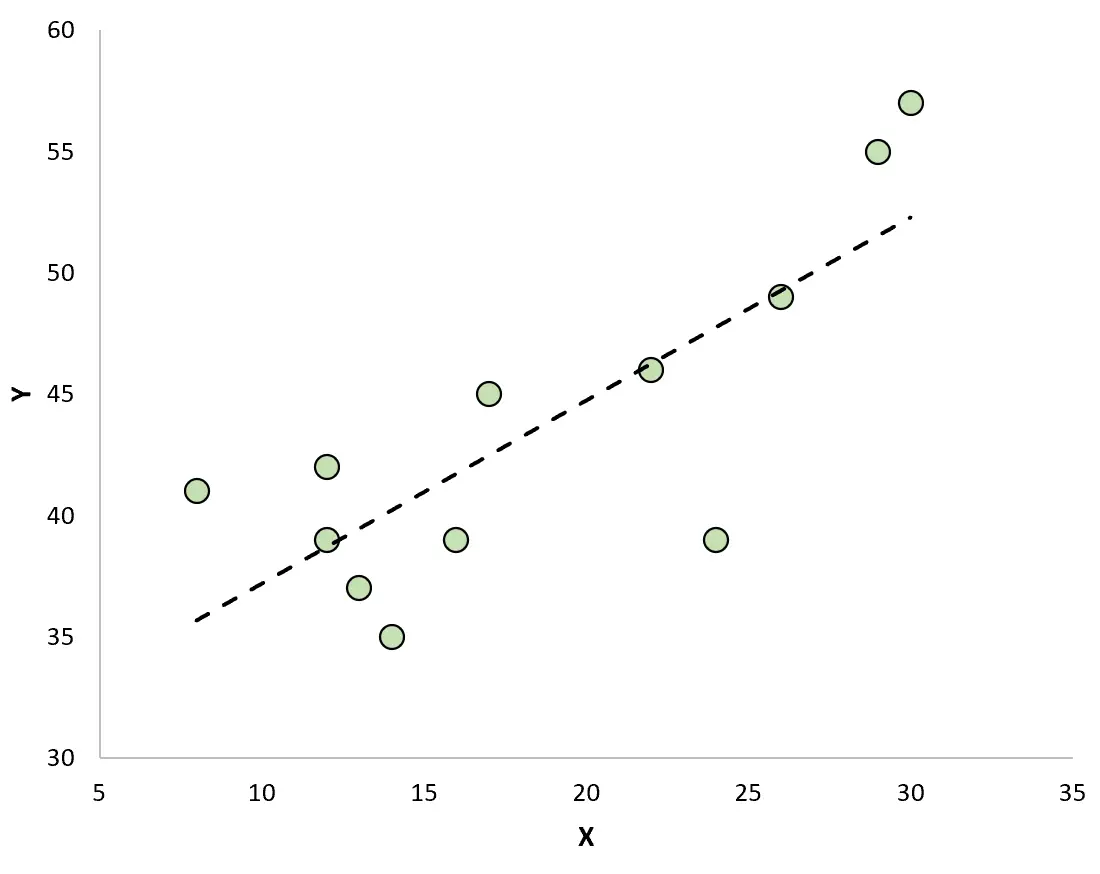
คุณสมบัติของสารตกค้าง

สารตกค้างมีคุณสมบัติดังต่อไปนี้:

• การสังเกตแต่ละครั้งในชุดข้อมูลจะมีค่าคงเหลือที่สอดคล้องกัน ดังนั้น หากชุดข้อมูลประกอบด้วยการสังเกตทั้งหมด 100 ครั้ง แบบจำลองจะสร้างค่าที่คาดการณ์ไว้ 100 ค่า ส่งผลให้มีค่าคงเหลือทั้งหมด 100 ค่า
• ผลรวมของยอดคงเหลือทั้งหมดเป็นศูนย์
• มูลค่าเฉลี่ยของปริมาณคงเหลือเป็นศูนย์

สารตกค้างถูกนำมาใช้ในทางปฏิบัติอย่างไร?

ในทางปฏิบัติ สารตกค้างจะถูกใช้ด้วยเหตุผลสามประการในการถดถอย:

1. ประเมินความเพียงพอของแบบจำลอง

เมื่อเราสร้างเส้นการถดถอยพอดีแล้ว เราก็สามารถคำนวณ ผลรวมของกำลังสองที่เหลือ (RSS) ซึ่งเป็นผลรวมของกำลังสองที่เหลือทั้งหมด ยิ่ง RSS ต่ำ โมเดลการถดถอยจะเข้ากับข้อมูลได้ดียิ่งขึ้น

2. ตรวจสอบสมมติฐานปกติ

ข้อสันนิษฐานสำคัญประการหนึ่งของการถดถอยเชิงเส้น คือส่วนที่เหลือมีการกระจายตามปกติ

เพื่อทดสอบสมมติฐานนี้ เราสามารถสร้างพล็อต QQ ซึ่งเป็นประเภทของพล็อตที่เราสามารถใช้เพื่อพิจารณาว่าส่วนที่เหลือของแบบจำลองเป็นไปตามการแจกแจงแบบปกติหรือไม่

หากจุดบนโครงเรื่องเป็นเส้นทแยงมุมโดยประมาณ ก็จะถือว่าเป็นไปตามภาวะปกติ

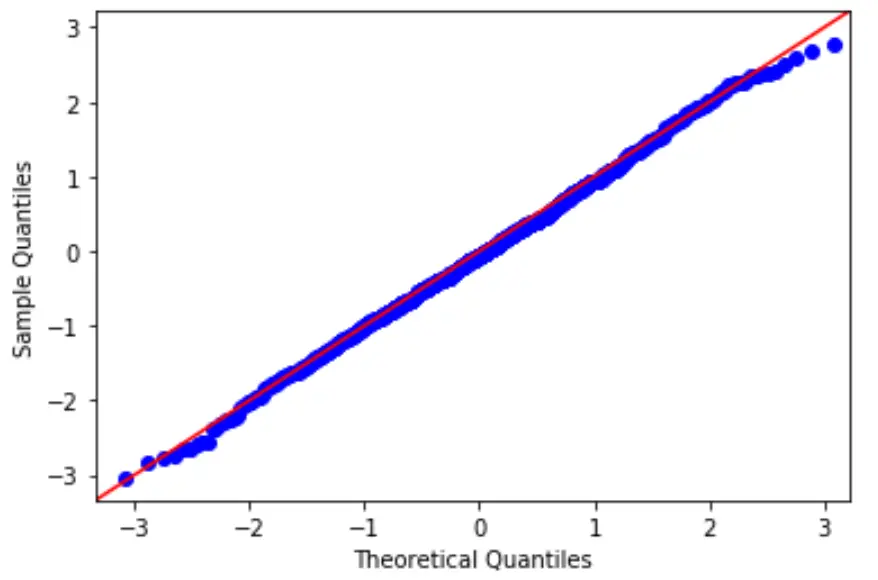
3. ตรวจสอบสมมติฐานความเป็นเนื้อเดียวกัน

สมมติฐานที่สำคัญอีกประการหนึ่งของการถดถอยเชิงเส้นคือส่วนที่เหลือมีความแปรปรวนคงที่ในแต่ละระดับของ x สิ่งนี้เรียกว่าการรักร่วมเพศ เมื่อไม่เป็นเช่นนั้น สิ่งตกค้างจะประสบกับ ภาวะเฮเทอโรซีดาสติกซิตี

เพื่อตรวจสอบว่าเป็นไปตามสมมติฐานนี้หรือไม่ เราสามารถสร้าง จุดคงเหลือ ซึ่งเป็นแผนภาพกระจายที่แสดงค่าคงเหลือเทียบกับค่าที่คาดการณ์ไว้ของแบบจำลอง

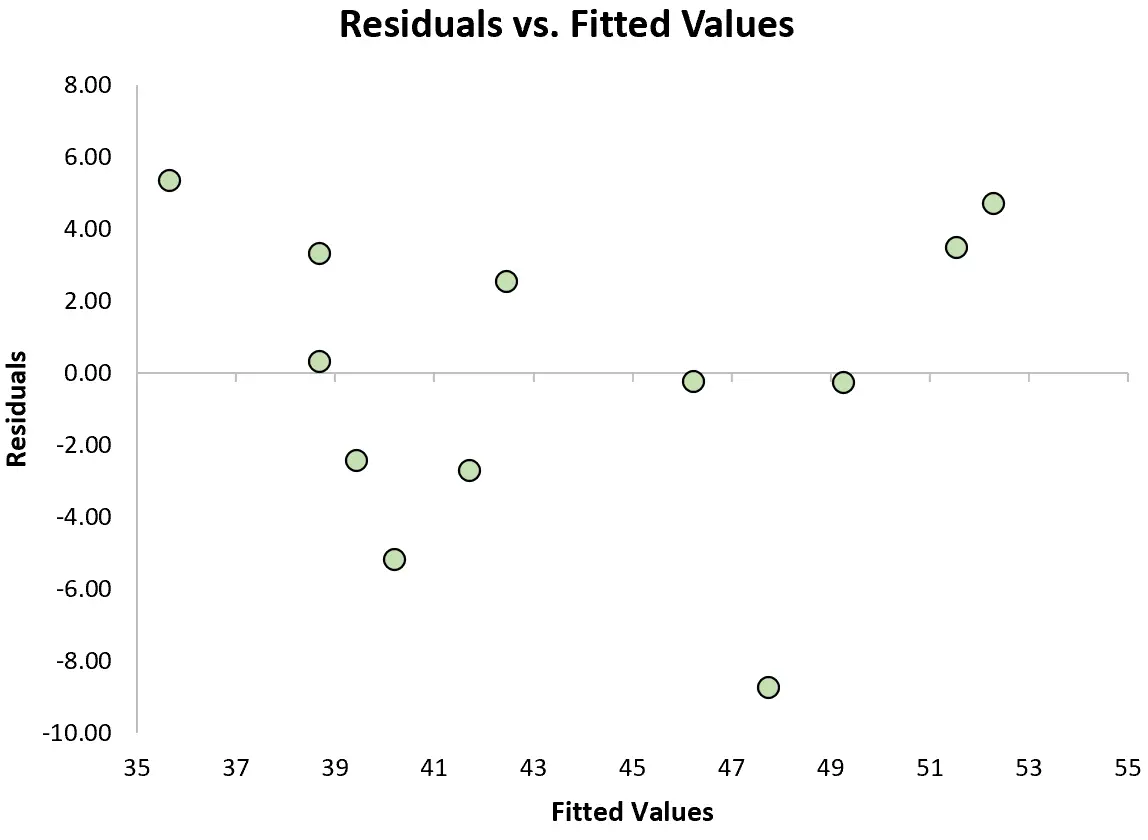
ถ้าส่วนที่เหลือมีการกระจายเท่าๆ กันประมาณประมาณศูนย์ในกราฟโดยไม่มีแนวโน้มที่ชัดเจน โดยทั่วไปแล้วเราจะกล่าวว่าเป็นไปตามสมมติฐานของความเป็นเนื้อเดียวกัน

แหล่งข้อมูลเพิ่มเติม

รู้เบื้องต้นเกี่ยวกับการถดถอยเชิงเส้นอย่างง่าย
รู้เบื้องต้นเกี่ยวกับการถดถอยเชิงเส้นพหุคูณ
สมมติฐานสี่ประการของการถดถอยเชิงเส้น
วิธีการสร้างพล็อตที่เหลือใน Excel