ส่วนเบี่ยงเบนมาตรฐาน (หรือส่วนเบี่ยงเบนมาตรฐาน)

โดย ดร.เบนจามิน แอนเดอร์สัน สิงหาคม 5, 2023 สถิติ 0 ความคิดเห็น

บทความนี้จะอธิบายว่าค่าเบี่ยงเบนมาตรฐานหรือที่เรียกว่าค่าเบี่ยงเบนมาตรฐานคืออะไร คุณจะได้เรียนรู้วิธีการคำนวณค่าเบี่ยงเบนมาตรฐาน ตัวอย่างเชิงปฏิบัติทีละขั้นตอน และเครื่องคำนวณออนไลน์เพื่อค้นหาค่าเบี่ยงเบนมาตรฐานของตัวอย่างข้อมูลใดๆ

ค่าเบี่ยงเบนมาตรฐาน (หรือค่าเบี่ยงเบนมาตรฐาน) คืออะไร?

ส่วนเบี่ยงเบนมาตรฐาน หรือที่เรียกว่า ส่วนเบี่ยงเบนมาตรฐาน เป็นการวัดการกระจายตัวทางสถิติ กล่าวอีกนัยหนึ่ง ค่าเบี่ยงเบนมาตรฐานคือค่าที่ระบุการกระจายตัวของชุดข้อมูลทางสถิติ

ดังนั้น ค่าเบี่ยงเบนมาตรฐาน (หรือค่าเบี่ยงเบนมาตรฐาน) จึงถูกนำมาใช้เพื่อหาปริมาณการกระจายตัวของประชากรหรือตัวอย่างทางสถิติ ยิ่งค่าเบี่ยงเบนมาตรฐานของชุดข้อมูลมากเท่าใด ข้อมูลก็จะยิ่งกระจัดกระจายมากขึ้นเท่านั้น และการตีความก็สามารถทำได้ในทิศทางอื่นเช่นกัน หากค่าเบี่ยงเบนมาตรฐานต่ำ หมายความว่าข้อมูลโดยทั่วไปใกล้เคียงกับค่าเฉลี่ยมาก

เมื่อคำนวณค่ามาตรฐานหรือค่าเบี่ยงเบนทั่วไปของประชากร สัญลักษณ์ของค่าเบี่ยงเบนมาตรฐาน คืออักษรกรีก sigma (σ) แต่เมื่อพูดถึงค่าเบี่ยงเบนมาตรฐานของกลุ่มตัวอย่าง ตัวอักษร s จะใช้แทนการวัดทางสถิติ

ในหนังสือสถิติและความน่าจะเป็นบางเล่ม ค่าเบี่ยงเบนมาตรฐานเรียกอีกอย่างว่าค่าเบี่ยงเบนมาตรฐาน

สูตรค่าเบี่ยงเบนมาตรฐาน (หรือค่าเบี่ยงเบนมาตรฐาน)

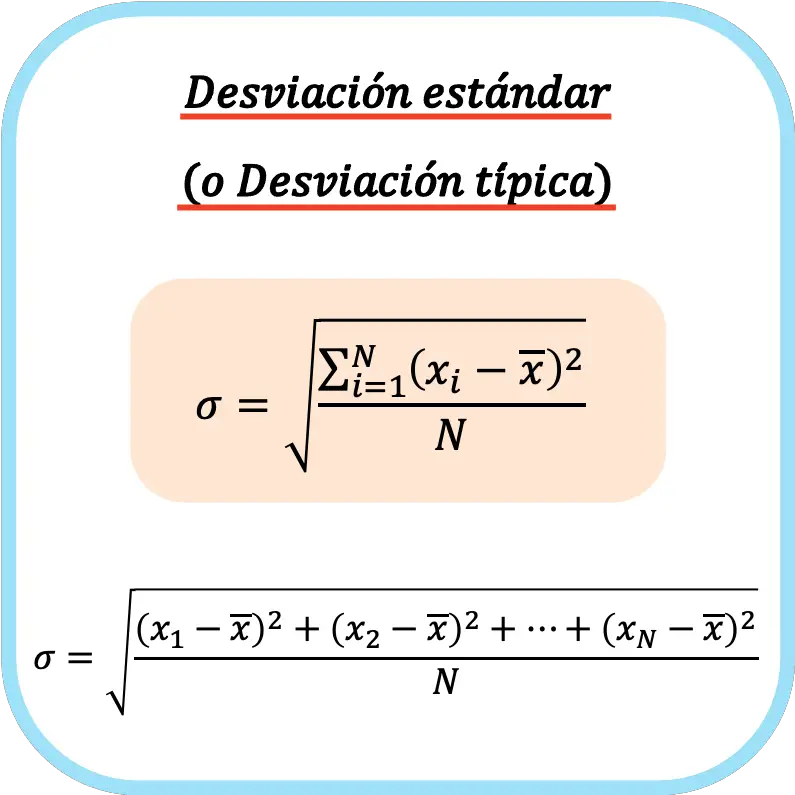
ค่าเบี่ยงเบนมาตรฐาน (หรือค่าเบี่ยงเบนมาตรฐาน) เท่ากับรากที่สองของผลรวมของกำลังสองของค่าเบี่ยงเบนของชุดข้อมูลหารด้วยจำนวนการสังเกตทั้งหมด

สูตรในการคำนวณค่าเบี่ยงเบนมาตรฐาน (หรือค่าเบี่ยงเบนมาตรฐาน) จึงเป็นดังนี้:

ส่วนเบี่ยงเบนมาตรฐาน ส่วนเบี่ยงเบนมาตรฐาน

👉 คุณสามารถใช้เครื่องคิดเลขด้านล่างเพื่อคำนวณค่าเบี่ยงเบนมาตรฐานของชุดข้อมูลใดก็ได้

โดยสรุป ในการค้นหาค่าเบี่ยงเบนมาตรฐานของชุดข้อมูล คุณจะต้องคำนวณค่าเบี่ยงเบนทั้งหมด (ซึ่งหมายถึงความแตกต่างระหว่างจุดข้อมูลและค่าเฉลี่ยเลขคณิต) เพิ่มค่าเบี่ยงเบนเป็น 2 แล้วบวกทั้งหมดเข้าด้วยกัน จากนั้นหารด้วย ทั้งหมด. จำนวนข้อมูล และสุดท้ายก็หาค่ารากที่สอง

ตัวอย่างค่าเบี่ยงเบนมาตรฐาน (หรือค่าเบี่ยงเบนมาตรฐาน)

เมื่อพิจารณาคำจำกัดความของค่าเบี่ยงเบนมาตรฐาน (หรือค่าเบี่ยงเบนทั่วไป) ด้านล่างนี้คือตัวอย่างทีละขั้นตอน เพื่อให้คุณสามารถดูวิธีคำนวณค่าเบี่ยงเบนมาตรฐานของชุดข้อมูลได้

คำนวณค่าเบี่ยงเบนมาตรฐานของค่าต่อไปนี้: 3, 6, 2, 9, 4

สิ่งแรกที่เราต้องทำคือหาค่าเฉลี่ยตัวอย่าง ในการดำเนินการนี้ เราจะบวกข้อมูลทั้งหมดและหารด้วยจำนวนการสังเกตทั้งหมด ซึ่งก็คือ 5:

$\overline{x}=\cfrac{3+6+2+9+4}{5}=4,8$

ตอนนี้เราใช้สูตรค่าเบี่ยงเบนมาตรฐาน:

$\displaystyle\sigma=\sqrt{\frac{\displaystyle\sum_{i=1}^N(x_i-\overline{x})^2}{N}}$

เราแทนที่ข้อมูลลงในสูตร:

$\displaystyle\sigma =\sqrt{\frac{(3-4,8)^2+(6-4,8)^2+(2-4,8)^2+(9-4,8)^2+(4-4,8)^2}{5}}$

และสุดท้าย เราก็คำนวณค่าเบี่ยงเบนมาตรฐาน:

$\begin{aligned}\displaystyle\sigma & = \sqrt{\frac{(-1,8)^2+1,2^2+(-2,8)^2+4,2^2+(-0,8)^2}{5}}\\[2ex]&=\sqrt{\frac{3,24+1,44+7,84+17,64+0,64}{5}}\\[2ex]&= \sqrt{\frac{30,8}{5}}=\sqrt{6,16}=2,48 \end{aligned}$

เครื่องคิดเลขค่าเบี่ยงเบนมาตรฐาน (หรือค่าเบี่ยงเบนมาตรฐาน)

ใส่ชุดข้อมูลทางสถิติลงในเครื่องคิดเลขออนไลน์ต่อไปนี้เพื่อคำนวณค่าเบี่ยงเบนมาตรฐาน (หรือค่าเบี่ยงเบนมาตรฐาน) ข้อมูลต้องคั่นด้วยช่องว่างและป้อนโดยใช้จุดเป็นตัวคั่นทศนิยม

ค่าเบี่ยงเบนมาตรฐาน (หรือทั่วไป) สำหรับข้อมูลที่จัดกลุ่ม

ในการคำนวณค่าเบี่ยงเบนมาตรฐาน (หรือค่าเบี่ยงเบนมาตรฐาน) ของข้อมูลที่จัดกลุ่มตามช่วงเวลา ต้องปฏิบัติตามขั้นตอนต่อไปนี้:

ค้นหาค่าเฉลี่ยของข้อมูลที่จัดกลุ่ม
คำนวณความเบี่ยงเบนของข้อมูลที่จัดกลุ่ม
ตารางแต่ละช่องว่าง
คูณผลลัพธ์ก่อนหน้าแต่ละรายการด้วยความถี่ของช่วงเวลา
เพิ่มผลรวมของค่าทั้งหมดที่ได้รับในขั้นตอนก่อนหน้า
หารด้วยจำนวนการสังเกตทั้งหมด
หารากที่สองของค่าก่อนหน้า จำนวนผลลัพธ์คือค่าเบี่ยงเบนมาตรฐานของข้อมูลที่จัดกลุ่ม

โดยสรุป สูตรในการคำนวณค่าเบี่ยงเบนมาตรฐานของข้อมูลที่จัดกลุ่มเป็นช่วงๆ คือ

$\displaystyle\sigma=\sqrt{\frac{\displaystyle\sum_{i=1}^N\left(x_i-\overline{x}\right)^2\cdot f_i }{N}}$

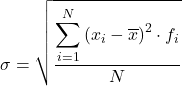
แม้ว่าปกติจะใช้สูตรข้างต้น แต่ก็สามารถใช้นิพจน์พีชคณิตต่อไปนี้ได้เนื่องจากได้ผลลัพธ์เดียวกัน:

$\displaystyle\sigma=\sqrt{\frac{\displaystyle\sum_{i=1}^n x_i^2\cdot f_i }{N}-\overline{x}^2}$

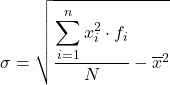
คุณจะเห็นวิธีการทำ ด้านล่างนี้คือแบบฝึกหัดทีละขั้นตอนเกี่ยวกับค่าเบี่ยงเบนมาตรฐานของข้อมูลที่จัดกลุ่มตามช่วงต่างๆ แม่นยำยิ่งขึ้นคือค่าเบี่ยงเบนมาตรฐานของข้อมูลทางสถิติต่อไปนี้จะถูกคำนวณ:

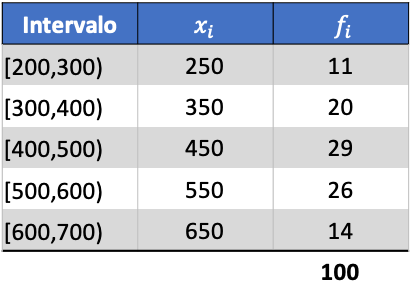
ขั้นแรก เราจะคูณคะแนนชั้นเรียนของแต่ละช่วงเวลาด้วยความถี่เพื่อคำนวณค่าเฉลี่ยเลขคณิต:

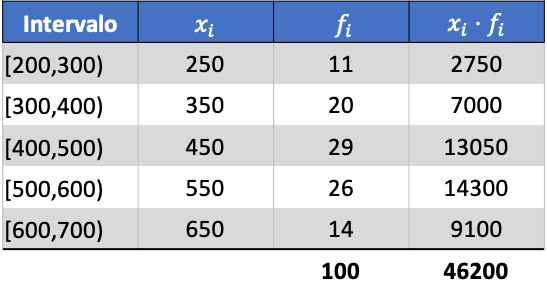
ดังนั้นค่าเฉลี่ยของข้อมูลที่จัดกลุ่มจะเป็น:

$\overline{x}=\cfrac{\displaystyle\sum_{i=1}^n x_i\cdot f_i}{N}=\cfrac{46200}{100}=462$

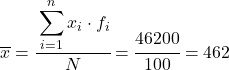
ตอนนี้เราทราบค่าของค่าเฉลี่ยแล้ว เราต้องเพิ่มคอลัมน์สามคอลัมน์ต่อไปนี้ลงในตารางข้อมูล:

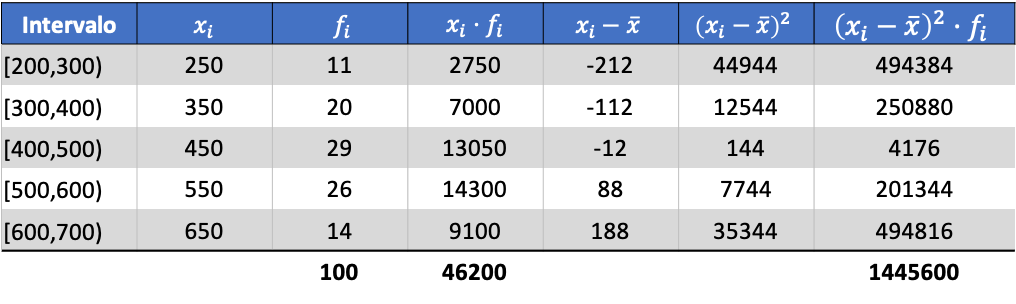
แก้การใช้ค่าเบี่ยงเบนมาตรฐานหรือค่าเบี่ยงเบนมาตรฐานสำหรับข้อมูลที่จัดกลุ่ม

จากนั้น ค่าเบี่ยงเบนมาตรฐานของข้อมูลที่จัดกลุ่มจะเป็นผลลัพธ์ของรากที่สองของผลรวมของคอลัมน์สุดท้ายหารด้วยจำนวนการสังเกตทั้งหมด:

$\displaystyle\sigma=\sqrt{\frac{\displaystyle\sum_{i=1}^N\left(x_i-\overline{x}\right)^2\cdot f_i }{N}}=\sqrt{\frac{1445600}{100}}=120,23$

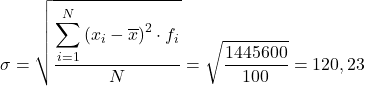
ค่าเบี่ยงเบนมาตรฐาน (หรือทั่วไป) และความแปรปรวน

ความสัมพันธ์ระหว่างค่าเบี่ยงเบนมาตรฐาน (หรือค่าเบี่ยงเบนทั่วไป) และความแปรปรวน คือค่าเบี่ยงเบนมาตรฐานคือรากที่สองของความแปรปรวน

ดังนั้น ถ้าเราทราบค่าความแปรปรวนของชุดข้อมูล เราก็สามารถคำนวณค่าเบี่ยงเบนมาตรฐานได้อย่างง่ายดายโดยการหารากที่สอง หรือในทางกลับกัน ถ้าเรารู้ค่าเบี่ยงเบนมาตรฐาน เราก็สามารถหาความแปรปรวนได้โดยการยกกำลังสองค่า

$Var(X)=\sigma^2$

ที่จริงแล้ว ความแปรปรวนสามารถแสดงได้ง่ายๆ โดยใช้สัญลักษณ์ส่วนเบี่ยงเบนมาตรฐานกำลังสอง ดังนั้น สัญลักษณ์ของความแปรปรวนประชากรคือ sigma กำลังสอง (σ ² ) และสัญลักษณ์ของความแปรปรวนตัวอย่างคือ s กำลังสอง (s ² )

นอกจากนี้ แนวคิดเรื่องค่าเบี่ยงเบนมาตรฐานและความแปรปรวนมีการตีความที่คล้ายกัน เนื่องจากทั้งสองค่าแสดงการกระจายตัวของชุดข้อมูลทางสถิติ

คุณสมบัติของส่วนเบี่ยงเบนมาตรฐาน (หรือส่วนเบี่ยงเบนมาตรฐาน)

ค่าเบี่ยงเบนมาตรฐานมีคุณสมบัติดังต่อไปนี้:

ค่าเบี่ยงเบนมาตรฐานของตัวอย่างข้อมูลไม่สามารถเป็นค่าลบได้

$\sigma \ge 0$

ค่าเบี่ยงเบนมาตรฐานจะเป็นศูนย์หากข้อมูลทั้งหมดเหมือนกัน

$\sigma =0$

หากมีการเพิ่มคำศัพท์คงที่ลงในข้อมูลทั้งหมด ค่าเบี่ยงเบนมาตรฐานจะไม่เปลี่ยนแปลง

$\sigma (X+k)=\sigma (X)$

หากข้อมูลทั้งหมดคูณด้วยตัวเลข ค่าเบี่ยงเบนมาตรฐานจะคูณด้วยค่าสัมบูรณ์ของตัวเลขดังกล่าว

$\sigma (k\cdot X)=|k|\cdot \sigma (X)$

ค่าเบี่ยงเบนมาตรฐานของผลรวมของตัวแปรสุ่มสองตัวจะเท่ากับรากที่สองของผลรวมของความแปรปรวนของตัวแปร บวก สองเท่าของความแปรปรวนร่วมระหว่างตัวแปรทั้งสอง

$\sigma(X+Y)=\sqrt{Var(X)+Var(Y)+2\cdot Cov(X,Y)}$

หากเราทราบค่าเบี่ยงเบนมาตรฐานของการแจกแจงที่แตกต่างกัน (σ _i ) และจำนวนข้อมูล (n _i ) เราสามารถคำนวณค่าเบี่ยงเบนมาตรฐานทั้งหมดได้โดยใช้สูตรต่อไปนี้:

$\displaystyle\sigma=\sqrt{\frac{\displaystyle \sum_{i=1}^N n_i\cdot \sigma_i^2}{\displaystyle \sum_{i=1}^N n_i}}=\sqrt{\frac{\displaystyle n_1\cdot \sigma_1^2+n_2\cdot \sigma_2^2+\dots +n_N\cdot \sigma_N^2}{\displaystyle n_1+n_2+\dots+n_N}}$

เกี่ยวกับผู้แต่ง

ดร.เบนจามิน แอนเดอร์สัน

สวัสดี ฉันชื่อเบนจามิน ศาสตราจารย์สถิติเกษียณอายุแล้ว และผันตัวมาเป็นครูสอนสถิติโดยเฉพาะ ด้วยประสบการณ์และความเชี่ยวชาญที่กว้างขวางในสาขาสถิติ ฉันกระตือรือร้นที่จะแบ่งปันความรู้ของฉันเพื่อเสริมศักยภาพนักเรียนผ่าน Statorials. รู้เพิ่มเติม