วิธีดำเนินการถดถอยพหุนามใน python

การวิเคราะห์การถดถอยใช้เพื่อหาปริมาณความสัมพันธ์ระหว่างตัวแปรอธิบายตั้งแต่หนึ่งตัวขึ้นไปกับตัวแปรตอบสนอง

การวิเคราะห์การถดถอยประเภทที่พบบ่อยที่สุดคือ การถดถอยเชิงเส้นอย่างง่าย ซึ่งใช้เมื่อตัวแปรทำนายและตัวแปรตอบสนองมีความสัมพันธ์เชิงเส้น

อย่างไรก็ตาม บางครั้งความสัมพันธ์ระหว่างตัวแปรทำนายและตัวแปรตอบสนองอาจไม่เป็นเชิงเส้น

ตัวอย่างเช่น ความสัมพันธ์ที่แท้จริงอาจเป็นกำลังสอง:

หรืออาจเป็นลูกบาศก์:

ในกรณีเหล่านี้ เหมาะสมที่จะใช้ การถดถอยพหุนาม ซึ่งสามารถอธิบายความสัมพันธ์แบบไม่เชิงเส้นระหว่างตัวแปรได้

บทช่วยสอนนี้จะอธิบายวิธีการถดถอยพหุนามใน Python

ตัวอย่าง: การถดถอยพหุนามใน Python

สมมติว่าเรามีตัวแปรทำนาย (x) และตัวแปรตอบสนอง (y) ใน Python ต่อไปนี้:

 x = [2, 3, 4, 5, 6, 7, 7, 8, 9, 11, 12]
y = [18, 16, 15, 17, 20, 23, 25, 28, 31, 30, 29]

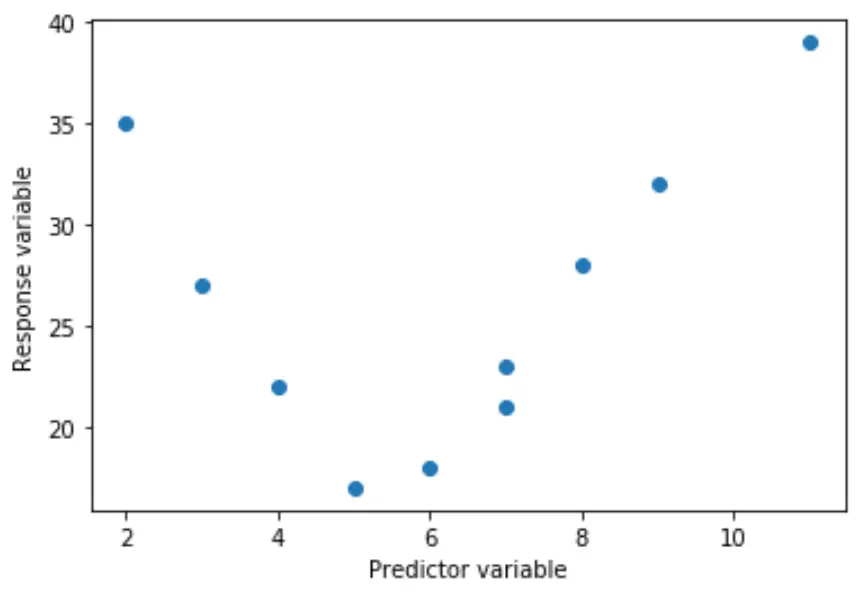
หากเราสร้างแผนภาพกระจายอย่างง่ายของข้อมูลนี้ เราจะเห็นว่าความสัมพันธ์ระหว่าง x และ y ไม่เป็นเชิงเส้นอย่างชัดเจน:

 import matplotlib.pyplot as plt

#create scatterplot 
plt.scatter(x, y)

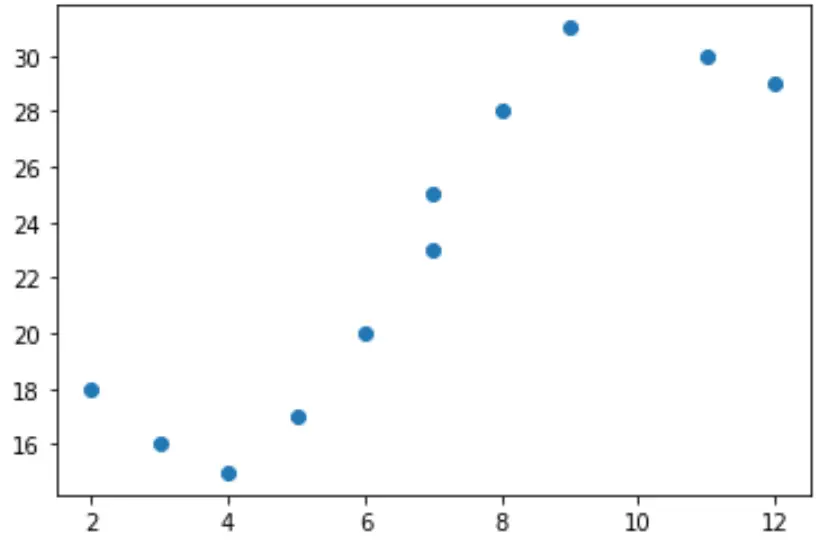
ดังนั้นจึงไม่เหมาะสมที่จะใส่แบบจำลองการถดถอยเชิงเส้นกับข้อมูลนี้ แต่เราสามารถพยายามปรับโมเดลการถดถอยพหุนามด้วยระดับ 3 ได้โดยใช้ฟังก์ชัน numpy.polyfit()

 import numpy as np

#polynomial fit with degree = 3
model = np.poly1d(np.polyfit(x, y, 3))

#add fitted polynomial line to scatterplot
polyline = np.linspace(1, 12, 50)
plt.scatter(x, y)
plt.plot(polyline, model(polyline))
plt.show() 

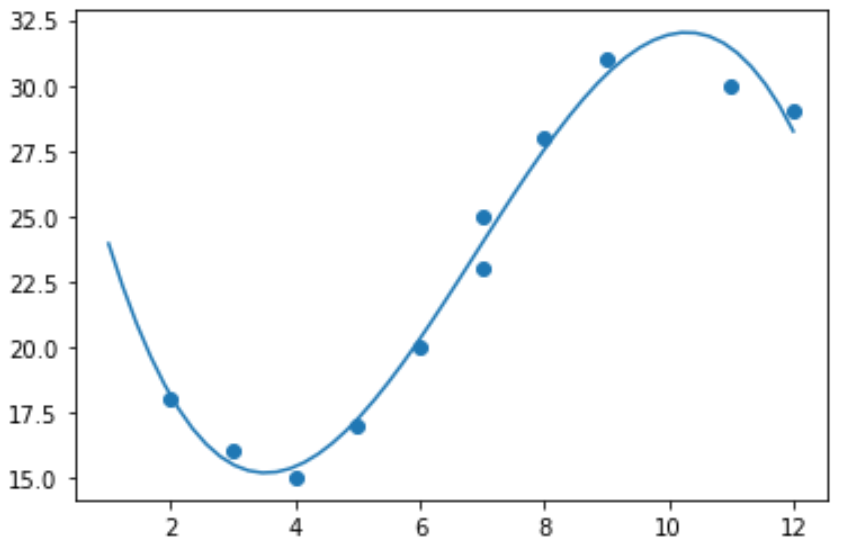
เราสามารถหาสมการถดถอยพหุนามพอดีได้โดยการพิมพ์ค่าสัมประสิทธิ์แบบจำลอง:

 print(model)

poly1d([ -0.10889554, 2.25592957, -11.83877127, 33.62640038])

สมการการถดถอยพหุนามพอดีคือ:

y = -0.109x ³ + 2.256x ² – 11.839x + 33.626

สมการนี้สามารถใช้เพื่อค้นหาค่าที่คาดหวังของตัวแปรตอบสนองโดยพิจารณาจากค่าที่กำหนดของตัวแปรอธิบาย

ตัวอย่างเช่น สมมติว่า x = 4 ค่าที่คาดหวังสำหรับตัวแปรตอบสนอง y จะเป็น:

y = -0.109(4) ³ + 2.256(4) ² – 11.839(4) + 33.626= 15.39 .

นอกจากนี้เรายังสามารถเขียนฟังก์ชันสั้นๆ เพื่อให้ได้ค่า R-squared ของแบบจำลอง ซึ่งเป็นสัดส่วนของความแปรปรวนในตัวแปรตอบสนองที่สามารถอธิบายได้ด้วยตัวแปรทำนาย

 #define function to calculate r-squared
def polyfit(x, y, degree):
    results = {}
    coeffs = numpy.polyfit(x, y, degree)
    p = numpy.poly1d(coeffs)
    #calculate r-squared
    yhat = p(x)
    ybar = numpy.sum(y)/len(y)
    ssreg = numpy.sum((yhat-ybar)**2)
    sstot = numpy.sum((y - ybar)**2)
    results['r_squared'] = ssreg / sstot

    return results

#find r-squared of polynomial model with degree = 3
polyfit(x, y, 3)

{'r_squared': 0.9841113454245183}

ในตัวอย่างนี้ ค่า R ของโมเดลคือ 0.9841

ซึ่งหมายความว่า 98.41% ของความแปรผันในตัวแปรตอบสนองสามารถอธิบายได้ด้วยตัวแปรทำนาย