วิธีการถดถอยลูกบาศก์ใน python
การถดถอยแบบลูกบาศก์ เป็นการถดถอยประเภทหนึ่งที่เราสามารถใช้เพื่อหาปริมาณความสัมพันธ์ระหว่างตัวแปรทำนายและตัวแปรตอบสนอง เมื่อความสัมพันธ์ระหว่างตัวแปรไม่เป็นเชิงเส้น
บทช่วยสอนนี้จะอธิบายวิธีการถดถอยลูกบาศก์ใน Python
ตัวอย่าง: การถดถอยลูกบาศก์ใน Python
สมมติว่าเรามี DataFrame แพนด้าต่อไปนี้ซึ่งมีตัวแปรสองตัว (x และ y):
import pandas as pd #createDataFrame df = pd. DataFrame ({' x ': [6, 9, 12, 16, 22, 28, 33, 40, 47, 51, 55, 60], ' y ': [14, 28, 50, 64, 67, 57, 55, 57, 68, 74, 88, 110]}) #view DataFrame print (df) xy 0 6 14 1 9 28 2 12 50 3 16 64 4 22 67 5 28 57 6 33 55 7 40 57 8 47 68 9 51 74 10 55 88 11 60 110
หากเราสร้างแผนภาพกระจายอย่างง่ายของข้อมูลนี้ เราจะเห็นว่าความสัมพันธ์ระหว่างตัวแปรทั้งสองนั้นไม่เป็นเชิงเส้น:
import matplotlib. pyplot as plt
#create scatterplot
plt. scatter (df. x , df. y )
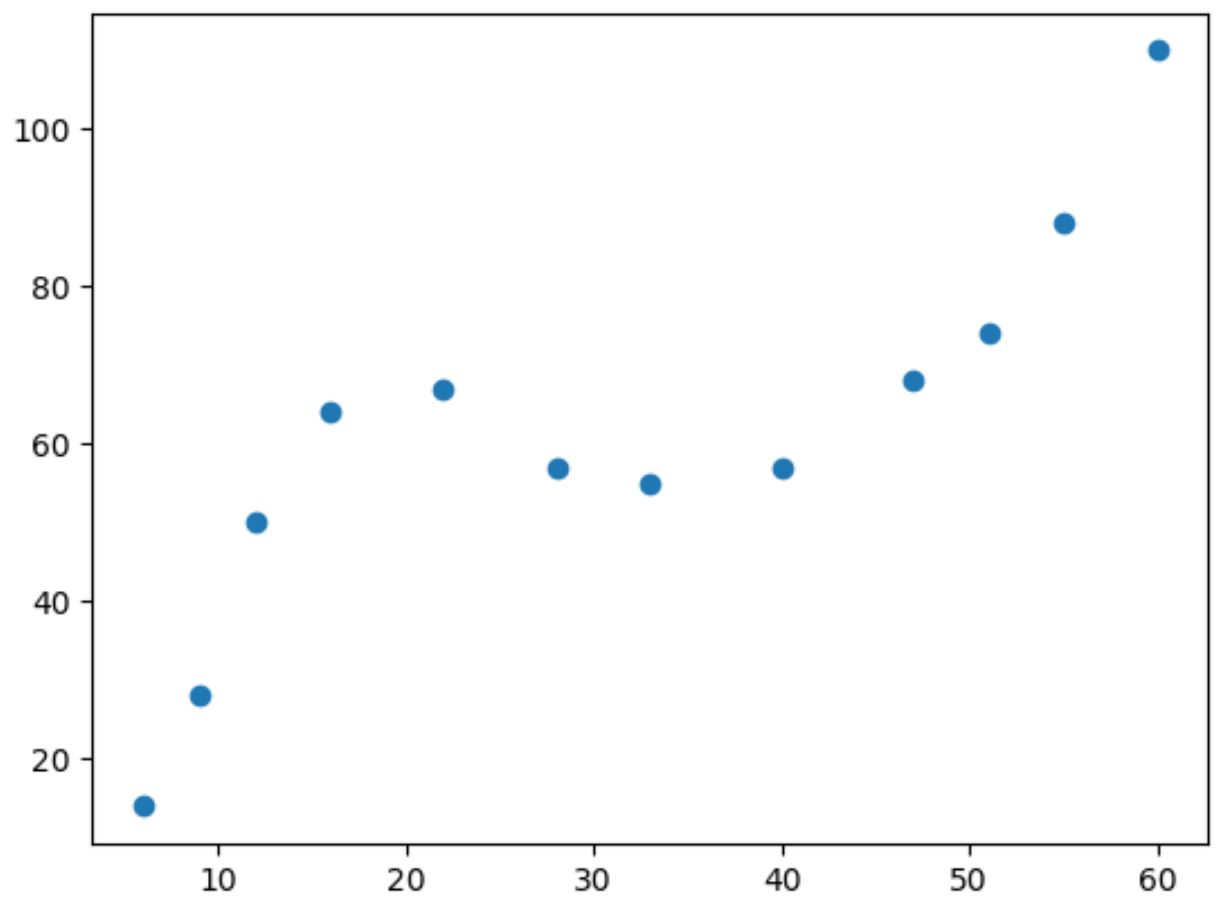
เมื่อค่า x เพิ่มขึ้น y จะเพิ่มขึ้นถึงจุดหนึ่ง จากนั้นลดลง แล้วจึงเพิ่มขึ้นอีกครั้ง
รูปแบบที่มี “เส้นโค้ง” สองเส้นในพล็อตนี้บ่งบอกถึงความสัมพันธ์แบบลูกบาศก์ระหว่างตัวแปรทั้งสอง
ซึ่งหมายความว่าแบบจำลองการถดถอยลูกบาศก์เป็นตัวเลือกที่ดีในการหาความสัมพันธ์ระหว่างตัวแปรทั้งสอง
ในการดำเนินการถดถอยลูกบาศก์ เราสามารถใส่แบบจำลองการถดถอยพหุนามที่มีระดับ 3 ได้โดยใช้ ฟังก์ชัน numpy.polyfit() :
import numpy as np #fit cubic regression model model = np. poly1d (np. polyfit (df. x , df. y , 3)) #add fitted cubic regression line to scatterplot polyline = np. linspace (1, 60, 50) plt. scatter (df. x , df. y ) plt. plot (polyline, model(polyline)) #add axis labels plt. xlabel (' x ') plt. ylabel (' y ') #displayplot plt. show ()
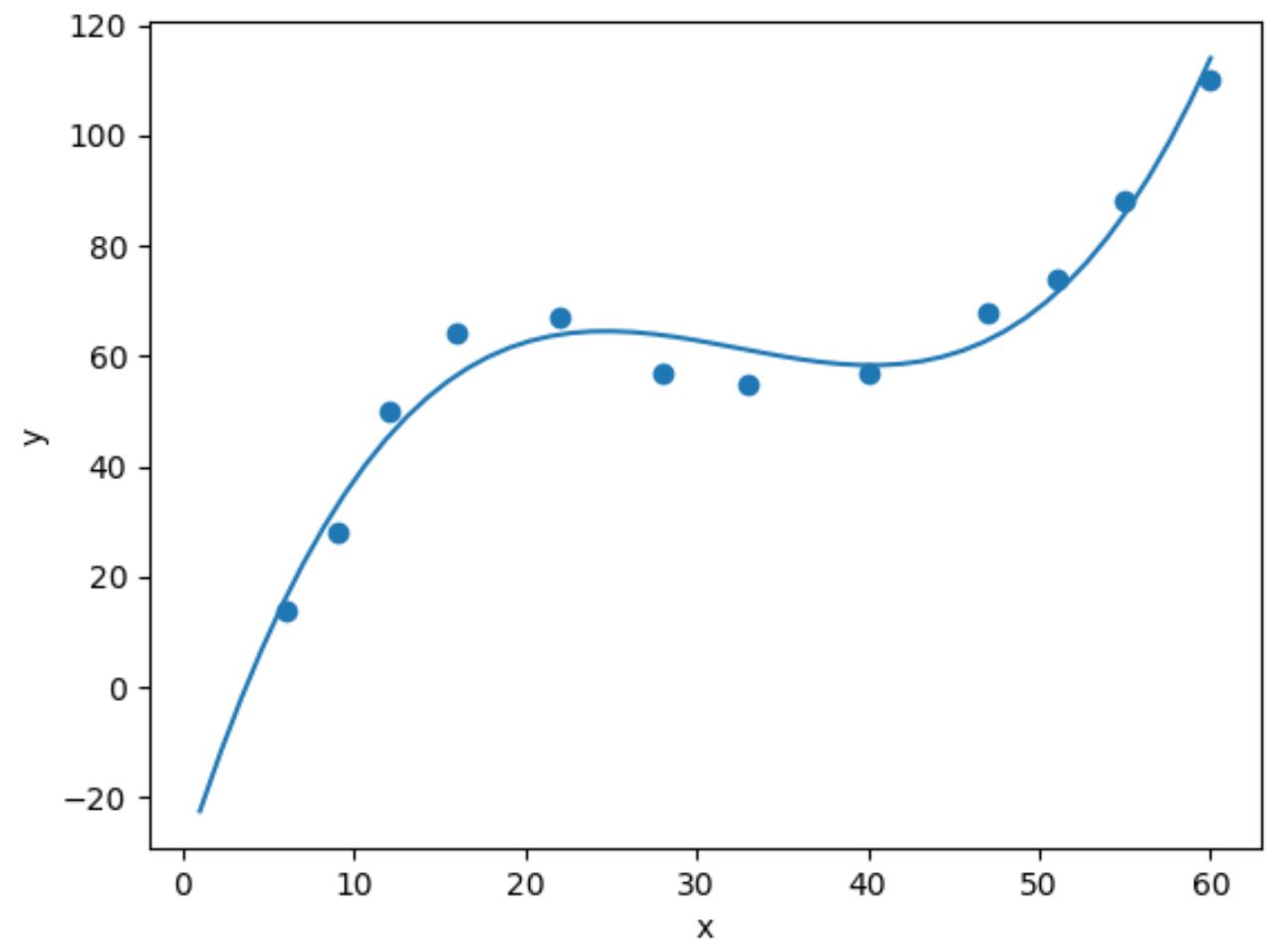
เราสามารถหาสมการถดถอยลูกบาศก์พอดีได้โดยการพิมพ์ค่าสัมประสิทธิ์แบบจำลอง:
print (model)
3 2
0.003302x - 0.3214x + 9.832x - 32.01
สมการถดถอยลูกบาศก์พอดีคือ:
y = 0.003302(x) 3 – 0.3214(x) 2 + 9.832x – 30.01
เราสามารถใช้สมการนี้เพื่อคำนวณค่าที่คาดหวังของ y ตามค่าของ x
ตัวอย่างเช่น ถ้า x คือ 30 ค่าที่คาดหวังสำหรับ y คือ 64.844:
y = 0.003302(30) 3 – 0.3214(30) 2 + 9.832(30) – 30.01 = 64.844
นอกจากนี้เรายังสามารถเขียนฟังก์ชันสั้นๆ เพื่อให้ได้ค่า R-squared ของแบบจำลอง ซึ่งเป็นสัดส่วนของความแปรปรวนในตัวแปรตอบสนองที่สามารถอธิบายได้ด้วยตัวแปรทำนาย
#define function to calculate r-squared def polyfit(x, y, degree): results = {} coeffs = np. polyfit (x, y, degree) p = np. poly1d (coeffs) #calculate r-squared yhat = p(x) ybar = np. sum (y)/len(y) ssreg = np. sum ((yhat-ybar) ** 2) sstot = np. sum ((y - ybar) ** 2) results[' r_squared '] = ssreg / sstot return results #find r-squared of polynomial model with degree = 3 polyfit(df. x , df. y , 3) {'r_squared': 0.9632469890057967}
ในตัวอย่างนี้ ค่า R ของโมเดลคือ 0.9632
ซึ่งหมายความว่า 96.32% ของความแปรผันในตัวแปรตอบสนองสามารถอธิบายได้ด้วยตัวแปรทำนาย
เนื่องจากค่านี้สูงมาก จึงบอกเราว่าแบบจำลองการถดถอยลูกบาศก์หาปริมาณความสัมพันธ์ระหว่างตัวแปรทั้งสองได้ดี
ที่เกี่ยวข้อง: ค่า R-squared ที่ดีคืออะไร?
แหล่งข้อมูลเพิ่มเติม
บทช่วยสอนต่อไปนี้จะอธิบายวิธีทำงานทั่วไปอื่นๆ ใน Python:
วิธีดำเนินการถดถอยเชิงเส้นอย่างง่ายใน Python
วิธีดำเนินการถดถอยกำลังสองใน Python
วิธีดำเนินการถดถอยพหุนามใน Python