รหัส Python แบบเต็มที่ใช้ในบทช่วยสอนนี้สามารถพบได้ ที่นี่
วิธีการดำเนินการถดถอยโลจิสติกใน python (ทีละขั้นตอน)
การถดถอยแบบลอจิสติก เป็นวิธีการที่เราสามารถใช้เพื่อให้พอดีกับแบบจำลองการถดถอยเมื่อ ตัวแปรตอบสนอง เป็นไบนารี
การถดถอยโลจิสติกใช้วิธีการที่เรียกว่า การประมาณค่าความน่าจะเป็นสูงสุด เพื่อค้นหาสมการในรูปแบบต่อไปนี้:
บันทึก[p(X) / ( 1 -p(X))] = β 0 + β 1 X 1 + β 2 X 2 + … + β พี
ทอง:
- X j : ตัวแปร ทำนายที่ j
- β j : การประมาณค่าสัมประสิทธิ์ของตัวแปรทำนายที่ j
สูตรทางด้านขวาของสมการทำนาย อัตราต่อรองของบันทึก ที่ตัวแปรตอบกลับรับค่า 1
ดังนั้น เมื่อเราปรับแบบจำลองการถดถอยลอจิสติกให้เหมาะสม เราสามารถใช้สมการต่อไปนี้เพื่อคำนวณความน่าจะเป็นที่การสังเกตที่กำหนดจะได้ค่า 1:
p(X) = อี β 0 + β 1 X 1 + β 2 X 2 + … + β p
จากนั้นเราใช้เกณฑ์ความน่าจะเป็นที่แน่นอนเพื่อจัดประเภทการสังเกตเป็น 1 หรือ 0
ตัวอย่างเช่น เราสามารถพูดได้ว่าการสังเกตที่มีความน่าจะเป็นมากกว่าหรือเท่ากับ 0.5 จะถูกจัดประเภทเป็น “1” และการสังเกตอื่นๆ ทั้งหมดจะถูกจัดประเภทเป็น “0”
บทช่วยสอนนี้ให้ตัวอย่างทีละขั้นตอนของวิธีการดำเนินการถดถอยโลจิสติกใน R
ขั้นตอนที่ 1: นำเข้าแพ็คเกจที่จำเป็น
ขั้นแรก เราจะนำเข้าแพ็คเกจที่จำเป็นเพื่อทำการถดถอยโลจิสติกใน Python:
import pandas as pd import numpy as np from sklearn. model_selection import train_test_split from sklearn. linear_model import LogisticRegression from sklearn import metrics import matplotlib. pyplot as plt
ขั้นตอนที่ 2: โหลดข้อมูล
สำหรับตัวอย่างนี้ เราจะใช้ชุดข้อมูล เริ่มต้น จาก หนังสือ Introduction to Statistical Learning เราสามารถใช้โค้ดต่อไปนี้เพื่อโหลดและแสดงข้อมูลสรุปของชุดข้อมูล:
#import dataset from CSV file on Github url = "https://raw.githubusercontent.com/Statorials/Python-Guides/main/default.csv" data = pd. read_csv (url) #view first six rows of dataset data[0:6] default student balance income 0 0 0 729.526495 44361.625074 1 0 1 817.180407 12106.134700 2 0 0 1073.549164 31767.138947 3 0 0 529.250605 35704.493935 4 0 0 785.655883 38463.495879 5 0 1 919.588530 7491.558572 #find total observations in dataset len( data.index ) 10000
ชุดข้อมูลนี้มีข้อมูลต่อไปนี้เกี่ยวกับบุคคล 10,000 คน:
- ค่าเริ่มต้น: ระบุว่าบุคคลนั้นผิดนัดหรือไม่
- นักเรียน: ระบุว่าบุคคลนั้นเป็นนักเรียนหรือไม่
- ยอดคงเหลือ: ยอดคงเหลือเฉลี่ยที่ถือโดยบุคคล
- รายได้: รายได้ของแต่ละบุคคล
เราจะใช้สถานะนักศึกษา ยอดคงเหลือในธนาคาร และรายได้เพื่อสร้างแบบจำลองการถดถอยลอจิสติกที่คาดการณ์ความน่าจะเป็นที่บุคคลหนึ่งๆ จะผิดนัดชำระหนี้
ขั้นตอนที่ 3: สร้างตัวอย่างการฝึกอบรมและการทดสอบ
ต่อไป เราจะแบ่งชุดข้อมูลออกเป็นชุดการฝึกเพื่อ ฝึก โมเดลและชุดทดสอบ เพื่อทดสอบ โมเดล
#define the predictor variables and the response variable X = data[[' student ',' balance ',' income ']] y = data[' default '] #split the dataset into training (70%) and testing (30%) sets X_train,X_test,y_train,y_test = train_test_split (X,y,test_size=0.3,random_state=0)
ขั้นตอนที่ 4: ติดตั้งแบบจำลองการถดถอยโลจิสติก
ต่อไป เราจะใช้ฟังก์ชัน LogisticRegression() เพื่อให้พอดีกับแบบจำลองการถดถอยโลจิสติกกับชุดข้อมูล:
#instantiate the model log_regression = LogisticRegression() #fit the model using the training data log_regression. fit (X_train,y_train) #use model to make predictions on test data y_pred = log_regression. predict (X_test)
ขั้นตอนที่ 5: การวินิจฉัยโมเดล
เมื่อเราติดตั้งแบบจำลองการถดถอยแล้ว เราก็จะสามารถวิเคราะห์ประสิทธิภาพของแบบจำลองของเราบนชุดข้อมูลทดสอบได้
ขั้นแรก เราจะสร้างเมทริกซ์ความสับสน สำหรับโมเดล:
cnf_matrix = metrics. confusion_matrix (y_test, y_pred)
cnf_matrix
array([[2886, 1],
[113,0]])
จากเมทริกซ์ความสับสนเราจะเห็นได้ว่า:
- #คำทำนายเชิงบวกที่แท้จริง: 2886
- #คำทำนายเชิงลบที่แท้จริง: 0
- #คำทำนายผลบวกลวง : 113
- #การทำนายเชิงลบที่เป็นเท็จ: 1
นอกจากนี้เรายังสามารถรับแบบจำลองความแม่นยำ ซึ่งบอกเปอร์เซ็นต์ของการคาดการณ์การแก้ไขที่ทำโดยแบบจำลอง:
print(" Accuracy: ", metrics.accuracy_score (y_test, y_pred))l
Accuracy: 0.962
ข้อมูลนี้บอกเราว่าโมเดลคาดการณ์ได้ถูกต้องว่าบุคคลนั้นจะผิดนัด 96.2% ของเวลาหรือไม่
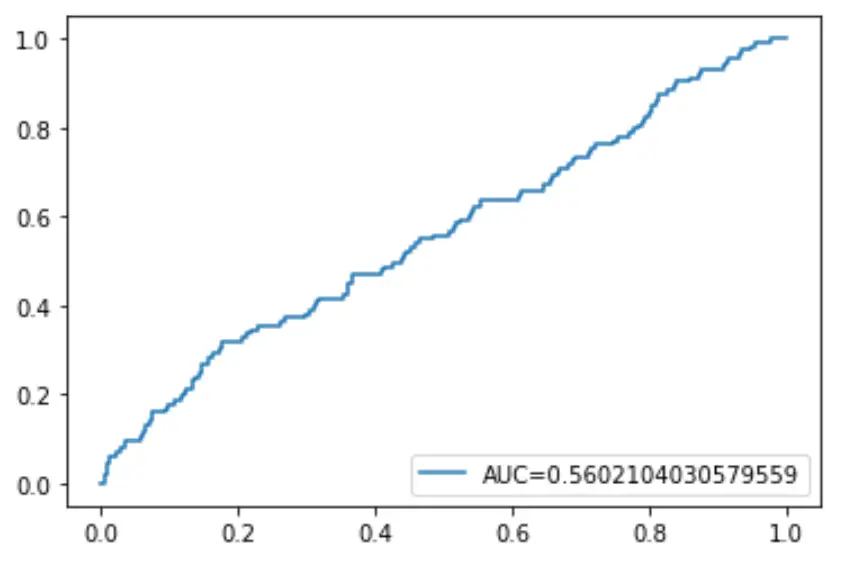
สุดท้ายนี้ เราสามารถพล็อตเส้นโค้งลักษณะการทำงานของตัวรับ (ROC) ซึ่งแสดงเปอร์เซ็นต์ของผลบวกจริงที่ทำนายโดยแบบจำลอง เมื่อเกณฑ์ความน่าจะเป็นในการทำนายลดลงจาก 1 เป็น 0
ยิ่ง AUC สูง (พื้นที่ใต้เส้นโค้ง) แบบจำลองของเราก็สามารถทำนายผลลัพธ์ได้แม่นยำยิ่งขึ้น:
#define metrics
y_pred_proba = log_regression. predict_proba (X_test)[::,1]
fpr, tpr, _ = metrics. roc_curve (y_test, y_pred_proba)
auc = metrics. roc_auc_score (y_test, y_pred_proba)
#create ROC curve
plt. plot (fpr,tpr,label=" AUC= "+str(auc))
plt. legend (loc=4)
plt. show ()